ArrayDeque源码学习

前置知识

为了更好的理解使用线性数组实现的双端队列，这里我们先来图解线性数组实现基本数据结构-队列：

如上图所示，head指向队头，入队加元素时，tail队尾向后移动，出队时从head出取出元素并移除，这样就利用了线性数组实现先进先出的队列数据结构，当head等于tail时，则表示队列为空。
但是这样存在问题：当不断出队时，head向后移动，前面空出来的空间就被浪费，导致不断入队时，需要数组扩容，出队时造成大量空间无法使用，空间利用率低下！
假设，如果能将前面空出来的空间也利用起来进行存储末尾的元素，则空间使用率将提高，这里就需要有个循环的思维，把这种线性的弯曲成一个圆环，这样就可以反复使用空出来的空间，入队时使用出队空余出来的空间，就解决以上的问题，图解如下：

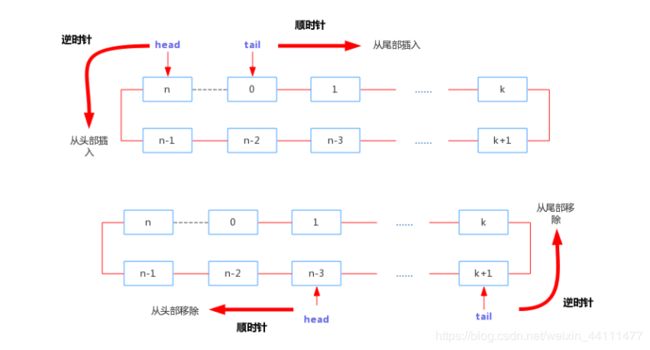
同样，当head等于tail时，则表示循环队列为空。head和tail也是循环的，像钟表中的时针，具有周期性。这里head和tail需要对长度lenth取模，这样head和tail将一直在长度范围内，可以作为数组的下标。

对于如何将数据分布到相应大小的连续空间中，常用的方式就是取模运算，即position=index%len，利用整数倍的周期性，将剩余的部分作为空间索引。

基本定义

ArrayDeque是JDK容器中的一个双端队列实现，内部使用数组进行元素存储，不允许存储null值，可高效的进行元素查找和尾部插入取出，是用作队列、双端队列、栈的绝佳选择，性能比LinkedList还要好的构造方法。

• 基本属性定义如下:

 //存储元素的数组
   transient Object[] elements; // 非private访问限制，以便内部类访问
    
    // 头部节点序号，相当于头指针
    transient int head;

    // 尾部节点序号，（下一个插入的元素的位置），相当于尾指针
    transient int tail;
    
    // 双端队列的最小容量，必须是2的幂
    private static final int MIN_INITIAL_CAPACITY = 8;

构造方法

	//构造一个初始容量为16的空队列
	public ArrayDeque() {
        elements = new Object[16];
    }
    //构造一个能容纳指定大小的空队列
    public ArrayDeque(int numElements) {
        allocateElements(numElements);
    }
    //构造一个包含指定集合所有元素的队列
    public ArrayDeque(Collection<? extends E> c) {
        allocateElements(c.size());
        addAll(c);
    }

核心方法

1、分配元素

在上述第二与第三个构造方法中，里面调用allocateElements()，让我们来看看它的实现：

	public ArrayDeque(int numElements) {
        allocateElements(numElements);
    }
    
    private void allocateElements(int numElements) {
        int initialCapacity = MIN_INITIAL_CAPACITY;
        // 找到一个能满足刚好大于指定长度的2次幂数
            if (numElements >= initialCapacity) {
            initialCapacity = numElements;
            initialCapacity |= (initialCapacity >>>  1);
            initialCapacity |= (initialCapacity >>>  2);
            initialCapacity |= (initialCapacity >>>  4);
            initialCapacity |= (initialCapacity >>>  8);
            initialCapacity |= (initialCapacity >>> 16);
            initialCapacity++;
            
			//当n已经为2^31时，左移一位会造成溢出，即将数据最高位的1移动到符号位上，这样会变负
            if (initialCapacity < 0)   // 过度扩容，需要减容一次
                initialCapacity >>>= 1;// Good luck allocating 2 ^ 30 elements
        }
        elements = new Object[initialCapacity];
    }

allocateElements方法主要用于给内部的数组分配合适大小的空间，calculateSize方法用于计算比numElements大的最小2的幂次方，如果指定的容量大小小于MIN_INITIAL_CAPACITY（值为8），那么将容量设置为8，否则通过多次无符号右移进行最小2次幂计算。先将initialCapacity赋值为numElements，接下来，进行5次无符号右移，下面将以一个例子介绍这样运算的妙处。
在Java中，int类型是占4字节，也就是32位。简单起见，这里以一个8位二进制数来演示前三次操作。假设这个二进制数对应的十进制为89，整个过程如下：

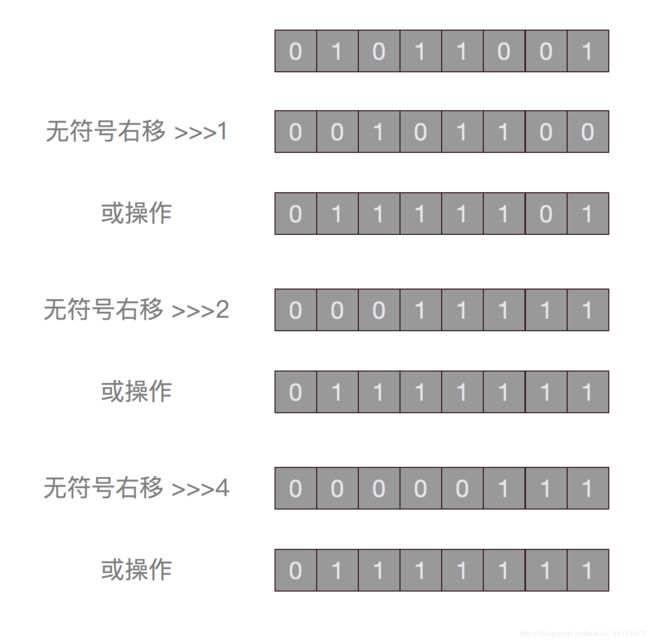
事实上，在这系列操作中，其他位只是配角，我们只需要关注第一个不为0的位即可，假设其为第n位，先右移一位然后进行或操作，得到的结果，第n位和第n-1位肯定为1，这样就有两个位为1了，然后进行右移两位，再进行或操作，那么第n位到第n-3位一定都为1，然后右移4位，依次类推。int为32位，因此，最后只需要移动16位即可。1+2+4+8+16 = 31，所以经过这一波操作，原数字对应的二进制，操作得到的结果将是从其第一个不为0的位开始，往后的位均为1。

2、扩容

当头指针和尾指针指向同一位置，即该双向队列满的时候，调用doubleCapacity()方法。

	private void doubleCapacity() {
		//断言头指针和尾指针指向同一位置时，继续执行该方法
        assert head == tail;
        int p = head;
        int n = elements.length;
        //获取到头指针右部剩余的元素个数
        int r = n - p; 
        //将该队列做无符号左移一位，容量扩大一倍
        int newCapacity = n << 1;
        //当n已经为2^31时，左移一位会造成溢出，即将数据最高位的1移动到符号位上，这样会变负
        if (newCapacity < 0)
            throw new IllegalStateException("Sorry, deque too big");
        //创建一个临时数组对象，长度为newCapacity
        Object[] a = new Object[newCapacity];
        /* 
        1、将数组elements的头指针开始的元素，快速拷贝到数组a中下标为0的位置,长度为r 
        2、将数组elements的0下标开始的元素，快速拷贝到数组a中下标为r的位置,长度为p
        这样使得头指针前的元素（实际上是尾部的元素）移回到该有数组尾部的位置，相当于恢复到头指针指向尾指针，长度为原本容量
        */
        System.arraycopy(elements, p, a, 0, r);
        System.arraycopy(elements, 0, a, r, p);
        elements = a;
        //将头指针指向数组的首部
        head = 0;
         //将尾指针指向扩容后数据的最尾端
        tail = n;
    }

3、 添加

	public boolean add(E e) {
        addLast(e);
        return true;
    }

	public void addLast(E e) {
		//ArrayDeque不允许元素为null值
        if (e == null)
            throw new NullPointerException();
        //将添加元素存入队列下标为tail的位置中
        elements[tail] = e;
        //更新尾指针的节点序号,如果尾指针与头指针相同,则说明需要扩容
        if ( (tail = (tail + 1) & (elements.length - 1)) == head)
            doubleCapacity();
    }
	
	public void addFirst(E e) {
		//ArrayDeque不允许元素为null值
        if (e == null)
            throw new NullPointerException();
        //更新头指针的节点序号
        elements[head = (head - 1) & (elements.length - 1)] = e;
        //如果尾指针与头指针相同，则说明需要扩容
        if (head == tail)
            doubleCapacity();
    }

(tail = (tail + 1) & (elements.length - 1)) == head -> 在 ArrayDeque 中数组是当作环形来使用的，索引0看作是紧挨着索引(length-1)之后的。参考下面的图片：

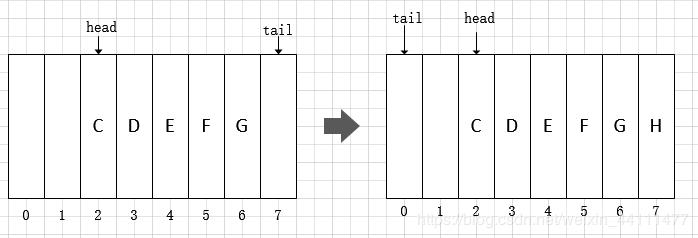
那么为什么(tail + 1) & (elements.length - 1)就能保证按照环形取得正确的下一个索引值呢？这就和前面说到的 ArrayDeque 对容量的特殊要求有关了。下面对其正确性加以验证：

length     = 2^n     ，二进制表示为: 第 n 位为1，低位 (n-1位)全为0 
length - 1 = 2^n-1，二进制表示为：第 n 位为0 ，低位(n-1位)全为1              （始终保持）
    
若 tail + 1 <= length - 1 ，则位与后，低 (n-1) 位保持不变，高位全为0
若 tail + 1  = length     ，则位与后，低 n 全为0，高位也全为0，结果为0

可见，在容量保证为 2^n 的情况下，仅仅通过位与操作就可以完成环形索引的计算，而不需要进行边界的判断，在实现上更为高效。

引用资料

1、https://www.cnblogs.com/mfrank/p/9600137.html
2、https://www.cnblogs.com/wxd0108/p/7366234.html
3、https://www.cnblogs.com/lxyit/p/9080590.html