全波形反演
目标:利用岩土地震数据的弹性FWI改进地下特征,以用于岩土、水文地质应用。开发用于浅层地震数据反演的新技术,将致力于提高FWI代码IFOS2D的效率和可靠性。
Chapter 1 Introduction
全波形反演(FWT)的目的是估计地下弹性材料的参数。这可以通过使用梯度优化方法最小化建模数据和现场数据之间的不匹配能量来实现。由于FWT利用每个地震记录的全部信息内容,可以解决地震波以下的结构问题。与 travel time tomography相比,这在分辨率上有了巨大的提高。
全波形反演指利用非线性寻优方法反演给定时窗内的波形记录以获取影响地震波传播的相关物性参数(如弹性参数、粘弹性参数、各向异性参数、密度等)的方法。
通俗地讲,全波形反演就是利用波场模拟和实际地震资料对比,通过多次迭代使预测波场和实际地震资料匹配一致,求取地下地质参数用于构造成像与储层综合研究的一种地震反演方法。
为了从地震观测中提取有关地壳结构和成分的信息,必须能够预测地震波场如何受到复杂结构的影响。由于大多数地下结构不存在波动方程的精确解析解,因此只能通过数值方法获得解。对于有限计算机资源的合成地震记录迭代计算,需要快速、准确的建模方法。
IFOS2D(全观测地震图的反演)基于Virieux[1986]和Levander[1988]描述的FD方法。本程序IFOS2D具有以下扩展:
•利用MPI进行区域分解,
•考虑了弹性波传播效应、衰减和色散,
•使用高阶FD算子
•在数值网格边缘应用卷积完全匹配的层边界条件
IFOS基本思路:
目的:从地震波形中提取出有关地壳结构和成分信息
=>明确地壳结构和地震波场之间的关系(利用波动方程)
=>求解波动方程,得到解析解或数值解,获得弹性位移场ui(xs,xr,t)的关系
=>迭代材料的弹性参数,解得不同的位移场,与真实地震数据比较,直到找到具有最小残差的最优模型
Chapter2 The oretical Background
2.1 弹性介质的运动方程
一般弹性介质中的波的传播可以用一组线性或部分微分方程来描述。它们由运动方程组成:
简单地说,介质的动量,密度ρ和位移速度vi的乘积,可以由表面力改变,表面力用应力张量σij或体积力(??不确定)fi来描述。这些方程描述了一般的介质,如玻璃、液体、固体质。材料特性由附加方程介绍,该方程描述了当施加一定的力时,介质如何反应。在各向同性弹性情况下,这可以用线性应力应变关系来描述:

式中,λ和μ是Lam’e参数,![]() 是应变张量,ui是位移。使用vi=∂ui/∂t,(2.1)和(2.2)可转换为二阶偏微分方程组:
是应变张量,ui是位移。使用vi=∂ui/∂t,(2.1)和(2.2)可转换为二阶偏微分方程组:

这种公式称为压力置换公式。利用式(2.3)中应力-应变关系和应变张量的时间导数,可以推导出运动弹性方程的另一种常见形式。由于Lam’e参数λ和μ不依赖于时间,公式(2.3)可以写成:
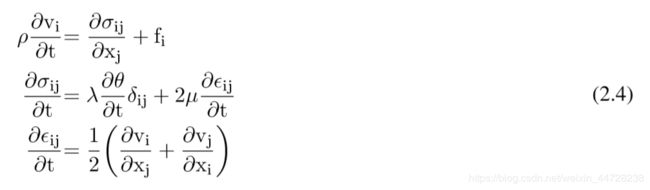
这个表达式叫做应力速度公式。对于简单的情况(2.3)和(2.4),可以用解析法求解。更复杂的问题需要数值解。下一节将介绍数值解的一种可能方法。
总的来说,各向异性弹性波方程能够更加准确地描述实际地震波传播的动力学特征。
IFOS2D对一组三个弹性参数(这里是两个Lame参数和密度)来对波形进行反演。通过确定不同的弹性参数来推导出不同的波场,直到与真实的地震波形的相同。(???不确定)
2.2 用微分法求解弹性波方程
对于弹性运动方程的数值解,方程组。(2.3)必须在时间和空间网格上离散化。在离散笛卡尔坐标x=i dh,y=j dh和离散时间t=n dt下,计算并定义颗粒速度v、应力σij、Lam’e参数λ和μ。dh表示两个相邻网格点之间的空间距离,dt表示两个连续时间步之间的差。因此,每个网格点都位于区间i∈N |[1,NX]、j∈N |[1,NY]和n∈N |[1,NT]中,其中NX、NY和NT分别是离散空间网格点和时间步数。最后用有限差分(FD)算子代替偏导数。可以区分两种类型的运算符,前向运算符和后向运算符D+,D-。函数y相对于变量x的导数可由以下运算符近似:

为了计算波场变量在正确位置的空间导数,这些变量不是放置在同一网格点上,而是交错放置在空间网格点距离的一半(Virieux[1986]和Levander[1988])。图2.1显示了材料参数和波场变量在空间网格上的分布。
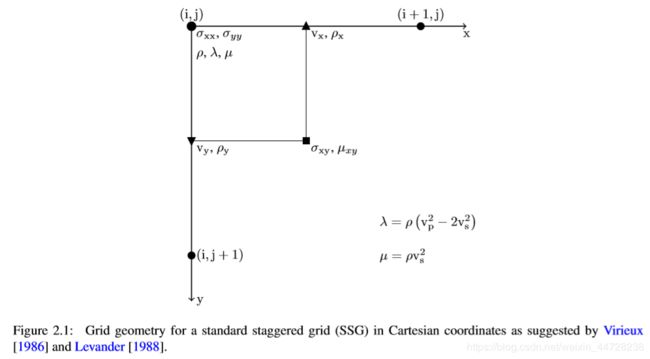
为了保证标准交错网格(SSG)代码的稳定性,必须对Lam’e参数μ和密度ρ进行调和和算术平均

在时间步骤n,将(2.4)中的线性应力-速度关系离散化,得到以下方程组:
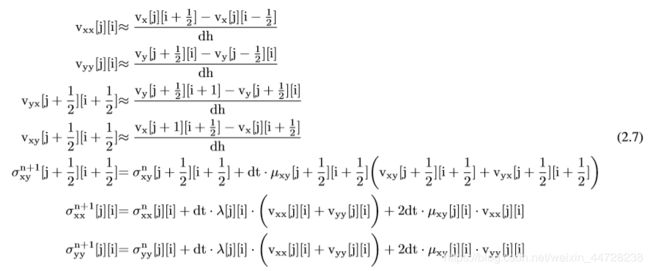
(2.4)中动量方程的离散化导致以下方程组:

2.2.2 FD算子的精度
最后一节中FD算子的推导是用有限差分代替偏导数。在以下更系统的方法中,通过泰勒级数展开估计网格点i处变量f的第一阶导数(Jastram【1992】:

对于长度为2N的算子,N个方程加上权重βk:

情形N=1导致在最后一部分中导出的FD算子,其长度为2N=2。泰勒级数在第一项(O(dh)2)之后被截断。因此,该算子称为二阶FD算子,它是指泰勒级数的截断误差,而不是指近似导数的阶数。为了更好地理解方程(2.9),我们估计了一个4阶算子。此运算符的长度为2N=4或N=2。式(2.9)中的总和导致:
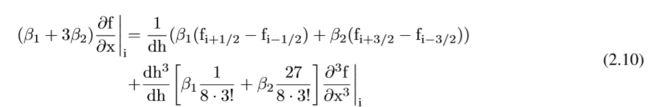
权重βk可通过以下方法计算:等式(2.10)的LHS偏导数前面的因子应等于1,因此![]()
(2.10)中 前面的系数应当消失
前面的系数应当消失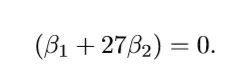
可通过求解矩阵方程来估计权重βk:
得到的系数为β1=9/8和β2=-1/24。因此,四阶后向和前向运算符是: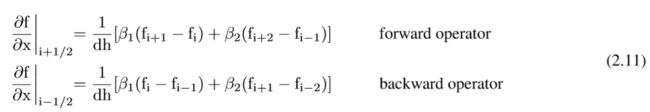
FD算子中的系数βi称为泰勒系数。可以通过寻找在一定频率范围内近似于一阶导数的FD系数βk来提高高阶导数的精确度(Holberg[1987])。这些数值优化系数称为霍尔伯格系数。
2.2.3 初始条件和边界条件
为了得到问题的唯一解,必须定义初始条件和边界条件。弹性前向问题的初始条件是:

对于所有的 x ∈ V,当 t = 0.时。
对于地球物理应用,两种边界条件非常重要:
1.水平自由面:当试图在海洋环境中模拟表面波或多个反射时,这些表面在最后一个和人类数据之间的界面非常重要。因为在这个界面的法向上的所有应力都消失了,所以

这种边界条件称为(应力)自由面。有两种实现是常见的。在自由曲面的含义中,空气声学参数(Vp=300 m/s,Vs=0.0 m/s,ρ=1.25 kg/m3)的所有图层都放置在模型顶部。自由表面隐式定义的一个优点是在FD网格上容易实现地形,但是为了获得表面波或多次波的精确结果,这种方法需要在自由表面附近对FD网格进行精确的空间采样。利用Levander的镜像技术可以实现显式自由面,从而得到平面界面的稳定精确解(Levander[1988],robertson等人。〔1995〕。如果平面自由面位于网格点j=h处,则该点的应力设置为零,自由面下方的应力镜像为反符号:

当更新自由表面上的应力分量σxx=dt(λ+2μ)vxx+dtλvyy时,只应使用水平粒子速度,因为自由表面上的垂直导数会导致不稳定性(Levander[1988])。在自由表面的边界条件下,可以放置速度vyy的垂直导数: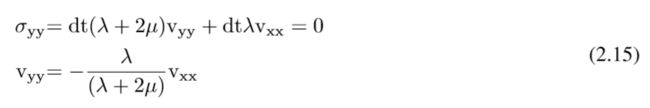
因此压力 σxx可以被写作:
2.吸收边界条件:由于有限的计算资源,FD网格必须尽可能小。为了模拟在不同方向上具有有限延伸的问题,例如全空间或半空间问题,必须应用艺术吸收边界条件。一种非常有效的方法是完全匹配层(PMLs)来阻尼边界附近的波。这可以通过频率域中波方程的坐标拉伸来实现(Komatitschmanartin[2007])。在吸收边界框架中,坐标拉伸产生六阶衰减平面波解。如果精确的波动方程得到求解,则PML是无反射的。一旦问题离散化(例如使用有限差分),您就可以解决近似的波动方程,并在不长时间有效的情况下进行分析完善。为了克服这个缺点,波场被阻尼函数阻尼
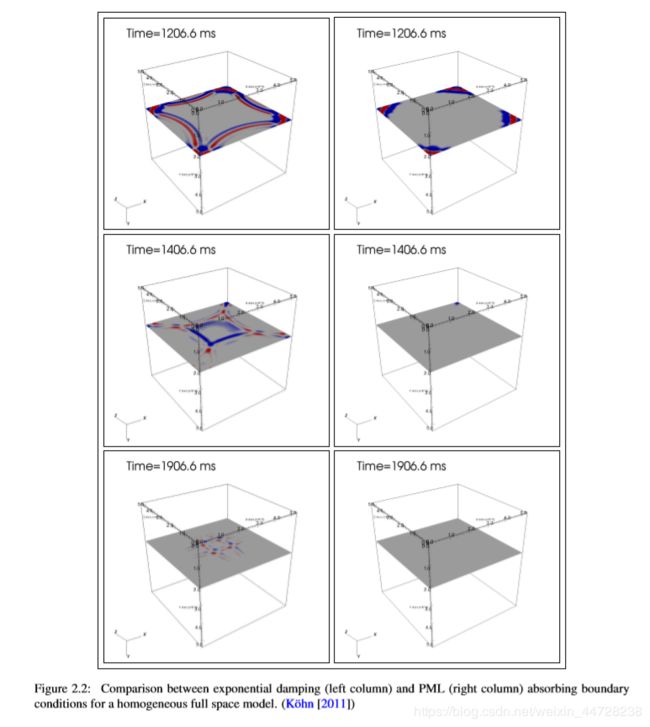
式中,Vpml表示吸收边界框架中介质的典型p波速度,α=1×10-4,L是吸收边界层的厚度。指数阻尼和PML边界之间的比较如图2.2所示。PMLs对地震波的阻尼比吸收边界框架有效5-10倍。
2.3 数值特性和不稳定性
为了在建模运行过程中避免数值放大和不稳定性,必须满足波场的空间和时间采样条件。以下两节将讨论这些问题。
2.3.1 网格离散
建立FD模型时的第一个问题是:对于波场的正确采样,最大空间网格点距离dh是多少?为了回答这个问题,我们看一个简单的例子:x方向的粒子位移由正弦函数定义
其中,λ表示波长。在x=0时解析计算该函数的导数,并设置λ=1 m时,我们得到:
在下一步中,通过交错二阶差分算子对推导进行数值逼近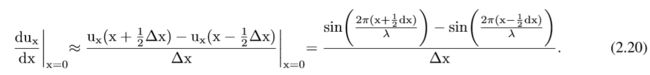
使用奈奎斯特-香农采样定理,应能充分利用∏x=λ/2对波场进行采样。在表2.1中,比较了公式(2.20)和解析解(2.19)在不同采样间隔∏x=λ/n下的数值解,其中n是每个波长的网格点数量。对于与Nyquist-Shannon定理相对应的n=2情形,数值解为dux dx | x=0=4.0,这与解析解2π不相等。对波场空间采样的重新定义可改善有限差分解。对于n=16,数值解精确到小数点后第二位。对于具有无应力表面的均质块体模型,图2.3说明了少量取样压力场的影响。FD网格的尺寸和源信号的中心频率系统地增加。当每最小波长(图2.3,顶部)使用16个网格点的空间采样时,波前会急剧减小。对于n=4个网格点,波有轻微的数值色散(图2.3,中心)。当使用奈奎斯特标准(n=2)时,这种效果是明显的(图2.3,底部)。由于数值计算的波场似乎是色散的,所以这种数值模拟被称为网格色散。为避免网格离散的发生,必须满足以下关于空间网格间距dh的标准:

这里,λmin表示最小波长,Vmin表示模型中的最小速度,fmax表示源信号的最大频率。根据所用FD算子的精度,参数n是不同的。表2.2中列出了不同FD算子长度和类型(Taylor算子和Holberg算子)的n。计算霍尔伯格系数时,3fmax处的最小色散误差为0.1%。对于较短的算子n应选择较大的,因此空间网格间距较小,而对于较长的FD算子n较小,网格间距可以较大。![]()


2.3.2 库兰特不稳定性
临时退出必须满足适用的资源稳定性标准。如果波在离散网格上传播,则时间步长dt必须小于波在具有网格间距dh的两个相邻网格点之间传播的时间。对于弹性二维网格,这在数学上意味着:

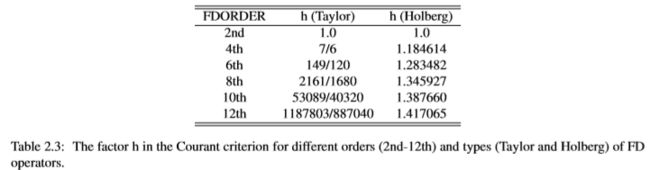
其中Vmax是模型中的最大速度。因子h取决于FD算子的阶数,并且可以通过加权系数βi的求和来方便地计算
![]()
表2.3中列出了不同FD算子长度和类型(Taylor算子和Holberg算子)的h。标准(2.22)称为Courant-Friedrichs-Lewy标准(Courant et al。[1928],Courant等人。[1967年3月])。图2.4显示了违反Courant准则时压力场的演变。经过几步时间后,振幅逐渐增大,计算变得不稳定。

Chapter3 The adjoint problem
全波形反演的目的是找到一个能很好解释数据的“最佳”模型。它不仅应解释地震波场折射或反射等特定相位的首次到达,还应解释包含地下弹性材料参数分布信息的振幅。要实现这一目标,必须解决三个问题:
1.什么是“最佳”模式?
2.怎么能找到这个模型?
3.这个模型是唯一的还是现有的其他模型,这些模型可以很好地解释数据?
3.1 What is an ”optimum” model?
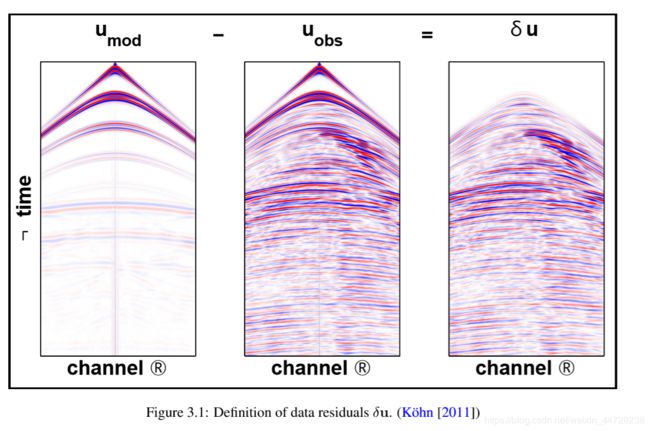
在反射地震中,由位于xs处的震源激发的弹性位移场ui(xs,xr,t)的第i个分量将由xr处的接收器在时间t处记录。对于给定的材料参数分布,可通过有限差分(第2.2节)解决正向问题等式2.3。结果是一个模型数据集umod。该建模数据可与现场数据uobs进行比较。如果建模数据和现场数据之间的误差或数据残差δu=umod-uobs(图3.1)很小,则模型可以很好地解释数据。如果残差很大,模型就不能解释数据。误差可以通过向量范数| L | p来测量,该范数中定义p=1,2,…:

特殊情况|L|∞ 被定义为:

L2范数具有特殊的意义,被定义为:

L2范数代表了残差δu中所包含的剩余能量,在残差能量最小的情况下可以找到一个最优模型。因此,最优模型是一个非线性优化问题的解。
3.2 How to find an optimum model
图3.2显示了作为两个模型参数λ和μ函数的空间中一个点的剩余能量的化学示意图。这些颜色代表剩余能量的不同值。红色区域代表高剩余能量的模型,而蓝色区域代表低剩余能量的模型。目的是找出红色十字记号标记的剩余能量的最小值。从参数空间的点m1=(λ1(x),μ1(x),ρ1(x),)开始,我们希望通过沿搜索方向δm1,步长为μ1迭代更新材料参数来确定最小值,迭代方式为
![]()
 图3.2:空间中某一点的剩余能量与两个模型参数m1和m2的函数关系示意图。蓝点表示参数空间中的起点,而红十字记号表示目标函数的最小值
图3.2:空间中某一点的剩余能量与两个模型参数m1和m2的函数关系示意图。蓝点表示参数空间中的起点,而红十字记号表示目标函数的最小值
为了确定最佳搜索方向δm1,我们将泰勒级数中起点附近的剩余能量E(m1+δm1)
展开:![]()
设置公式3.5关于δm1的导数为零:
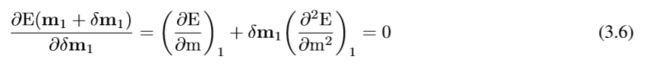
最终得出:
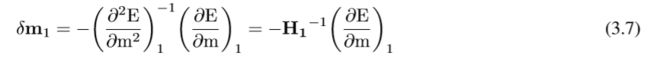
其中![]() 表示目标函数的最陡下降方向,
表示目标函数的最陡下降方向,![]() 表示逆Hessian矩阵。弹性问题的逆矩阵往往是唯一的,只能用高计算成本计算。因此,逆Hessian矩阵被一个预处理的算子P近似。对于一个优化预先设定的算子,没有一般规则。
表示逆Hessian矩阵。弹性问题的逆矩阵往往是唯一的,只能用高计算成本计算。因此,逆Hessian矩阵被一个预处理的算子P近似。对于一个优化预先设定的算子,没有一般规则。

用公式3.8代替公式3.4中的δm1,我们得到

最佳模型参数应位于能量的垂直梯度方向之前。起始点m1不是特定点,因此update函数可以应用于参数空间mn中的每个点

3.3 Calculation of the gradient direction
为了估计梯度方向∂E/∂m,剩余能量被重写为:
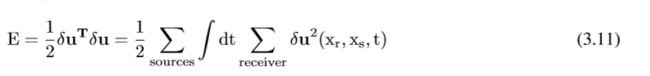
通过对模型参数m的推导,我们得到

公式(3.12)可与从数据到模型空间的微小变化映射相关,反之亦然(图3.3)。模型空间δm的微小变化,例如空间中某一点上的一个模型参数,将导致数据空间δu的扰动,例如地震剖面中的一个晃动

如果已知Frech’et导数∂u∂m,则模型空间中的所有小扰动可在模型体积V上积分,以计算数据空间中的总变化:

或者通过引入线性算子L:
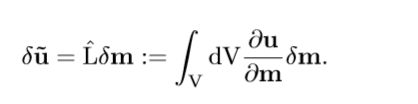
以类似的方式,数据空间的微小变化δu∮0可被积分以计算模型空间的总变化δm0
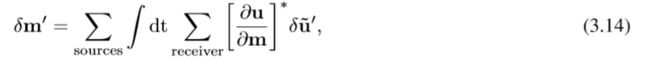
或作为算子方程
![]()
3.8 The elastic FWT algorithm
总的来说,FWT算法主要包含以下步骤:
1.在参数空间中定义模型m1。由于FWT码收敛速度慢、问题的非线性以及Born近似固有的计算梯度方向的特性,只能在主地震波长或以下重建结构,因此该模型应能很好地表示地下的长波长部分。
2.在迭代步骤n需要做:
(a) 对于每一个shot,解决正向问题,如公式(3.16)所述,实际模型mn生成合成数据集umod和波场u(x,t)。
(b) 计算地震数据x和y分量的剩余地震记录δu=umod-uobs。
(c) 通过反向传播接收位置的残差,生成波场Ψ(x,t)。
(d) 根据公式(3.35)计算各材料参数的梯度δmn。
(e) 为了提高收敛速度,在梯度δm

上应用了一个适当的预处理算子P。简单预处理算子的例子在第二章给出??
(f)为了进一步提高收敛速度,计算迭代步骤n≥2的共轭梯度方向:
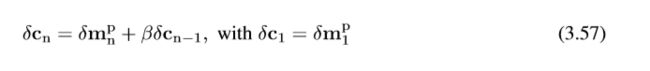
其中权重参数:

选择![]() 保证了polak-Ribi法的收敛性。
保证了polak-Ribi法的收敛性。
(g) 通过第3.6章中描述的线搜索算法估计步长μn。
(h) 使用梯度法更新材料参数:

如果材料参数不通过经验关系耦合,则必须同时更新所有三个弹性材料参数,否则强人工制品可能支配反演结果,特别是在非常复杂的介质情况下。
3.如果剩余能量E小于给定值,则停止迭代。否则继续下一个迭代步骤。
Chapter4 Source Time Function Inversion
导言:要将未知源时间函数(STF)的贡献从波形或设计中移除,需要设计一个滤波器,该滤波器对现场记录和合成图的影响最小。Thomas Forbriger的libraryLibSt文件是从TF软件导出的,可与IFOS2D中的C API一起使用。此库的目的是提供在全波形反演方法中推导源时间函数的方法。给定一组记录数据和一组合成数据(通常,但不一定是地下的脉冲响应),由于某种优化条件,得到源时间函数。用该小波对合成波形进行卷积,将卷积后的合成波形和小波本身返回给用户。
在这种情况下,源时间小波不一定是物理意义实验中所用源的实际力时程。源时间子波是指当合成波与该子波混合时,由于某些错误的条件,使合成波与记录波之间的错误最小化的子波。特别是这意味着合成波不一定是地下的脉冲响应(Greens函数),它们可能只是一些通用源子波(如Ricker子波)的合成波形计算。然后,导出的源时间函数必须相对于该一般小波来理解。
该库提供了不同的引擎来寻找最佳的源时间小波。操作的基本步骤是:
1.引擎已初始化。在这个步骤中,指向数组的指针连同一些头信息一起传递给引擎。发动机在记忆中的指定位置存储并期望记录数据以及合成。
2.调用engine的run()函数。engine记录和合成数据当前位于存储器阵列上,计算优化的小波,并通过将小波与卷积的合成小波一起复制到由发动机初始化器指示的存储器位置来返回小波。此步骤在每次计算合成数据后重复。
3.反演迭代结束后,移除engine
【如何构造参数字符串】
通过向库接口传递参数字符串来选择特定engine。此参数字符串还可以包含控制engine执行模式的参数。参数字符串以标识所需引擎的ID序列开始。在参数字符串中,ID序列以冒号(:)结尾。
选择所需的引擎后,接口函数将从参数字符串中除去ID序列和冒号,并初始化引擎,将引用传递给用户工作空间和参数字符串。参数字符串的其余部分可能由几个由冒号(:)分隔的控制参数组成。每个控制参数可能只是一个fliag(打开一个选项的开关),也可能带有一个参数值。参数值由等号(=)分隔。
举例:
•要选择频域最小二乘法并将返回的源时间函数移动0.4s并打开详细模式,请传递以下参数字符串:
![]()
•要选择频域最小二乘法,请应用与偏移量相关的权重,并使用2的幂来加速FFT:
![]()
【engine“傅里叶域最小二乘法(fdlsq)”的详细说明】
•dlk是频率fl处记录数据和偏移rk处接收器k的Fourier系数,
•slk是相应合成物的Fourier系数,
•ql是所寻求的源时间函数的Fourier系数,
那么这个engine将最小化目标函数关于的实部![]() 和虚部
和虚部![]() 的目标函数
的目标函数
![]()
![]()
在上述表达式中,
是带权重的数据错误,
用于正则化,并将在反褶积中引入水位。λ将平衡这两种贡献。条件式
导致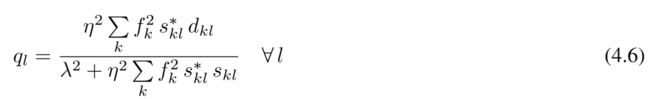
其中
fk是一个特定于接收机的加权因子。现在必须使用η和λ来平衡正则化。我们的目标是将水位指定为合成数据能量的一部分。
【设置水量】
如果残差dlk-slkql的标度能量等于合成slk的标度能量,则mis fit等于1,并且

是合成物标度能量的倒数。如果我们选择
其中N是频率的数目,那么![]() 将指定一个水位作为合成物的标度能量的分数。
将指定一个水位作为合成物的标度能量的分数。
【利用Parceval定理计算信号能量】
信号A(t)及其傅立叶变换α(ω)的PARCVEAR定理是![]()
如果Sjk是对应于Fourier系数的时间序列样本,而t是采样间隔,则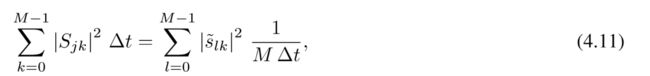
其中M=2N是时间序列中的样本数。在上述计算中,能量和仅使用正频率并且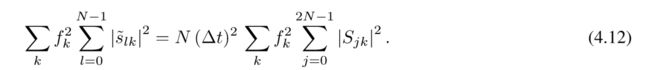
由st finv::STFFourierDomainEngine计算的Fourier系数slk不按比例缩放(参见libfourierxx和libfftw3的文档),因此
(slk和![]() 都是傅里叶系数)。因此
都是傅里叶系数)。因此
![]()
【最终计算配方】
我们的问题的最终解决法是:

当![]()
为接收器k的合成时间序列的平方样本值Sjk之和,fk为标度因子,![]() 为水位参数。
为水位参数。