几种常用回归算法——线性回归、支持向量机回归和KNN回归
台湾何时归——几种常用回归算法
- 线性回归LR(Linear Regression)
- 代码展示(加噪声的正旋函数,狭义线性回归)
- 支持向量机回归SVR(Support Vector Regression)
- 代码展示(加噪声的正旋函数,支持向量机回归)
- KNN回归(KNeighborsRegressor)
- 代码展示(加噪声的正旋函数,KNN回归)
- 对比总结:
线性回归LR(Linear Regression)
传统的多变量线性回归可以表示成下面的形式:——狭义的线性回归
f ( X , θ ) = X θ = θ 0 + x 1 θ 1 + x 2 θ 2 + … … + x n θ n (公式1) f(X, \theta) = X \theta = \theta_0 + x_1 \theta_1 + x_2 \theta_2 + …… + x_n \theta_n \tag{公式1} f(X,θ)=Xθ=θ0+x1θ1+x2θ2+……+xnθn(公式1)
这个模型的自变量是一次的,能解决的问题有很大的局限性,如果数据具有非线性的趋势,便不能得到很好的表达。将自变量扩展到高次的情况,便得到了多项式回归(拟合)。
f ( X , θ ) = X θ = θ 0 + θ 1 x + θ 2 x 2 + … … + θ n x n = ϕ ( X ) θ (公式2) f(X, \theta) = X \theta = \theta_0 + \theta_1 x + \theta_2 x^2 + …… + \theta_n x^n = \phi (X) \theta \tag{公式2} f(X,θ)=Xθ=θ0+θ1x+θ2x2+……+θnxn=ϕ(X)θ(公式2)
其中 ϕ ( X ) = [ 1 , x , x 2 , … … , x n ] , θ = [ θ 0 , θ 1 , θ 2 , … … , θ n ] T \phi(X) = [1, x, x^2, ……, x^n], \theta = [\theta_0, \theta_1, \theta_2, ……, \theta_n]^T ϕ(X)=[1,x,x2,……,xn],θ=[θ0,θ1,θ2,……,θn]T,将 ϕ ( X ) \phi (X) ϕ(X)称为基函数,这里我们选用了多项式基函数。选用不同的基函数能解决更为广泛的问题。——广义的线性回归
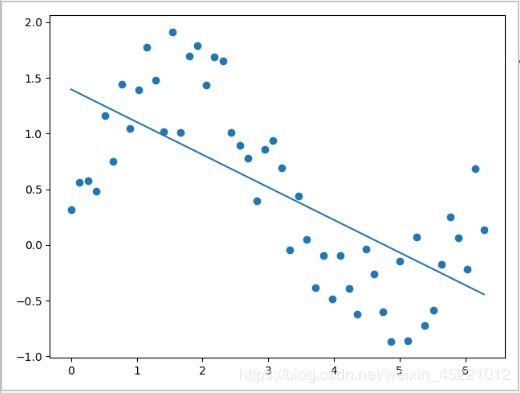
代码展示(加噪声的正旋函数,狭义线性回归)
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
import numpy as np
X = np.linspace(0, 2 * np.pi, 50)
y = np.sin(X) + np.random.random(size=(50,))
lr = LinearRegression()
lr.fit(X.reshape(-1, 1), y)
y_pred_lr = lr.predict(X.reshape(-1, 1))
plt.scatter(X, y)
plt.plot(X, y_pred_lr)
plt.show()
支持向量机回归SVR(Support Vector Regression)
返回顶部
支持向量机里面有核函数的概念,把数据映射到高维空间,隐式地应用了多项式,支持向量机回归能很好拟合非线性趋势。
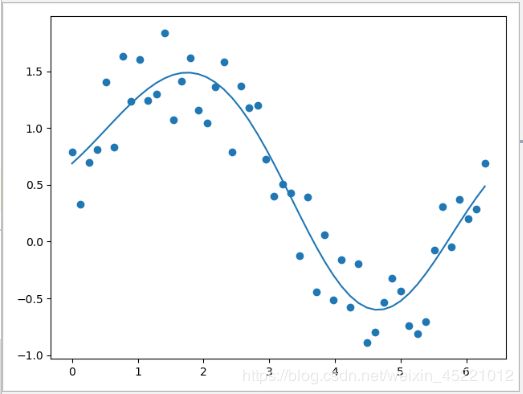
代码展示(加噪声的正旋函数,支持向量机回归)
from sklearn.svm import SVR
import matplotlib.pyplot as plt
import numpy as np
X = np.linspace(0, 2 * np.pi, 50)
y = np.sin(X) + np.random.random(size=(50,))
svr = SVR()
svr.fit(X.reshape(-1, 1), y)
y_pred_svr = svr.predict(X.reshape(-1, 1))
plt.scatter(X, y)
plt.plot(X, y_pred_svr)
plt.show()
KNN回归(KNeighborsRegressor)
返回顶部
非参数方法。
周围数据的平均值,默认用minkowski距离来选择最近的点。邻居数(n-neighbors)越大,越平滑(bias);越小,越过拟合(vias)
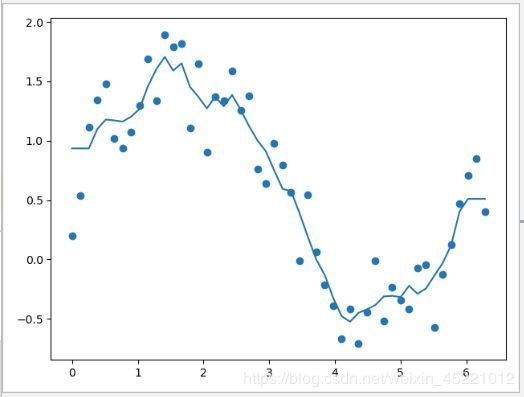
代码展示(加噪声的正旋函数,KNN回归)
from sklearn.neighbors import KNeighborsRegressor
import matplotlib.pyplot as plt
import numpy as np
X = np.linspace(0, 2 * np.pi, 50)
y = np.sin(X) + np.random.random(size=(50,))
knnr = KNeighborsRegressor()
knnr.fit(X.reshape(-1, 1), y)
y_pred_knnr = knnr.predict(X.reshape(-1, 1))
plt.scatter(X, y)
plt.plot(X, y_pred_knnr)
plt.show()
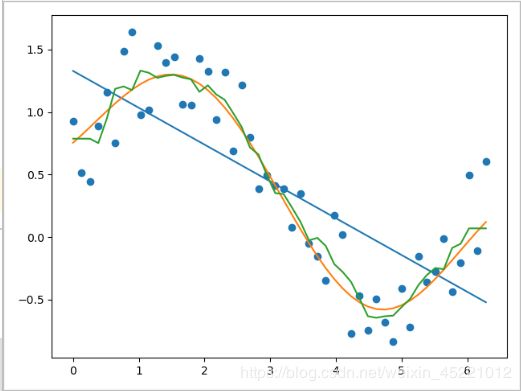
对比总结:
1. 狭义的线性回归不拟合非线性;
2. 支持向量机回归很好拟合非线性;
3. KNN可以拟合非线性(但不够平滑)。
写代码不忘国事!
欢迎关注,敬请点赞!
返回顶部