2020牛客暑期多校训练营（第二场）

B-Boundary

题意：二维平面上有 $n$ 个点，需要找到一个经过原点$(0,0)$的圆（半径自定），使得这个圆的圆弧经过尽可能多的那 $n$ 个点中的点，并且输出最大经过点的个数。

思路：三个点可以确定一个圆，算上必须经过的原点，我们就还需要再在这n个点中找两个出来，然后确定他们的圆心，这样枚举出所有可以构成的圆心(因为有可能不能构成，就是三点共线的时候)，选出最多的那一个就是最多点经过的圆的圆心了，现在只需要求出来是多少个点经过的它，构成的这么多圆心，我们就可以从 1～n 枚举 i ，计算 $C_i^2$ 代表在找有多少组两个的点可以构成圆心，当这个值等于统计出来的圆心最大值的时候，i 就是可以构成的最大点的数量。

#include 
using namespace std;

int n;
struct Point {
	double x, y;
} a[2005];
vector<pair<double, double> > mp, num;

pair<double, double> solve(Point a, Point b, Point c) {
	double X, Y;
	double fm1=2 * (a.y - c.y) * (a.x - b.x) - 2 * (a.y - b.y) * (a.x - c.x);
	double fm2=2 * (a.y - b.y) * (a.x - c.x) - 2 * (a.y - c.y) * (a.x - b.x);
 
	if (fm1 == 0 || fm2 == 0) {
		X = Y = 1e18;
		return make_pair(X, Y);
	}
	double fz1=a.x * a.x - b.x * b.x + a.y * a.y - b.y * b.y;
	double fz2=a.x * a.x - c.x * c.x + a.y * a.y - c.y * c.y;
	X = (fz1 * (a.y - c.y) - fz2 * (a.y - b.y)) / fm1;
	Y = (fz1 * (a.x - c.x) - fz2 * (a.x - b.x)) / fm2;
	return make_pair(X, Y);
}

int main() {
	scanf("%d", &n);
	for(int i = 1;i <= n; i++) {
		scanf("%lf %lf", &a[i].x, &a[i].y);
	}
	
	pair <double, double> cir;
	Point sour; sour.x = 0; sour.y = 0;
	for(int i = 1;i <= n; i++) {
		for(int j = i+1;j <= n; j++) {
			cir = solve(sour, a[i], a[j]);
			if(cir.first == 1e18 && cir.second == 1e18) continue;
//			printf("%lf %lf\n", cir.first, cir.second);
			mp.push_back(cir);
		}
	}
	if(mp.empty()) {puts("1"); return 0;} 
	sort(mp.begin(), mp.end());
	num.push_back(mp[0]);
	int ans = 1;
	for(int i = 1;i < mp.size(); i++) {
		if(mp[i] != num[0]) num.clear();
		num.push_back(mp[i]);
		ans = max(ans, (int)num.size());
	}
	
	for(int i = 1;i <= n; i++) {
		if(i*(i-1) == ans*2) {
			printf("%d\n", i);
			return 0;
		}
	}
}

C Cover the Tree

题意：给你一棵n和节点的树，然后给出组成这棵树的n-1条边。让你找最少的链，使得所有的链走过的节点覆盖了整棵树。答案需要你输出方案数和具体的方案。

思路：最优的想法就是从这个叶子结点连到另一个叶子结点，因为这样可以经过的节点最多。那么怎么去分配这些点呢，问题就在这里，解决了这个就没得问题了。

我们可以找一棵树随便玩一下：

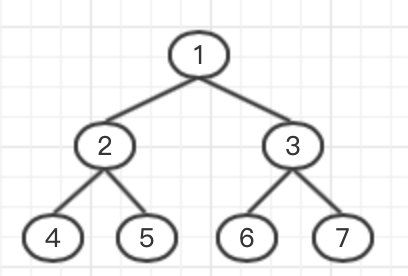
假如我们选择相邻的两个叶子结点，4和5 还有 6和7，那么我们是不是就无法覆盖到1节点，然后还需要再连接一条 4或者5 到 6或者7 的边才可以覆盖到1，那么我们可以想，前两条边就不能把连接1的事情顺便也给做了吗？ 然后再琢磨一下，是不是应该就可以想到让每个叶子结点找另一个叶子结点的时候都经过根节点，这样的话就可以让覆盖点的效率增加到最大了。并且也就是最少的链。

那么怎么找点才可以每次都经过根节点呢，我们可以先说一下这个链的数量最少就是叶子结点数量的一半，奇数情况就向上取整。 这样我们就可以理解为把所有的叶子结点分成两部分，左边和右边，按照dfs序分。假设mid为节点一半的数量，取到第i个点的时候，就找 i+mid 这个点连边，如果 i+mid 大于叶子结点个数而 i 还没有取完，证明这个是奇数情况的最后一个节点，就剩这个i没有找到边了，这个时候随便谁跟他配一下就好了。大概就是这样。

#include 
using namespace std;

int n;
vector <int> g[200005], leap;

void dfs(int pos, int fa) {
	if(g[pos].size() == 1) {leap.push_back(pos); return;}
	for(int i = 0;i < g[pos].size(); i++) {
		if(g[pos][i] == fa) continue;
		dfs(g[pos][i], pos);
	}
}

int main() {
	scanf("%d", &n);
	int u, v, head = 0;
	for(int i = 1;i < n; i++) {
		scanf("%d %d", &u, &v);
		if(!head) head = u;
		g[u].push_back(v);
		g[v].push_back(u);
	}
	
	for(int i = 1;i <= n; i++) {
		if(g[i].size() > 1) {head = i; break;}
	}
	
	dfs(head, -1);
	int mid = ((int)leap.size()+1)/2;
	printf("%d\n", mid);
	
	for(int i = 0;i < mid; i++) {
		if(i+mid >= (int)leap.size()) printf("%d %d\n", leap[i], leap[mid]);
		else printf("%d %d\n", leap[i], leap[i+mid]);
	}
}

/*
5
1 2
2 3
3 4
3 5
*/

D-Duration

题意：给两个同一天的时间的字符串，计算着两个时间相差多少秒

思路：把两个时间字符串处理成两个整型数作差即可

#include 
using namespace std;

string a, b;

int gettime(string s) {
	int h = 0, m = 0, ss = 0;
	for(int i = 0;i <= 1; i++) {
		h *= 10; h += s[i]-'0'; 
	}
	for(int i = 3;i <= 4; i++) {
		m *= 10; m += s[i]-'0'; 
	}
	for(int i = 6;i <= 7; i++) {
		ss *= 10; ss += s[i];
	}
	return ss+m*60+h*3600;
}

int main() {
	cin >> a >> b;
	int t1 = gettime(a);
	int t2 = gettime(b);
	if(t1 > t2) swap(t1, t2);
	printf("%d\n", t2-t1);
}

F - Fake Maxpooling

题意：给你一个 $n\ast m$ 的矩阵，每个节点的值就是它本身所在位置 $(i,j)$ 的最小公倍数 $lcm(i,j)$ 。求这个矩阵中大小为 $k\ast k$ 的所有子矩阵中最大值的和。

思路：子矩阵从左上角开始，向右或者向下平移一格就可以得到一个新的子矩阵。那么就可以分别维护在长度为的k区间中行的最大值和列的最大值。这样就可以维护出每个 $(i-k+1,j-k+1)->(i,j)$ 的矩阵的最大值了，维护最大值用双端队列模拟单调队列来做，如果当前的值大于队列中的front,那么就清空队列，否则就从尾部加入队列，这样当前位置就取front的值，也就是在长度为k的区间中的最大值，行和列分别维护一遍就可以了

#include 
using namespace std;

int n, m, k, a[5005][5005], maxn[5005][5005];
int gcd(int a, int b) {return b==0?a:gcd(b,a%b);}
int lcm(int a, int b) {return a*b/gcd(a,b);}

deque <int> q;

int main() {
	scanf("%d %d %d", &n, &m, &k);
	for(int i = 1;i <= n; i++) {
		for(int j = 1;j <= m; j++) {
			a[i][j] = lcm(i, j);
		}
	}
	
	for(int i = 1;i <= n; i++) {
		q.clear();
		for(int j = 1;j <= m; j++) {
			while(!q.empty() && a[i][q.front()] < a[i][j]) q.pop_back();
			q.push_back(j);
			while(q.front() <= j-k) q.pop_front();
			maxn[i][j] = a[i][q.front()];
		}
	}
	
	for(int j = 1;j <= m; j++) {
		q.clear();
		for(int i = 1;i <= n; i++) {
			while(!q.empty() && maxn[q.front()][j] < maxn[i][j]) q.pop_back();
			q.push_back(i);
			while(q.front() <= i-k) q.pop_front();
			a[i][j] = maxn[q.front()][j];
		}
	}
	
	long long ans = 0;
	for(int i = k;i <= n; i++) {
		for(int j = k;j <= m; j++) {
			ans += a[i][j];
		}
	}
	printf("%lld\n", ans);
}

G-Greater and Greater

题意：给一个长度为n的数组a，一个长度为m的数组b，需要在a中找到长度为m的区间s，使得这个s中的每一个元素都 ≥ 对应的b的元素，求这样的区间的个数。

思路：参考博客 这个题看题解之前也只有 $O(n\ast m)$ 的想法，这个复杂度必死无疑啊。看了之后发现优化了32倍，但是计算机一秒不是运行 $1e8$ 次吗，唉，时代变了。

这个题就是用bitset来优化常数，其实跟暴力是差不多的思路。拿样例来看一下

a : 1 4 2 8 5 7
b : 2 3 3

我们定义一个bitset $bs[i][j]$ ，当 $a[j]\ge b[i]$ 的时候 $bs[i][j]$ 为 1，否则为0。

那么样例中会产生三个bs

1 1 1 1 1 0
1 1 1 0 1 0
1 1 1 0 1 0

我们从题面的提示中或者根据得到的这三个bs式子看出，可以形成答案的在这三个bs形成的矩阵中 像这样斜着看" / " 所有的数字都是1，所以根据他们所在的行数i-1，向右 >> 移动i-1位，这样所有的答案是不是就可以对齐了？本来答案分布是这样的：

根据所在行号向右移动之后答案分布就像这样了：

为什么要有这一步的操作呢，就是好操作比较而已。那么我们如何去寻找biteset才可以避免 $O(n\ast m)$ 的复杂度呢？ 可以将a、b都进行从小到大排序，然后从尾部开始遍历，那么我们遍历的b数组中的数肯定是越来越小的，就比如样例这个 2 3 3，我们先拿3来跟a数组的每一个数比较，当遍历到a中有比3小的数时结束对于3的遍历，那么针对于这个位置的bitset就可以找到了，再遍历下一个数3的时候我们就不需要再次从a的尾部开始遍历，因为b按生序排列，比b后面的数打的数不可能比b前面的数要小，从上次中断的位置继续就可以了。得到的bitset就是对应b位置的大小关系，用上面讲到的右移的方法对一个ans & 操作，可以发现是答案的位置所有的数&过后仍然为1，否则为0，最后输出ans.count() 就可以了。

#include 
using namespace std;
const int maxn = 200005;
int n, m, x;
vector<pair<int, int> > a, b;
bitset <maxn> bs, ans;

int main() {
	scanf("%d %d", &n, &m);
	for(int i = 0;i < n; i++) {
		scanf("%d", &x);
		a.push_back(make_pair(x, i));
	} 
	for(int i = 0;i < m; i++) {
		scanf("%d", &x);
		b.push_back(make_pair(x, i));
	}
	
	sort(a.begin(), a.end());
	sort(b.begin(), b.end());
	ans.set();
	for(int j = m-1,i = n-1; j >= 0; j--) {
		while(i >= 0 && a[i].first >= b[j].first) {
			bs.set(a[i].second);
			i--;
		}
		ans &= (bs >> b[j].second);
	}
	printf("%d\n", (int)ans.count());
}

J - Just Shuffle

题意：给一个长度为 $n$ 的排列，和一个变换次数 $k$ ，给出正序排列变化 $k$ 次后的排列，让你根据一个变换规则求出变换一次后的排列是什么样子的。

思路：参考博客 .这个题意理解了很久，我觉得我这个讲的也不是很清晰，就拿样例来过一遍吧。

一个长度为3的排列 1 2 3 根据某种变换规则变换了998244353次以后成了 2 3 1，然后让我们根据这个变换规则求1 2 3变换一次的排列是什么样的。这样题意就很清晰了。我们根据样例的输出可以知道经过一次变化之后的样子来入手。可以发现这个例子的规则是这样的 3占了1的位置；1占了2的位置；2占了3的位置。这样就构成了一个环，在题目中一个排列可能会产生多个这样闭合的环 ，环与环之间互不干扰，各变各的。

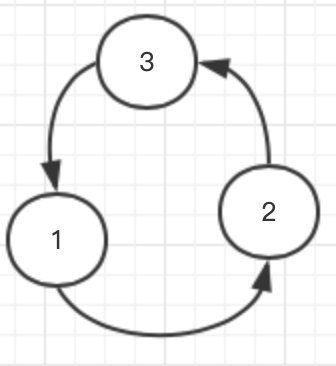
所以知道变化规则就可以求出答案了吗？是的，但是应该做不到。我们可以知道的这个数组中每几个数就会产生一个闭环，然后周期性的变换位置，就像 1 2 3 4 -> 3 4 1 2 可以有四种变换方式变成，使用一次的方法跟样例相似，两种的方法就是把整个排列向右移动，最后的放到最前面去，这个方法使用两次也可以变成这样，3、4次的方法就是1、2次的相反方向这个不是重点就不展开讲了，意思就是我们不能去猜或者去枚举排列的变换规则，这样的话复杂度会起飞的。

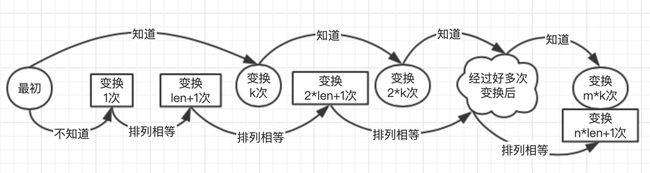
那么现在再来理一下思路，我们现在手里有什么条件？我们知道初始排列的状态，还知道变换k次后的排列，但是我们需要求的是初始状态变换一次后的样子。 我画个图来帮助理解一下：

那么请想一下，假如这个排列中的某一个环的循环节为len，那么这个环变化 $1$ 次和变换 $len+1$ 次是不是一样的，用样例来看 1 2 3 变换1次：3 1 2 ；变换2次：2 3 1；变换3次：1 2 3；变换4次：3 1 2； 那么变换 $2\ast len+1$ 次也是一样的，那么变换 $n\ast len+1$ 次想都不要想绝对还是一样的，好的这个问题先讨论到这里，再来看一下排列变换k次我们是知道长什么样的，那么变换 $2\ast k$ 次我们能不能知道呢？我们当然可以从初始状态直接推出到k状态是怎么变的，因为初始状态和k状态都有，位置变换规则就清楚，所以按照这个规则我们同样可以得到 $2\ast k$ 的序列吧，同理不假思索的就可以得到了 $m\ast k$ 次变换的排列具体是什么。我再来更新一下我们知道的信息的表示图：

再经过若干次变换之后在会有一种情况使得m次变换k次的排列与变换了$n\ast len+1$ 的排列完全相等，这个时候我们求出m等于多少是不是就可以得到最终的答案了

$m\ast k=n\ast len+1$ $->$ $m\%len\ast k\%len=1$

$m\%len$ 的范围也就是 $[0,len)$ ，枚举答案即可

得到了m就可以在这个数所在的环中查找答案了，假如就是样例的那个图，1变换两次会变成3，变换一次就成了2。公式就是这样的： $ans[v[i]]=v[(i+x)\%len]$ v[i] 是环中的数 这里的x就是m。应该不难理解的。

#include 
using namespace std;

int n, k;
int a[100005], ans[100005];
bool vis[100005];
vector <int> v;

void dfs(int pos) {
	if(vis[pos]) return;
	vis[pos] = 1;
	v.push_back(a[pos]);
	dfs(a[pos]);
}

void nice() {
	int len = v.size(), x;
	for(int i = 0;i < len; i++) {
		if(((long long)i*(k%len))%len == 1) {
			x = i; break;
		}
	}
	
	for(int i = 0;i < v.size(); i++) {
		ans[v[i]] = v[(i+x)%len];
	}
}

int main() {
	scanf("%d %d", &n, &k);
	for(int i = 1;i <= n; i++) {
		scanf("%d", &a[i]);
	}
	
	for(int i = 1;i <= n; i++) {
		if(!vis[i]) {
			v.clear();
			dfs(i);
//			for(int i = 0;i < v.size(); i++) printf("%d ", v[i]); puts("");
			nice();
		}
	}
	
	for(int i = 1;i <= n; i++) printf("%d ", ans[i]); puts("");
}