【论文笔记01】Learning Loss for Active Learning, CVPR 2019
目录导引
- 写在前面
- Learning Loss for Active Learning
- 1 Abstract
- 2 Contributions
- 3 Method
- 3.1 Overview
- 3.2 Loss Prediction Module
- 3.3 Learning Loss
- 4 Evaluation
- 4.1 Image Classification
- 4.2 Object Detection
- 4.3 Human Pose Estimation
- 参考文献
写在前面
大家好,这是我第一次在csdn上记录自己阅读论文的分享,内容有部分是自己做的转述,有的部分是自己的心得,希望对大家有帮助。也是作为自己的笔记。
Learning Loss for Active Learning
原文传送《Learning Loss for Active Learning》
本期分享是2019年发布在CVPR上的主动学习领域文章,《用学习损失来进行主动学习》,作者为来自韩国的Donggeun Yoo and In So Kewon.
论文引用和PDF地址在文末。
作者提出了一种通过预测模型预测误差来进行主动学习查询的方法,并用
- Image Classification(图像分类)
- Object Detection(目标检测)
- Human Pose Estimation(人体姿态估计)
三种任务进行性能评估。
1 Abstract
深度神经网络的表现随着更多有标注的数据而得到提升。但问题随之而来,我们能够用于标注的预算往往有限,这样的有标注数据不能无限获得。一种解决这种困难的方法是进行主动学习,让模型向人类询问,给部分数据打上标签。近年来学者提出很多的方法使得主动学习可以应用到深度网络上,但是他们中大多数是为了特定的目标任务设定,或者在计算上缺乏效率。
这篇文章提出一种创新的主动学习方法,简单而且任务无偏(task-agnostic)的,也在对深度网络上很有效率。作者给目标网络(Target Network)附带了一个参数量很小的模块,“误差预测模块”,用于预测模型对无标签数据预测结果的损失值。接下来,这个模块可以找到那些倾向于被目标网络预测错误的无标签数据。这个方法是任务无偏的,因为这个思想只是学习一个单纯的损失,与具体目标没有关系。
作者在三类问题上和当前的网络结构进行对比实验,结果表示Learning Loss在这些问题上一致地超越了其他方法。
2 Contributions
- Proposing a simple but efficient active laerning method with the loss prediction module, which is directly applicable to any takss with recent deep networks.
- 借用损失预测模块提出了一个简单但是高效的主动学习方法,它可以直接应用到任何使用深度网络的任务上。
- Evaluating the proposed method with three learning tasks including classification, regression, and a hybrid of them, by using current network architectures.
- 文章使用了三个学习任务对新方法进行测评,包括回归问题,分类问题以及回归和分类问题的混合。
3 Method
3.1 Overview
在这里,作者给出包含损失预测模块的主动学习方案的正式定义。
| Notation | Explanation |
|---|---|
| Θ t a r g e t {\Theta _{target}} Θtarget | target model 目标模型 |
| Θ l o s s {\Theta _{loss}} Θloss | loss prediction module 损失预测模块 |
| y ^ = Θ t arg e t ( x ) \hat y = {\Theta _{t\arg et}}(x) y^=Θtarget(x) | 目标模型的预测值 |
| l = L t a r g e t ( y ^ , y ) l = L_{target}(\hat y, y) l=Ltarget(y^,y) | 目标模型预测的损失 |
| h h h | x x x的特征集合,是 Θ t a r g e t {\Theta _{target}} Θtarget隐藏层的中间特征 |
| l ^ = Θ l o s s ( h ) \hat l = {\Theta _{loss}}(h) l^=Θloss(h) | 损失预测模块对损失的预测值 |
| U N U_N UN | 无标签数据池 |
| N N N | 无标签数据池的大小 |
| K K K | 每一轮从无标签数据池中查询的个数 |
| L K 0 L_K^0 LK0 | 初始有标签数据,即从 U N U_N UN均匀地抽 K K K个 |
| U N − K 0 U_{N-K}^0 UN−K0 | 初始化后的无标签数据池 |
| L ( T + 1 ) K T L_{(T+1)K}^T L(T+1)KT | T T T轮查询后的有标签数据集 |
| U N − ( T + 1 ) K T U_{N-(T+1)K}^T UN−(T+1)KT | T T T轮查询后的无标签数据池 |
图(1)摘自原文,其中
-
(a)展示的是从输入数据Input到目标网络给出的Traget prediction和利用网络中间特征传入误差预测模块而给出的Loss prediction部分。
-
(b)图表示的是通过Loss prediction的大小关系,挑选出 U N − ( T ) K ( T − 1 ) U_{N-(T)K}^{(T-1)} UN−(T)K(T−1)误差预测最大的 K K K个无标签数据点,送给专家进行标注后归入 L ( T ) K ( T − 1 ) L_{(T)K}^{(T-1)} L(T)K(T−1)更新得到有标签数据集 L ( T + 1 ) K T L_{(T+1)K}^T L(T+1)KT和无标签数据集 U N − ( T + 1 ) K T U_{N-(T+1)K}^T UN−(T+1)KT
-
补充说明一点,训练整个模型用的是有标签数据,无标签数据是在训练更新参数之后传入模型输出预测的损失,按照大小被选择部分进行查询。
3.2 Loss Prediction Module
损失预测模块是作者的任务无偏主动学习方法的核心,因为他可以仿照着学习不同具体任务下模型的损失,接下来阐述该文章如何具体做到这点。
损失预测模块致力于将为了主动学习设计具体任务相关的不确定性规则的工程量最小化。进一步,作者还希望把训练损失预测模块的计算代价最小化。为此,他们设计的损失预测模块有两个特点:
- 比任务模型(target model)小很多。
- 和任务模型同步学习(jointly),不需要额外的步骤。
图(2)摘自原文,具体阐释了损失预测模块的构成。
Target prediction的网络在图像上部,作者将深度网络分为若干中间块(Mid-block),依次提取出这些层的特征作为输入,传递到下方的小网络当中,最后汇聚到一个全连接层(Fully Connected Layer)得到损失预测值。
在每一个中间层特征传入的小网络中,包括一个全局平均池化层(Global Average Pooling),一个全连接层以及通过ReLU激活。通过在把所有中间特征汇聚到全连接层前的这些处理,作者将中间特征降维到固定的维度(128)。
另外,作者表示如果把这个损失预测模块做的更深更广,表现变化不大。
3.3 Learning Loss
本节描述学习损失预测模块的细节。
根据前面的定义和符号,在第 T T T步主动学习阶段,我们有有标签数据集 L ( T + 1 ) K T L_{(T+1)K}^T L(T+1)KT 和无标签数据集 U N − ( T + 1 ) K T U_{N-(T+1)K}^T UN−(T+1)KT,我们在这个一步的训练的目标是为模型集训练出 { Θ t a r g e t T , Θ l o s s T } \{\Theta_{target}^T,\Theta_{loss}^T\} {ΘtargetT,ΘlossT}。
根据任何一个训练数据 x , x ∈ L ( T + 1 ) K T x,x\in L_{(T+1)K}^T x,x∈L(T+1)KT,我们可以得到目标模型的预测值 y ^ \hat y y^,通过损失预测模块得到损失的预测值 l ^ \hat l l^,并且结合其真实标签 y y y 计算出它的真实损失 l = L t a r g e t ( y ^ , y ) l=L_{target}(\hat y, y) l=Ltarget(y^,y)。 l l l 作为 l ^ \hat l l^ 的真实值,又可以计算他们的损失 L l o s s ( l ^ , l ) L_{loss}(\hat l,l) Lloss(l^,l)。 结合这两部分损失就得到整体模型的损失。
L t a r g e t ( y ^ , y ) + λ L l o s s ( l ^ , l ) (1) L_{target}(\hat y, y) + \lambda L_{loss}(\hat l,l) \tag{1} Ltarget(y^,y)+λLloss(l^,l)(1)
图(3)摘自原文,补充描绘了损失函数的计算过程。
这里引入一些新的符号
| Notation | Explanation |
|---|---|
| L L L | 具体任务采用的损失函数,比如说MSE L l o s s ( l ^ , l ) = ( l ^ − l ) 2 L_{loss}(\hat l, l)=(\hat l-l)^2 Lloss(l^,l)=(l^−l)2 |
| λ \lambda λ | 缩放常数,调整前后项大小关系 |
| B T B^T BT | m i n i b a t c h , B T ∈ L ( T + 1 ) K T mini batch, B^T\in L_{(T+1)K}^T minibatch,BT∈L(T+1)KT |
| B B B | b a t c h s i z e , e v e n batch size,even batchsize,even |
关于损失估计的损失函数 L l o s s L_{loss} Lloss 的选择,作者表示 MSE 是本框架中不适用的,究其原因,随着真实的 l l l 值在一次次训练中下降, L l o s s ( l ^ , l ) = ( l ^ − l ) 2 L_{loss}(\hat l, l)=(\hat l-l)^2 Lloss(l^,l)=(l^−l)2 的减小似乎不一定代表损失预测模块对于损失预测的能力越来越强。因为 l ^ \hat l l^只需要适应 l l l 的变化,不需要更加贴合这个真实值就可以在迭代中造成 MSE 下降的把戏。作者通过尝试也确实验证了使用 MSE 不能获得一个好的损失预测模块。
我举了一个例子
| l l l | l ^ \hat l l^ | M S E MSE MSE | 误差比例 |
|---|---|---|---|
| 100 | 101 | 1 | 1% |
| 50 | 50.5 | 0.25 | 1% |
| 1 | 0.8 | 0.04 | 20% |
| 0.5 | 0.6 | 0.01 | 20% |
我们肯定不会认为下面的预测更好吧,这会造成损失预测大小关系的错乱,对我们查询不利。
接下来作者提出了适用于本实验的损失函数要求,就是无视 l l l 的量纲大小变化。在此,作者给出的答案是用对比一对样本构造损失函数。
在一个batch B T B^T BT 中,我们可以得到 B / 2 B/2 B/2 个样本对 { x p = ( x i , x j ) } \{x^p=(x_i, x_j)\} {xp=(xi,xj)},作者通过考虑这一对数据预测的损失差异来度量损失函数值:
L l o s s ( l ^ p , l p ) = m a x ( 0 , − I ( l i , l j ) ∗ ( l ^ i − l ^ j ) + ξ ) (2) L_{loss}(\hat l^p, l^p)=max(0,-I_{(l_i,l_j)}*(\hat l_i - \hat l_j) + \xi) \tag{2} Lloss(l^p,lp)=max(0,−I(li,lj)∗(l^i−l^j)+ξ)(2)
I ( l i , l j ) = { + 1 , i f l i > l j − 1 , o t h e r w i s e (3) I_{(l_i,l_j)}=\begin{cases} +1,&if \ l_i>l_j \\ -1,&otherwise \end{cases} \tag{3} I(li,lj)={+1,−1,if li>ljotherwise(3)
其中 ξ \xi ξ 是一个预先设定的正间隔,下标 p p p 指的就是样本对 ( i , j ) (i,j) (i,j). 对于上述式子的理解,当 l i > l j l_i > l_j li>lj 的时候,只有 l ^ i \hat l_i l^i 大于 l ^ j + ξ \hat l_j + \xi l^j+ξ 的时候才有损失值=0。其他情况下损失值不为零,以期增大 l ^ i \hat l_i l^i 并且减小 l ^ j \hat l_j l^j。
| case | L l o s s L_{loss} Lloss | = 0 =0 =0 |
|---|---|---|
| l i > l j l_i > l_j li>lj | m a x ( 0 , l ^ j − l ^ i + ξ ) max(0, \hat l_j - \hat l_i + \xi) max(0,l^j−l^i+ξ) | l ^ i > l ^ j + ξ \hat l_i > \hat l_j + \xi l^i>l^j+ξ |
| l j > l i l_j > l_i lj>li | m a x ( 0 , l ^ i − l ^ j + ξ ) max(0, \hat l_i - \hat l_j + \xi) max(0,l^i−l^j+ξ) | l ^ j > l ^ i + ξ \hat l_j > \hat l_i + \xi l^j>l^i+ξ |
考虑T步的一个mini-batch B T B^T BT, 文章最终用于同步更新目标模型和损失预测模块的损失函数总结为如下形式:
1 B ∑ ( x , y ) ∈ B T L t a r g e t ( y ^ , y ) + λ 2 B ∑ ( x p , y p ) ∈ B T L l o s s ( l ^ p , l p ) (4) \frac{1}{B}\sum\limits_{(x,y) \in {B^T}} L_{target}(\hat y, y) + \lambda \frac{2}{B}\sum\limits_{(x^p,y^p) \in {B^T}} L_{loss}(\hat l^p, l^p) \tag{4} B1(x,y)∈BT∑Ltarget(y^,y)+λB2(xp,yp)∈BT∑Lloss(l^p,lp)(4)
将这个损失函数最小化可以同时让我们得到 { Θ t a r g e t T , Θ l o s s T } \{\Theta_{target}^T,\Theta_{loss}^T\} {ΘtargetT,ΘlossT}。因为 Θ l o s s T \Theta_{loss}^T ΘlossT 只有少量的参数,却用上了目标模型中间层丰富的特征 h h h 。 T 步训练得到参数之后,我们把无标签数据送进进行损失预测,挑选出 K K K 个损失值最大的,也就是信息量最大的数据点进行人工标注,用新的标签数据集 L ( T + 2 ) K T + 1 L_{(T+2)K}^{T+1} L(T+2)KT+1 开始下一轮的训练。
4 Evaluation
4.1 Image Classification
- 数据集: 使用CIFAR-10数据集,初始的无标记数据池用里头的50000条数据建构 U 50000 U_{50000} U50000
- 查询: 每一轮迭代中,只从 U U U 中随机选择子集 M 10000 M_{10000} M10000 进行损失评估和查询
- 深度网络: 作者使用稍作修改的ResNet-18作为深度网络框架。
- 损失预测模块:ResNet-18在第一个卷积层之后包含四个基本块(也就是Residual Block),每一个基本块包含相邻的两个卷积层,损失预测模块的输入特征就是从这四个block引出来的。
- 数据增强: 随即裁剪、随机反转、mean-std标准化等
- 参数设置: λ = 1 , ξ = 1 \lambda = 1, \xi = 1 λ=1,ξ=1
- 优化器,学习率,batch: 略
- 对比方法: random samplling, entropy-based sampling, core-set sampling
-
- core-set方法上,作者使用了K-Center-Greedy算法,《ACTIVE LEARNING FOR CONVOLUTIONAL NEURAL NETWORKS: A CORE-SET APPROACH》
对比结论:
- 作者提出的方法在分类问题上险胜core-set和entropy-based,最后一轮的精确度分别为0.9101,.9010和0.9059。
- Learn Loss方法的优势在于可以高效地应用到更加复杂多样的任务上。
作者还使用另外一种评价方法来侧亮损失预测模块地表现。对于一对数据,如果模型预测出来损失大小关系正确,给予1的分数,否则为0分,图(5)展示了这种评价标准下模型在测试集上的表现情况。
图中有四根折现,按照图里顺序从上至下分别代表:
- 用文中推荐的 L l o s s ( l ^ p , l p ) L_{loss}(\hat l^p, l^p) Lloss(l^p,lp) 进行训练的损失预测模块,在CIFAR-10上的表现
- 用 MSE 进行训练的损失预测模块, λ = 0.1 \lambda = 0.1 λ=0.1, 在CIFAR-10上的表现
- 目标检测任务(4.2),在PASCAL VOC 2007+2012 数据集上测试
- 人体姿态估计任务(4.3),在MPII数据集上测试
观察前两条曲线不难发现,随着查询图片的增长,Ranking accuracy明显上升后平缓,第一条线趋于0.9074,第二条线一直落后于他,同时也在图(4)中表现出这个差距。
笔者认为这说明两点问题
- 作者提倡的损失函数是更有效地,MSE不适用
- Ranking accuracy对模型能力的测量是靠谱的
4.2 Object Detection
目标检测问题需要
- 定位一个语义对象的边界框,
- 还要识别这个对象的类别。
所以需要结合回归以及分类问题。
- 数据集: VOC2007的trainval’07以及VOC2012的trainval’12作为最初的无标签数据池。共 5011 + 11540 = 16551 5011+11540=16551 5011+11540=16551 条数据。测试集为VOC2007中的test’07,共4952条数据。
- **随机子集:**由于训练集总量没有CIFAR10中的那么大,本节中作者不设置随机子集以缩小每次迭代的查询范围。
- 目标模型: SSD (Single Shot Multibox Detector)
- 损失预测模块: 从SSD中提取了六层特征用于损失估计。 c o n v i ∣ i = 4 3 , 7 , 8 2 , 9 2 , 1 0 2 , 1 1 2 {conv_i | i = 4_3, 7, 8_2, 9_2, 10_2, 11_2} convi∣i=43,7,82,92,102,112
- 参数设置: λ = 1 , ξ = 1 \lambda = 1, \xi = 1 λ=1,ξ=1
- 其他训练内容与细节: 略
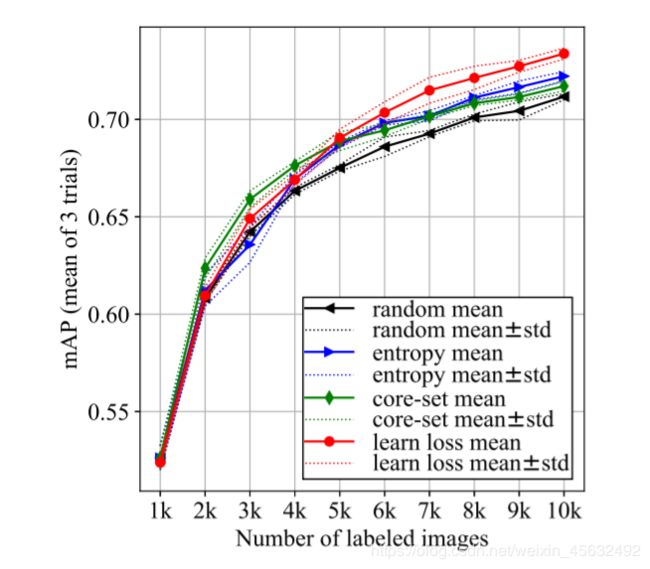
Figure6 Active learning results of object detection over PASCAL VOC 2007+2012
4.3 Human Pose Estimation
该任务的目的是从一张图像当中定位所有身体部位。监督学习需要每个身体部位的点标注。由于预测目标是一个点集,它常常被归为回归问题。
- 数据集: MPII dataset,其中训练集有22246个姿态,对应14679张图片;测试集有2958个姿态,对应2729张图片。无标签池记为 U 22246 U_{22246} U22246
- 随机子集: S 5000 S_{5000} S5000,每一轮我们随机抽取5000条数据,作为查询的备选。
- 评估方法: PCK(Percentage of Correct Key-points)
- 目标模型: Stacked Hourglass Networks
- 损失预测模块: 对于每一个hourglass network,身体部位热力图都是从最后一个特征图谱中得到的,作者继承两个hourglass network,分别提取他们的最后一层特征图谱,送到损失预测模块。

Figure7 Active learning results of human pose estimation over MPII
参考文献
[1]: Yoo, Donggeun, and In So Kweon. “Learning loss for active learning.” Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2019.
[2]: https://openaccess.thecvf.com/content_CVPR_2019/papers/Yoo_Learning_Loss_for_Active_Learning_CVPR_2019_paper.pdf




