Java 数据结构 -- 20.Java 8 数据结构补充介绍 ArrayDeque
前言
书接上文,上一篇对 EnumMap 进行了介绍与分析,本篇将对 ArrayDeque 进行介绍与分析。
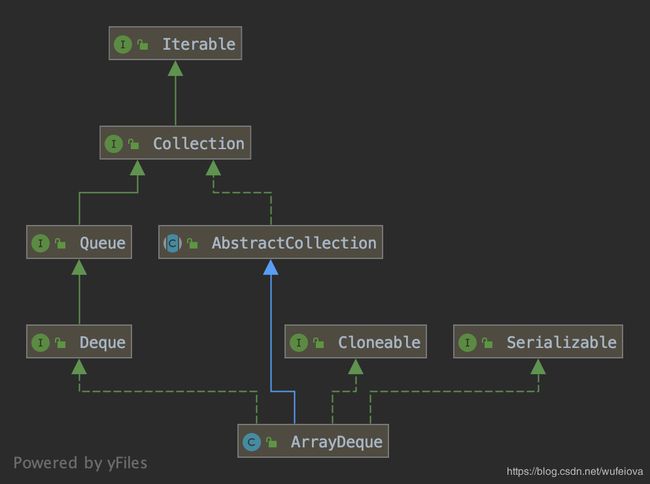
可以看到它与其他数据结构不同的地方主要是实现了双端队列(Deque 接口)。
由于 ArrayDeque 可以作为一个栈使用,所以在查看 ArrayDeque 之前先来看一下 Stack 的源码。
/**
* Stack 类代表了一个后进先出(LIFO)的对象s栈。它继承自 Vector 类的五个操作s允许一个 vector 被作为一个
* 栈使用。通常的 push 和 pop 操作s被提供,同样有一个方法来 peek 栈顶的元素,一个方法来测试是否栈是空的,
* 还有一个方法来查询栈中的一个元素并且发现它离栈顶有多远。
*
* 当一个栈第一次被创建时,它不包含任何元素s。
*
* 一个更完整与一致的 set 栈操作s被 {@link Deque} 和它的实现类s接口提供,它(Deque 和它的实现类)应该优
* 先于这个类使用。比如:
*
* {@code
* Deque stack = new ArrayDeque();}
*
* Stack 类继承自 Vector 的,Vector 可以认为是一个线程安全的 ArrayList,所以 Stack 中的大部分操作也是
* 线程安全的。Stack 中几乎所有的操作都是依赖于 Vector 调用的,所以 Stack 本身只是 Vector 适配栈特性适配
* 器。
*/
public
class Stack<E> extends Vector<E> {
/**
* 无参构造器,构造一个空的栈。
*
* 这里也就是说,栈虽然也是维护一个对象数组(从 Vector 继承来的维护特性),但是它并没为数组定义默认长
* 度,调用完 Stack 构造器后,会调用 Vector 无参构造器,将这个数组的长度置为 10(默认)
*/
public Stack() {
}
/**
* 想当前栈顶推一个元素。这与:
*
* addElement(item)
* 的影响是完全相同的。
*/
public E push(E item) {
addElement(item); //Vecor#addElement(synchonized)
return item; //返回参数
}
/**
* 移除当前栈最顶部的对象并且返回那个对象作为这个功能的值。
*/
public synchronized E pop() {
E obj;
int len = size(); //#size
obj = peek(); //#peek
removeElementAt(len - 1); //Vector#removeElementAt(synchronized)
return obj; //返回 obj
}
/**
* 查看当前栈顶的对象而不从这个栈中移除它。
*/
public synchronized E peek() {
int len = size(); //Vector#size(synchonized)
if (len == 0)
throw new EmptyStackException();
return elementAt(len - 1); //Vector#elementAt(synchronized)
}
/**
* 测试当前栈是不是空的。
*/
public boolean empty() {
return size() == 0; //Vector#size(synchonized)
}
/**
* 返回一个对象在当前栈中基于 1 的位置。如果对象 o 是当前栈的一个元素,这个方法返回距离栈顶到最近的这个
* 元素的引用,这个栈中离顶部最近的元素被认为是在距离 1 的。equals 方法被使用来比较 o 和当前栈中的元
* 素。
*/
public synchronized int search(Object o) {
int i = lastIndexOf(o); //Vector#lastIndexOf
if (i >= 0) { //说明存在
return size() - i;
}
return -1; //说明不存在
}
/** use serialVersionUID from JDK 1.0.2 for interoperability */
private static final long serialVersionUID = 1224463164541339165L;
}
从 Stack 的源码中可以看到,Stack 对于栈特性的实现主要是通过核心代码 elementAt(len - 1) 来完成的,它的核心是一个线程安全的数组链表容器(Vector)。
在查看 ArrayDeque 源码之前有一个概念需要解释:摊还时间
Amortised time explained in simple terms:
If you do an operation say a million times, you don’t really care about the worst-case or the best-case of that operation - what you care about is how much time is taken in total when you repeat the operation a million times.
So it doesn’t matter if the operation is very slow once in a while, as long as “once in a while” is rare enough for the slowness to be diluted away. Essentially amortised time means “average time taken per operation, if you do many operations”. Amortised time doesn’t have to be constant; you can have linear and logarithmic amortised time or whatever else.
Let’s take mats’ example of a dynamic array, to which you repeatedly add new items. Normally adding an item takes constant time (that is, O(1)). But each time the array is full, you allocate twice as much space, copy your data into the new region, and free the old space. Assuming allocates and frees run in constant time, this enlargement process takes O(n) time where n is the current size of the array.
So each time you enlarge, you take about twice as much time as the last enlarge. But you’ve also waited twice as long before doing it! The cost of each enlargement can thus be “spread out” among the insertions. This means that in the long term, the total time taken for adding m items to the array is O(m), and so the amortised time (i.e. time per insertion) is O(1). 摘自 stackoverflow
摊还时间可以理解为执行长时间相同(存在扩容等步移操作)操作后,平摊到每一次操作所要用时间。这里作者举了一个想 ArrayList 中添加一个元素的操作,当在达到扩容条件之前,加入一个元素的时间复杂度是 O(1),当将入一个元素正好需要扩容时,需要分配(这里只是打个比如)两杯空间,复制数据,然后将旧的空间释放。假设分配和释放需要恒定的时间,那么对于当前长度是 n 的 ArrayList,扩容步骤的时间复杂度就是 O(n)。所以每次扩容都需要前一次扩容的两杯时间,但是其实你已经在扩容它之前就已经等待了两倍的时间(这里的意思应该是对比上一次扩容时)!因此每次扩容的耗费在插入时就“飞走了”。这意味着在一个很长的时间内,插入 m 个元素s 的总时间复杂度是 O(m)(虽然平均每次所花费的时间随着扩容操作慢慢地被拉长了),这就是摊还时间。
对于性能的优劣可以理解为:
常数时间优于摊还时间,摊还时间优于线性时间
接着来了解一下 Java 对于双端数组队列的大致实现方式:
ArrayDeque 其实维护的是一个对象数组,并且可以以环绕的方式访问数组,但是数组本身是不具备这种特性的,Java 对其的实现方式是通过两个手段:
1、控制数组永远不被装满,并且 head 永远不等于 tail(除了数组为空的情况),其他情况在 head 将要等于 tail 的时候,都会自动进行双倍扩容
2、建立在第一条之上,通过位与“规化”操作来达到在操作数组的过程中不会出现越界的问题。
这里引用蓝灰_q 的《深入理解 ArrayDeque的设计与实现》文章 中的图例会看的更加清楚
先来看一张普通数组容器与双端数组容器在插入数据时的不同实现方式:

下图中上面那个是普通数组容器(比如 ArrayList)的插入方式,在 ArrayList 的源码中也可以看到其实是调用了 System#arraycopy 方法,这个 native 方法虽然高效但是还是会分配(或者不分配,单纯移动元素)新的数组;下面那个就是双端数组容器的插入方式,它是允许在物理上的第一个元素之前进行插入的,而这个元素的插入不会引起其他数据的大面积移动(只有在扩容和拷贝的时候才会调用 System.arraycopy 完整的复制数组,其他调用 System.arraycopy 的情况只有在 delete 时)。
再看一张图来了解一下双端数组容器的大致物理结构:

通过这张图可以看到,双端数组容器在逻辑上是连续的,但是在物理上并不一定,它的 head(语义头)并不总是在 tail(语义尾) 左边的,在塞入数据之前,head == tail,假设这个双端数组容器是以无参构造器构造的一个长度为 16 的容器,这是第 0 次扩容,head 与 tail 在对容器本身(与迭代器无关)进行操作的时候会被更新,这里需要注意的主要有两点:
1、某种操作在导致 head 或者 tail 超出了数组长度时该如何处理?
2、何时对数组进行扩容?
带着这两个问题,再来查看 ArrayDeque 的源码
/**
* {@link Deque} 接口的可变长度数组实现类。Array deques 没有容量限制;它们在需要时扩展来支持使用。它
* 们不是线程安全的,在没有(实现)外部同步的情况下,它们不支持通过多线程并发访问。null 元素s时被禁止的。
* 这个类在作为一个栈时看上去比 {@link Stack} 要更快,并且作为一个队列的时候比 {@link LinkedList}。
*
* 大部分 {@code ArrayDeque} 操作s在要给摊还常量时间内完成。除了 {@link #remove(Object)
* remove}, {@link #removeFirstOccurrence removeFirstOccurrence},{@link
* #removeLastOccurrence removeLastOccurrence},{@link #contains contains}, {@link
* #iterator iterator.remove()} 和扩展操作s例外,这些都在线性时间内完成。
*
* 这个类的 {@code iterator} 方法返回的迭代器s是 fail-fast 的:如果这个 deque 在迭代器创建后的任何
* 时间点被修改了,以任何除了通过迭代器自身的 {@code remove} 方法的方式,这个迭代器通常会抛出一个
* {@link ConcurrentModificationException}。因此,对于并发修改,迭代器失败的快速与干净,而不是在未
* 来某个不确定的时间点冒险做任何不确定的行为。
*
* 注意一个迭代器的 fail-fast 行为不能提供像它所描述的那样的保证,一般来说,不可能对于不同步的并发操作做
* 任何硬性的保证。基于最好性能的基础,fail-fast 迭代器抛出一个 ConcurrentModificationException。
* 因此,编写一个依赖于这个异常来保证其正确性的程序是错误的:迭代器的 fail-fast 行为应该只被用于检查
* bugs。
*
* ArrayDeque 类继承自 AbstractCollection 类,实现了 Deque 接口,Cloneable 接口,Serializable
* 接口
*/
public class ArrayDeque<E> extends AbstractCollection<E>
implements Deque<E>, Cloneable, Serializable
{
/**
* deque 存储的元素被放在数组中。这个 deque 的容量是这个数组的长度,它总是 2 的幂次方。这个数组永远
* 不允许放满,除非短暂地在一个 addx 方法它在快要满的时候被快速地重新分配大小(查看
* doubleCapacity),从而避免头和尾缠绕在一起,彼此相等。我们也保证所有不存储 deque 元素的数组元素
* s总是 null。
*/
transient Object[] elements; // 非私有的来简化内部类访问
/**
* 这个元素对于 deque 头部的位置(就是将被元素通过 remove() 或者 pop() 方法被移除的),或者如果这
* 个 deque 是空的话一个任意的与尾相等的(元素)。
*/
transient int head;
/**
* 下一个元素将被添加到这个 deque 尾部(通过 addLast(E),add(E),或者 push(E))的位置。
*/
transient int tail;
/**
* 我们将为一个新创建的 deque 使用的最小容量。必须是 2 的幂次方。
*/
private static final int MIN_INITIAL_CAPACITY = 8;
// ****** 数组分配操作和重新分配大小工具 ******
//计算长度
private static int calculateSize(int numElements) {
int initialCapacity = MIN_INITIAL_CAPACITY;
// 找到能够容纳元素s的最佳的 2 的幂次方的值
// 测试 “<=” 因此数组s不能保持满(不能等于)。
if (numElements >= initialCapacity) { //如果元素数量大于等于初始化容量
initialCapacity = numElements;
//找到适合大小
initialCapacity |= (initialCapacity >>> 1);
initialCapacity |= (initialCapacity >>> 2);
initialCapacity |= (initialCapacity >>> 4);
initialCapacity |= (initialCapacity >>> 8);
initialCapacity |= (initialCapacity >>> 16);
initialCapacity++;
if (initialCapacity < 0) // 太多元素s,必须后退(这里应该是越界导致小于 0)
initialCapacity >>>= 1;// 运气不错,分配到 2 ^ 30 个元素
}
return initialCapacity; //返回 initialCapacity
}
/**
* 分配空数组来保存指定数量的元素s。
*/
private void allocateElements(int numElements) {
elements = new Object[calculateSize(numElements)]; //#calculateSize
}
/**
* 成倍增长这个 deque 的容量。只有在满的时候调用,比如,当头与尾缠绕相等时。
*/
private void doubleCapacity() {
assert head == tail;
int p = head;
int n = elements.length;
int r = n - p; // p 右边的元素s数量
int newCapacity = n << 1; //乘以 2
if (newCapacity < 0)
throw new IllegalStateException("Sorry, deque too big"); //越界了
Object[] a = new Object[newCapacity];
//System#arraycopy(Object src, int srcPos, Object dest, int destPos, int length)
System.arraycopy(elements, p, a, 0, r); //调用底层复制数组方法,就像 ArrayList 那样,这里是原来 elements 元素的反向获取从 p 到 0,分配长度为 r
System.arraycopy(elements, 0, a, r, p); //这里是原来 elements 元素的正向获取从 0 到 r,分配长度为 p
elements = a; //启用新数组
//重置 head,tail(由于后面还没有元素)
head = 0;
tail = n;
}
/**
* 按顺序(从 deque 中的第一个到最后一个元素)从我们的元素数组中拷贝元素s到指定数组中。它被假设这个
* 数组是足够大来持有所有 deque 中的元素s的。
*/
private <T> T[] copyElements(T[] a) {
if (head < tail) { //如果 head 小于 tail
System.arraycopy(elements, head, a, 0, size()); //拷贝的是 head 到 0 的数据
} else if (head > tail) { //这里可以看到 head 是可能大于 tail
int headPortionLen = elements.length - head;
System.arraycopy(elements, head, a, 0, headPortionLen); //拷贝到是 head 到 0 的数据
System.arraycopy(elements, 0, a, headPortionLen, tail); //考别的是 0 到 headPortionLen 的数据
} //不用考虑相等的情况(#calculateSize 中已经避免了)
return a;
}
/**
* 使用一个足以容纳 16 个元素s的初始化容量构造一个 ArrayDeque。
*/
public ArrayDeque() {
elements = new Object[16]; //默认 16
}
/**
* 使用一个足以容纳指定元素s数量的初始化容量沟构造一个 ArrayDeque。
*/
public ArrayDeque(int numElements) {
allocateElements(numElements); //#allocateElements
}
/**
* 构造一个包含指定 collection 中所有元素的 deque,以这个 collecction 的迭代器返回元素的顺序。
* (第一个由 collection 的迭代器返回的元素成为(deque 的)第一个元素,或者 deque 的前部。)
*/
public ArrayDeque(Collection<? extends E> c) {
allocateElements(c.size()); //#allocateElements
addAll(c); //#addAll
}
// 主要的插入和提取方法s addFirst,addLast, pollFirst, pollLast。其他方法s是基于这些方法定义的。
/**
* 在当前 deque 的前部插入指定元素。
*/
public void addFirst(E e) {
if (e == null)
throw new NullPointerException();
/**
* 规化递增 head,对于位与第二个元素 elements.length - 1 我的猜想是由于 elements 永远不允
* 许放满,所以当 head 要么小于 elements.length,要么大于,大小于时,位与的结果就是 head -
* 1,也就是当前 head 的前一个位置,当大于时候,位与的结果就是 0,elements 从头开始
**/
elements[head = (head - 1) & (elements.length - 1)] = e;
if (head == tail) //缠绕判断
doubleCapacity(); //#doubleCapacity
}
/**
* 在当前 deque 的末尾添加指定元素。
* 这个方法和 {@link #add} 是相同的。
*/
public void addLast(E e) {
if (e == null)
throw new NullPointerException();
elements[tail] = e; //e 赋值给 elements 尾位置
/**
* 规化递减 tail,与更新 head 类似,小于 elements.length - 1 时就是自己 + 1,否则是 0,判
* 断是否缠绕
**/
if ( (tail = (tail + 1) & (elements.length - 1)) == head)
doubleCapacity(); //#doubleCapacity
}
/**
* 在当前 deque 的前部插入指定元素。
*/
public boolean offerFirst(E e) {
addFirst(e); //#addFirst
return true; //返回 true
}
/**
* 在当前 deque 的后部插入指定元素。
*/
public boolean offerLast(E e) {
addLast(e); //#addLast
return true; //返回 true
}
//移除第一个元素方法
public E removeFirst() {
E x = pollFirst(); //#pollFirst
if (x == null)
throw new NoSuchElementException();
return x; //返回 x
}
//移除最后一个元素方法
public E removeLast() {
E x = pollLast(); //#pollLast
if (x == null)
throw new NoSuchElementException();
return x; //返回 x
}
//获得并移除第一个元素方法
public E pollFirst() {
int h = head; //缓存 head
@SuppressWarnings("unchecked")
E result = (E) elements[h];
// 如果 deque 是空的,元素是 null
if (result == null)
return null;
elements[h] = null; // 必须空出插槽
head = (h + 1) & (elements.length - 1); //规化递增 head
return result; //返回 result
}
//获取并移除最后一个元素方法
public E pollLast() {
//这里可以看到,tail 位置应该是不存放元素的(也是为了避免与 head 缠绕)
int t = (tail - 1) & (elements.length - 1);
@SuppressWarnings("unchecked")
E result = (E) elements[t];
if (result == null)
return null;
elements[t] = null; //空槽操作
tail = t; //tail 更新为 t
return result; //返回 result
}
//获取第一个元素方法
public E getFirst() {
@SuppressWarnings("unchecked")
E result = (E) elements[head]; //直接获取 head 位置元素,不移动 head,不清空插槽
if (result == null)
throw new NoSuchElementException();
return result; //返回 result
}
//获取最后一个元素方法
public E getLast() {
@SuppressWarnings("unchecked")
E result = (E) elements[(tail - 1) & (elements.length - 1)]; //获取规化 tail - 1 位置元素,不移动 tail,不清空插槽
if (result == null)
throw new NoSuchElementException();
return result; //返回 result
}
//查看第一个元素方法
@SuppressWarnings("unchecked")
public E peekFirst() {
//直接获取 head 位置元素,不判断是否为 null
return (E) elements[head]; //如果 deque 是空的,那么结果就是 null
}
//查看最后一个元素方法
@SuppressWarnings("unchecked")
public E peekLast() {
//直接获取规化 tail - 1 位置元素,不判断是否为 null,为什么不直接获取 tail - 1,没有想明白。。
return (E) elements[(tail - 1) & (elements.length - 1)];
}
/**
* 移除当前 deque 中第一个与指定元素匹配的元素(从头向尾横穿这个 deque 的过程中)。如果 deque 不包
* 含这个元素,它是不会被修改的。更正式地说,移除第一个存在 {@code o.equals(e)} 关系的元素
* {@code e} (如果这样的元素存在)。
*
* 如果当前 deque 包含指定元素则返回 {@code true}(或者等价的,作为如果当前 deque 被修改了的调用
* 结果)。
*
* 移除第一个相同的元素方法
*/
public boolean removeFirstOccurrence(Object o) {
if (o == null)
return false;
int mask = elements.length - 1;
int i = head; //从 head 开始
Object x;
while ( (x = elements[i]) != null) { //循环如果 elements i 位置的元素不为 null
if (o.equals(x)) {
delete(i); //#delete
return true; //返回 true
}
i = (i + 1) & mask; //这里对参数取了别名,其实还是规化递增 head
}
return false; //返回 false
}
/**
* 移除当前 deque 中最后一个与指定元素相同的元素(从头到位横穿这个 deque)。如果这个 deque 不包含
* 这样的元素,它不被改变。
*
* 更一般地说,移除最后一个存在 {@code o.equals(e)} 关系的 {@code o.equals(e)} (如果存在一个
* 这样的元素的话)。
*
* 如果当前 deque 包含指定元素则返回 {@code true}(或者等价的,作为如果当前 deque 被修改了的调用
* 结果)。
*/
public boolean removeLastOccurrence(Object o) {
if (o == null)
return false;
int mask = elements.length - 1;
int i = (tail - 1) & mask; //这里为什么不直接使用 tail - 1,而要在规化一遍。。
Object x;
while ( (x = elements[i]) != null) {
if (o.equals(x)) {
delete(i);
return true;
}
i = (i - 1) & mask; //对参数取别名,规化递减 tail - 1
}
return false;
}
// *** 队列操作s ***
/**
* 向当前 deque 的最后插入一个指定元素。
*
* 这个方法等价于 {@link #addLast}。
*/
public boolean add(E e) {
addLast(e); //#addLast
return true; //返回 true
}
/**
* 向当前 deque 的最后插入一个指定元素。
*
* 这个方法等价于 {@link #offerLast}。
*/
public boolean offer(E e) {
return offerLast(e); //#offerLast
}
/**
* 获得并且移除代表当前 deque 的这个 queue 的头。
*
* 这个方法与 {@link #poll poll} 的区别只是如果当前 deque 是空的,那么它抛出一个异常。
*
* 这个方法等价于 {@link #removeFirst}。
*/
public E remove() {
return removeFirst(); //#removeFirst
}
/**
* 获取并且移除代表当前 deque 的这个 queue 的头()。(或句话说,当前 deque 的第一个元素),或者如果
* 当前 deque 为空则返回 {@code null}。
*
* 这个方法等价于 {@link #pollFirst}。
*/
public E poll() {
return pollFirst(); //#pollFirst
}
/**
* 返回,但是不移除,代表当前 deque 的 queue 的头。这个方法与 {@link #peek peek} 不同之处在在于如
* 果 deque 是空,它抛出一个异常。
*
* 这个方法等价于 {@link #getFirst}。
*/
public E element() {
return getFirst(); //#getFirst
}
/**
* 返回,但是不移除,代表当前 deque 的 queue 的头,或者如果当前 deque 为空,则返回 {@code null}。
*
* 这个方法等价于 {@link #peekFirst}。
*/
public E peek() {
return peekFirst(); //#peekFirst
}
// *** 栈方法s ***
/**
* 向代表当前 deque 的栈推入一个元素。换句话说,在当前 deque 的前部插入一个元素。
*
* 这个方法等价于 {@link #addFirst}。
*/
public void push(E e) {
addFirst(e); //#addFirst
}
/**
* 从代表当前 deque 的栈顶弹出一个元素。换句话说,移除并返回当前 deque 的第一个元素。
*
* 这个方法等价于 {@link #removeFirst()}。
*/
public E pop() {
return removeFirst(); //#removeFirst
}
//检查不变量s,assert 关键字:如果检查结果为 true,程序继续运行,否则抛出 AssertionError 并终止运行。
private void checkInvariants() {
assert elements[tail] == null; //检查 elements tail 位置元素是否为 null
assert head == tail ? elements[head] == null : //检查 head 是否 == tail(head 如果是 null 那么是允许的)
(elements[head] != null && //检查 head 位置元素是否不为 null
elements[(tail - 1) & (elements.length - 1)] != null); //检查规化 tail - 1 位置元素不为 null
assert elements[(head - 1) & (elements.length - 1)] == null; //检查规化 head - 1 位置元素是否为 null
}
/**
*
* 移除这个元素s数组中指定位置的元素,如有需要调整头和尾。这会导致数组中的元素s向前或者向后移动。
*
* 这个方法被成为 delete 调用而不是 remove 来强调它的语义与那些 {@link List#remove(int)} 不同。
*/
private boolean delete(int i) {
checkInvariants(); //#checkInvariants
final Object[] elements = this.elements;
final int mask = elements.length - 1; //缓存 elements.length - 1
final int h = head;
final int t = tail;
final int front = (i - h) & mask; //前部,符合 head 的语义,i - h 小于等于 elements.length - 1 时返回自己,大于 elements.length - 1 时为 0
final int back = (t - i) & mask; //后部,符合 tail 的语义
// 不变量:头 <= i < 尾的模环
/**
* t - h 小于等于 elements - 1 时返回自己,大于 elements.length - 1 时候返回 0,所以出现
* front 大于等 ((t - h) & mask)) 等情况就是 i > t 并且 i - h 小于 elements.length - 1
* 或者 i - h 大于 mask 并且 t - h 也大于 mask 两种情况
**/
if (front >= ((t - h) & mask))
throw new ConcurrentModificationException(); //抛出 ConcurrentModificationException 异常
// 对于最少元素移动的优化
if (front < back) { //如果 front 小于 back,这里应该是元素语义靠后的意思(head 不一定真的在 tail 前面)
if (h <= i) { //如果 head 小于等于参数 i
System.arraycopy(elements, h, elements, h + 1, front); //进行拷贝,从 elemnts 中 h 到 h + 1 位置的元素,长度为 front,替换 elements 中的元素
} else { // head 大于参数 i 环绕
System.arraycopy(elements, 0, elements, 1, i); //进行拷贝,从 elements 中 0 到 1 位置的元素,长度为 i,替换 elements 中的元素
elements[0] = elements[mask]; //elements length - 1 位置的元素赋值给 elements 0 位置
System.arraycopy(elements, h, elements, h + 1, mask - h); //进行拷贝,从 elements h 到 h + 1 位置的元素,长度为 mask - h,替换 elements 中的元素
}
elements[h] = null; //清空插槽
head = (h + 1) & mask; //规化递增 head
return false; //返回 false
} else { //如果 front 大于等于 back,语义靠前
if (i < t) { // 如果 i 小于 tail,也要拷贝尾部 null 的元素
System.arraycopy(elements, i + 1, elements, i, back); //进行拷贝,从 i + 1 到 i 位置,长度为 back,替换 elements 中的元素
tail = t - 1; //递减 tail
} else { // i 大于 tail,环绕
System.arraycopy(elements, i + 1, elements, i, mask - i); //进行拷贝,从 i + 1 到 i 的位置
elements[mask] = elements[0]; //elements 0 位置的元素赋值给 elements length - 1 位置
System.arraycopy(elements, 1, elements, 0, t); //进行拷贝,从 1 到 0 位置,长度为 t,替换 elements 中的元素
tail = (t - 1) & mask; //规化递减 tail
}
return true; //返回 true
}
}
// *** 集合方法s ***
/**
* 返回当前 deque 中的元素数量。
*/
public int size() {
/**
* 规化 tail - head,由于 head 与 tail 一定在 element.length 中,所
* 以 tail - head 的模一定小于等于 elements.length - 1
* (1)假设 tail - head 大于零,返回的就是 tail - head
* (2)反之如果 tail - head 小于零返回的就是 elements.length - 1
* (3)如果 tail - head 等于 0 返回值就是 0
**/
return (tail - head) & (elements.length - 1);
}
/**
* 如果当前 deque 不包含任何元素则返回 {@code true}。
*/
public boolean isEmpty() {
return head == tail;
}
/**
* 获得一个涵盖当前 deque 中所有元素的迭代器。元素s将从第一个(头)被排序到最后一个(尾)。这也是元素将
* 被出列的顺序(通过连续调用 {@link #remove} 或者弹出(通过连续调用 ){@link #pop})。
*/
public Iterator<E> iterator() {
return new DeqIterator(); //返回 DeqIterator 的构造器
}
//获得一个倒序迭代器
public Iterator<E> descendingIterator() {
return new DescendingIterator(); //返回 DescendingIterator 的构造器
}
//DeqIterator 类,实现了 Iterator 接口
private class DeqIterator implements Iterator<E> {
/**
* 下一次调用 next 要返回的元素的位置。
*/
private int cursor = head; //游标,初始化为 head
/**
* 构造时记录的尾(也在 remove 中),来停止迭代器并且检查并行修改操作。
*/
private int fence = tail; //栅,初始化为 tail
/**
* 最近一次调用 next 返回的元素的位置。如果元素被通过一个 remove 调用删除了,重置为 -1。
*/
private int lastRet = -1; //初始化为 -1
//判断游标之后是否还存在元素方法
public boolean hasNext() {
return cursor != fence; //判断游标是否不等于栅
}
//返回游标之后的下一个元素方法
public E next() {
if (cursor == fence) //如果游标 == 栅
throw new NoSuchElementException(); //抛出 NoSuchElementException
@SuppressWarnings("unchecked")
E result = (E) elements[cursor]; //找到 elements 游标位置元素
// 这个检查不会捕获所有可能的并行修改操作s,
// 但确实捕获了(那些)破坏遍历的
if (tail != fence || result == null) //如果 tail 不等于栅或者 result 为 null(被移除)
throw new ConcurrentModificationException(); //抛出 ConcurrentModificationException
lastRet = cursor; //cursor 赋值给 lastRet
cursor = (cursor + 1) & (elements.length - 1); //规化递增 cursor
return result; //返回 result
}
//移除操作
public void remove() {
if (lastRet < 0) //如果 lastRet 小于 0(被重置了)
throw new IllegalStateException(); //抛出 IllegalStateException
if (delete(lastRet)) { // #delete,如果左移,撤销 next() 中的增量
cursor = (cursor - 1) & (elements.length - 1); //规化递减游标
fence = tail; //tail 赋值给 fence
}
lastRet = -1; //重置 lastRet
}
//循环消费
public void forEachRemaining(Consumer<? super E> action) {
Objects.requireNonNull(action);
Object[] a = elements;
int m = a.length - 1, f = fence, i = cursor; //m 为 length - 1,f 为栅,i 为游标
cursor = f; //更新 cursor 为栅
while (i != f) { //循环当游标不等于栅时
@SuppressWarnings("unchecked") E e = (E)a[i]; //获取游标位置元素
i = (i + 1) & m; //规化递增游标
if (e == null)
throw new ConcurrentModificationException(); //如果元素为 null(可能被 remove),抛出 ConcurrentModificationException
action.accept(e); //消费元素
}
}
}
//DescendingIterator 类,实现了 Iterator 接口
private class DescendingIterator implements Iterator<E> {
/*
* 这个类差不多是 DeqIterator 的一个镜像,使用 tail 而不是 head 来初始化游标,并且用 head 而不
* 是 tail 来初始化栅。
*/
private int cursor = tail; //游标,初始化为 tail
private int fence = head; //栅,初始化为 head
private int lastRet = -1;
//判断是否游标之后还有元素方法
public boolean hasNext() {
return cursor != fence;
}
//获取游标之后的元素方法
public E next() {
if (cursor == fence)
throw new NoSuchElementException();
//这里与其他规化递减 tail 的方法相同
cursor = (cursor - 1) & (elements.length - 1);
@SuppressWarnings("unchecked")
E result = (E) elements[cursor];
if (head != fence || result == null)
throw new ConcurrentModificationException();
lastRet = cursor;
return result;
}
//移除方法
public void remove() {
if (lastRet < 0)
throw new IllegalStateException();
if (!delete(lastRet)) {
cursor = (cursor + 1) & (elements.length - 1);
fence = head;
}
lastRet = -1;
}
//这个类中没有实现 forEachRemaining 循环消费方法
}
/**
* 如果当前 deque 包含指定的元素则返回 {@code true}。
*
* 更正式地说,当前仅当当前 deque 包含至少一个符合 {@code o.equals(e)} 的元素 {@code e} 时返回
* {@code true}。
*/
public boolean contains(Object o) {
if (o == null)
return false;
int mask = elements.length - 1;
int i = head;
Object x;
while ( (x = elements[i]) != null) { //循环判断 elements i 位置元素是否不为 null
if (o.equals(x)) //如果 x 与参数 o equals
return true; //返回 true
i = (i + 1) & mask; //规化递增 i
}
return false; //返回 false
}
/**
* 从当前 deque 中移除一个指定元素的单个实例。如果这个 deque 不包含这样的元素,它不会被修改。
*
* 更正式地说,移除第一个符合 {@code o.equals(e)} 的元素 {@code e}(如果存在这样的一个元素)。
*
* 如果当前 deque 包含指定元素(或者等价的,如果当前 deque 被修改了作为调用的返回值),返回 {@code
* true}。
*/
public boolean remove(Object o) {
return removeFirstOccurrence(o); //#removeFirstOccurrence
}
/**
* 移除当前 deque 中的所有元素s。这个 deque 将在调用之后变成空。
*/
public void clear() {
int h = head;
int t = tail;
if (h != t) { // 判断有元素,清楚所有元素
head = tail = 0; //重置 head 与tail
int i = h;
int mask = elements.length - 1;
do {
elements[i] = null; //清空 elements i 位置插槽
i = (i + 1) & mask; //规化递增 i
} while (i != t); //循环如果 i != t
}
}
/**
* 返回包含当前 deque 中所有元素s的一个数组(从第一个到最后一个元素)。
*
* 返回的数组将是“安全的”因为当前 deque 不维护它的引用。(换句话说,这个方法必须分配一个新的数组。)
* 调用这因而可以自由地修改返回的数组。
*
* 这个方法操作起来就像基于数组与基于 collection APIs 的一个桥梁。
*/
public Object[] toArray() {
return copyElements(new Object[size()]); //#copyElements
}
/**
* 以正确的顺序返回一个包含了当前 deque 中所有元素的数组(从第一个到最后一个元素),这个返回数组的运
* 行时类型根据指定数组类型而定。如果这个 deque 合适(放在)指定数组中,它在其中返回。不然的话,一个
* 当前 deque 长度的新数组 被分配为与指定数组类型相同的运行时类型。
*
* 如果指定数组的空间合适这个 deque (的唱度)(比如,这个数组有比当前 deque 更多的元素),数组中紧
* 跟在 deque 最后的元素被置为 {@code null}。
*
* 就像 {@link #toArray()} 方法,这个方法以基于数组和基于 collection APIs 的桥梁的样子运作。并
* 且,这个方法允许精准可控制返回数组的运行时类型,而且可能,在某些情况下,被用来节省分配操作开销s。
*
* 假设 {@code x} 是一个已经只保存 strings 的 deque。一下的代码可以被用来向一个新分配的 {@code
* String} 数组中倾倒 deque:
*
* {@code String[] y = x.toArray(new String[0]);}
*
* 注意 {@code toArray(new Object[0])} 在功能是与 {@code toArray()} 相同的。
*/
@SuppressWarnings("unchecked")
public <T> T[] toArray(T[] a) {
int size = size(); //#size
if (a.length < size) //如果参数的长度小于 size
a = (T[])java.lang.reflect.Array.newInstance(
a.getClass().getComponentType(), size); //分配新数组
copyElements(a); //#copyElements
if (a.length > size) //如果参数的长度大于 size
a[size] = null; //参数数组的 size 位置置为 null
return a; //返回 a
}
// *** Object 方法s ***
/**
* 返回当前 deque 的一个拷贝。
*/
public ArrayDeque<E> clone() {
try {
@SuppressWarnings("unchecked")
ArrayDeque<E> resul t = (ArrayDeque<E>) super.clone(); //Object#clone
result.elements = Arrays.copyOf(elements, elements.length); //调用 Arrays.copyOf 方法,分配一个新数组
return result; //返回 result
} catch (CloneNotSupportedException e) {
throw new AssertionError();
}
}
private static final long serialVersionUID = 2340985798034038923L;
/**
* 序列化写方法
*
* 保存当前 deque 到一个流(意味着,序列化它)。
*/
private void writeObject(java.io.ObjectOutputStream s)
throws java.io.IOException {
s.defaultWriteObject();
// 写出长度
s.writeInt(size());
// 按顺序写出元素s
int mask = elements.length - 1;
for (int i = head; i != tail; i = (i + 1) & mask)
s.writeObject(elements[i]);
}
/**
* 序列化读方法
*
* 从一个流中重构 deque(意味着,反序列化它)。
*/
private void readObject(java.io.ObjectInputStream s)
throws java.io.IOException, ClassNotFoundException {
s.defaultReadObject();
// 读入长度并且分配数组
int size = s.readInt();
int capacity = calculateSize(size);
SharedSecrets.getJavaOISAccess().checkArray(s, Object[].class, capacity);
allocateElements(size);
head = 0;
tail = size;
// 按正确的顺序读入所有元素s
for (int i = 0; i < size; i++)
elements[i] = s.readObject();
}
/**
* 构造一个延迟绑定和 fail-fast 的包含当前 deque 中所有元素的 {@link Spliterator}。
*
* 这个 {@code Spliterator} 记录了 {@link Spliterator#SIZED},{@link
* Spliterator#SUBSIZED},{@link Spliterator#ORDERED} 和 {@link Spliterator#NONNULL}
* 特征值。重写的实现类s应该对于额外的特征值进行记录。
*/
public Spliterator<E> spliterator() {
return new DeqSpliterator<E>(this, -1, -1); //调用 DeqSpliterator 构造器
}
//DeqSpliterator 类,实现了 Spliterator 接口
static final class DeqSpliterator<E> implements Spliterator<E> {
private final ArrayDeque<E> deq;
private int fence; // 直到 first 被时候前都是 -1
private int index; // 当前位置,在遍历/分割时被修改
/**构造一个涵盖指定数组和范围的新的并行迭代器**/
DeqSpliterator(ArrayDeque<E> deq, int origin, int fence) {
this.deq = deq;
this.index = origin;
this.fence = fence;
}
//获取栅方法
private int getFence() { // 强制初始化
int t;
if ((t = fence) < 0) {
t = fence = deq.tail;
index = deq.head;
}
return t;
}
//尝试分割方法
public DeqSpliterator<E> trySplit() {
int t = getFence(), h = index, n = deq.elements.length;
if (h != t && ((h + 1) & (n - 1)) != t) {
if (h > t)
t += n;
int m = ((h + t) >>> 1) & (n - 1);
return new DeqSpliterator<>(deq, h, index = m);
}
return null;
}
//循环消费方法
public void forEachRemaining(Consumer<? super E> consumer) {
if (consumer == null)
throw new NullPointerException();
Object[] a = deq.elements;
int m = a.length - 1, f = getFence(), i = index;
index = f;
while (i != f) {
@SuppressWarnings("unchecked") E e = (E)a[i];
i = (i + 1) & m;
if (e == null)
throw new ConcurrentModificationException();
consumer.accept(e);
}
}
//进一步尝试消费剩余元素
public boolean tryAdvance(Consumer<? super E> consumer) {
if (consumer == null)
throw new NullPointerException();
Object[] a = deq.elements;
int m = a.length - 1, f = getFence(), i = index;
if (i != fence) {
@SuppressWarnings("unchecked") E e = (E)a[i];
index = (i + 1) & m;
if (e == null)
throw new ConcurrentModificationException();
consumer.accept(e);
return true;
}
return false;
}
//估算长度方法
public long estimateSize() {
int n = getFence() - index;
if (n < 0)
n += deq.elements.length;
return (long) n;
}
//获取特征值方法
@Override
public int characteristics() {
return Spliterator.ORDERED | Spliterator.SIZED |
Spliterator.NONNULL | Spliterator.SUBSIZED;
}
}
}
通过 ArrayDeque 的源码,可以来回答先前提出的两个问题了:
1、某种操作在导致 head 或者 tail 超出了数组长度时该如何处理?
通过“规化”位与操作与首尾位置判断来控制,所谓的“规化”操作就是 ArrayDeque 的核心代码:x & (length - 1)。由于 length 一定是 2 的幂次方,假设 length 是 2 的 n 次方,length - 1 的二进制数码一定是末尾 n - 1 为都为 1,这就使得对于 head,当 head 大于 0 并且小于等于 length - 1 时候保持原有,而大于 length - 1 时候就是 0,如果小于 0 的话(只有为 -1)就是 length - 1,对于 tail 也是同理,这样小于逻辑 0 时就会回到物理尾,大于数组长度时又会回到物理头,通过一个 & 完美解决了问题。
2、何时对数组进行扩容?
假设以通过默认构造器创建一个 ArrayDeque 对象,那么它的长度为 16,head 与 tail 是相同的都为 0,在加入第一个元素后 head 就与 tail 不同了,比如通过 addFirst 方法加入一个元素时,head = -1 & 15,head 就是 15,而此时 tail 还是 0(head 大于 tail),将这次数组分配称为第 0 次扩容。此后无论是对于容器本身的操作还是通过迭代器操作都有可能改变 head 或者 tail 的值,而当下一次 head == tail 的时候,就认为发生了缠绕(从语义上也很好理解,首尾相连),就会对数组进行扩容。
另外通过源码还可以发现,整个 ArrayDeque 中基本上都是对于首(head)和尾(tail)的操作,唯有一个 delete 方法允许传入一个位置参数(从语义上是删除这个位置的元素),这也是除了扩容与拷贝之外唯一会发生 System.arrarycopy(批量移动) 的方法,这个方法首先限制了 i 必须在 head 与 tail 之间,然后判断 i 是更靠近 haed 还是 tail(性能考虑),如果 h <= i 说明逻辑顺序与物理顺序相同,只需要调用一次 System.arraycopy,否则说明出现了分开的两段,则需要调用两次 System.arraycopy。
它对于迭代器的时候也与其他数据结构(例如 ArrayList)有些许不同,其他数据结构的迭代器通常是通过构造方法来对自己的某些属性(比如游标)赋值,而它是通过直接对类属性赋默认值来实现的。
以上就是对于 ArrayDeque 的介绍与分析,下一篇将对 WeakHashMap 进行介绍与分析。