SVRG&Lissa&NewSamp实现

SVRG, NewSamp & Lissa 实现

---

具体实现参见Github,算法分析可以参我的一篇二阶算法博客

SVRG, NewSamp & Lissa

这是基于python实现的SVRG, NewSamp, Lissa的baseline.
数据集采用的是Mnist49(手写数据集中的4和9)

SVRG

算法分析

SVRG（Stochastic Variance Reduced Gradient）算法主要是通过对梯度进行Variance Reduced。SVRG是近几年中随机梯度下降算法中很典型的算法，在每个迭代周期开始的时，先计算当前迭代值$w_k$下批量的平均梯度$\nabla R_n({\omega }_k)$。而内层以j为下标的m次循环进行如下更新
$$g_j\leftarrow \nabla f_{i_j}({\omega }_j)-(\nabla f_{i_j}({\omega }_k)-\nabla R_n({\omega }_k))$$
其中$i_j $是1n中随机选取的下标。这个公式有一个简单的解释，$\nabla f_{i_j } (ω_k )$的期望等于$\nabla R_n (ω_k )$，那么他们的差就相当于该样本上估计$\nabla f_{i_j } (ω_k )$的偏差，那么当前的随机梯度估计减去这个偏差便可以矫正为更准确的估计。

当实际应用中要求精确的训练精度时，相对于SG算法，SVRG展现相当有效的收敛性质。在第一个epoch的迭代中，SG算法更加有效，但是随着迭代的增加SVRG算法的优点就能够显现出来

核心实现

Logger.log("-------Svrg start---------")
while epoch_cnt < self.epoch_num:
    u = self.get_gradient(w, self.train_x, self.train_y, self.alpha)
    epoch_cnt = epoch_cnt + 1
    wt = w
    for _ in range(m):
        t = t + 1
        idx = np.random.randint(n)
        data_x = self.train_x[:, idx]
        data_y = np.mat(self.train_y[:, idx])
        delta = self.get_gradient(wt, data_x, data_y, self.alpha) \
                - self.get_gradient(w, data_x, data_y, self.alpha)
        delta = delta + u
        wt = wt - self.step_size * delta

        if t % n == 0:
            epoch_cnt = epoch_cnt + 1
            # record the loss and epoch_cnt and time
    w = wt
Logger.log("---------Svrg end-------------")

NewSamp

算法分析

NewSamp他实质是基于子采样的牛顿法，是一个很简洁的算法。

1. 首先，NewSamp通过子采样避免对所有样本求Hessian。
2. 对于Hessian求逆. 牛顿法主要通过发掘Hessian的中所包含的曲率信息达到加速效果，由于重要的二阶曲率信息一般包含在最大的若干个特征值以及其对应的特征向量中。因而对于Hessian求逆的问题，NewSamp采用低秩矩阵近似技术来得到Hessian矩阵逆的近似。假如目标函数是凸函数，那么对应的Hessian矩阵特征值便是非负，对称的Hessian矩阵的奇异值和特征值相同，因而算法NewSamp采用截断SVD分解获得前k大的特征值以及对应特征向量, 然后快速得到Hessian的逆。

算法流程

核心实现

Logger.log("--------NewSamp start-------")
while np.linalg.norm(last_w - w, ord=2) >= eps:
    last_w = w
    # select data
    idx = np.random.choice(n, self.sample_size)
    data_x = self.train_x[:, idx]
    data_y = self.train_y[:, idx]
    # compute gradient and hessian
    grad = self.get_gradient(w, self.train_x, self.train_y, self.alpha)
    epoch_cnt = epoch_cnt + 1
    hessian = self.get_hessian(w, data_x, data_y, self.alpha)
    # TruncatedSVD
    u, s, v = svds(hessian, k=self.rank + 1)
    matrix_q = np.mat(np.eye(d)) / s[0] + np.mat(u[:, 1:]) * \
               (np.mat(np.diagflat(1 / s[1:])) - 1 / s[0] *                              np.mat(np.eye(self.rank))) * np.mat(v[1:, :])
    w = w - self.step_size * matrix_q * grad
    epoch_cnt = epoch_cnt + 1.0*self.sample_size/n
    # record the loss and epoch_cnt and time
# end while
Logger.log("NewSamp end")

Lissa

算法分析

LiSSA为二阶优化算法提出一种新颖的思路。NewSamp是对通过子采样估计出一个较为精确的Hessian，然后通过矩阵分解得出Hessian的逆的近似。

随机版本的L-BFGS则是基于拟牛顿思路，通过构造得出满足拟牛顿条件并和原Hessian的逆尽可能接近的矩阵。但是LiSSA则是通过对Hessian的逆的泰勒展开式，得出Hessian逆与Hessian的等式，再通过对Hessian的进行采样估计，来直接估计出Hessian的逆。LiSSA的思路完全不同于NewSamp和SLBFGS，同时LiSSA算法采用Hessian-vector product对形式因而对广义线性模型具有更加明显的优势。

核心实现

Logger.log("----------lissa start-------------")
while epoch_cnt < self.epoch_num:
    u = []
    grad = self.get_gradient(w, self.train_x, self.train_y, self.alpha)
    epoch_cnt = epoch_cnt + 1
    for i in range(self.s1):
        # set u[i] = grad
        u.append(grad)
        bt_sz = 1       #mini-batch size
        sz = int(self.s2/bt_sz)
        for _ in range(sz):
            tmp = np.mat(np.zeros((d, 1)))
            for k in range(bt_sz):
                idx = np.random.randint(n)
                data_x = self.train_x[:, idx]
                smj = np.asscalar(self.softmax(w.T * data_x))
                hessian_value = smj * (1 - smj)
                tmp = tmp + hessian_value * data_x * (data_x.T * u[i])
            tmp = tmp /bt_sz
            u[i] = (grad + u[i] - tmp)
        # end j
    # end i
    delta = np.mat(np.mean(u, axis=0))
    w = w - delta
    epoch_cnt = epoch_cnt + 1.0*(self.s1*self.s2)/n
    # record the loss and epoch_cnt and time
# end t
Logger.log("-------------Lissa end---------")

Lissa这里实现的时候,S2内部循环我用的是S2个样本的平均Hessian,因为使用随机Hessian发现迭代一次花费很长时间并且loss几乎不改变
第一次实验的时候，忽略了这里LiSSA对GLM广义线性模型可以加快速度,因为Hessian是秩一的,data_x * (data_x.T * u[i])只需要O(d)的复杂度，上述loss几乎不改变可能是stepSize的原因，后面实际实验发现效果还是可以的，但是有时会不收敛

功能解释

lodaData.py         #预处理数据集,并进行L2正则化
check.py            #检查Hessian和梯度计算是否正确
Algorithm.py        #求LR算法的Loss, 梯度, Hessian
AlgorithmFactory    #提供不同的算法,并产生随机的合适的参数
LR_Binary.py        #实现SVRG, Lissa, NewSamp的baseline
newSamp.py          # NewSamp算法的具体实现
liSSA.py            # LiSSA算法的具体实现
svrg.py             # SVRG算法的具体实现
main.py             #运行算法, 并选取相对最好的参数

实验参数

Lissa: T1:=1, S1:=1, S2:=7500, stepSize:=2
iteration number: 18.36, costTime: 6.19s
Svrg: m := 1, stepSize = 1.5
iteration number: 24, costTime: 17.8s
NewSamp: rank:=40, smapleSize:=2500, stepSize:=1
iteration number: 14.5, costTime: 1.24s

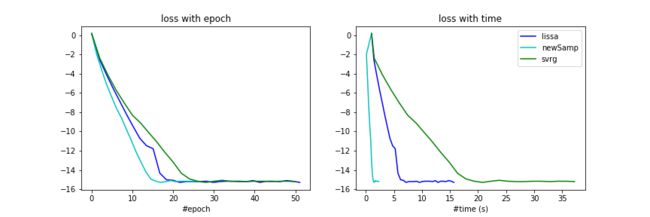
实验结果

from numpy import *
from pandas import *
import matplotlib.pyplot as plt

#获取实验结果, 并预处理处理
#最终显示log10(loss-bestLoss)与epoch和时间的对应关系
lissa_time = read_csv("./lissaWithBestTime.csv", header=None).T
newSamp_time = read_csv("./newSampWithBestTime.csv", header=None).T
svrg_time = read_csv("./svrgWithBestTime.csv", header=None).T
bestLoss = min(svrg_time[:][2].min(), newSamp_time[:][2].min())
bestLoss = min(lissa_time[:][2].min(), bestLoss)
bestLoss = bestLoss - 5e-16
lissa_time[:][2] = np.log10(lissa_time[:][2] - bestLoss)
svrg_time[:][2] = np.log10(svrg_time[:][2] - bestLoss)
newSamp_time[:][2] = np.log10(newSamp_time[:][2] - bestLoss)

画log(loss-bestLoss)和epoch&time的关系图

import matplotlib.pyplot as plt
fig = plt.figure(figsize=(12,4))
# plt.title('loss with epoch')
ax = fig.add_subplot(1, 2, 1)
ax.set_title("loss with epoch")
ax.set_xlabel("#epoch")
ax.plot(lissa_time[:][0], lissa_time[:][2], 'b-', label="lissa")
ax.plot(newSamp_time[:][0], newSamp_time[:][2],  'c-', label="newSamp")
ax.plot(svrg_time[:][0], svrg_time[:][2],  'g-', label="svrg")

ax = fig.add_subplot(1, 2, 2)
ax.set_title("loss with time")
ax.set_xlabel("#time (s)")
ax.plot(lissa_time[:][1], lissa_time[:][2], 'b-', label="lissa")
ax.plot(newSamp_time[:][1], newSamp_time[:][2],  'c-', label="newSamp")
ax.plot(svrg_time[:][1], svrg_time[:][2],  'g-', label="svrg")
plt.legend(loc='upper right')
plt.savefig("./result.png")
plt.show()

参考文献

1. Convergence rates of sub-sampled Newton methods
2. Second-Order Stochastic Optimization for Machine Learning in Linear Time
   3.Accelerating Stochastic Gradient Descent using Predictive Variance Reduction