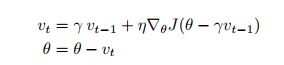梯度下降算法小结
梯度下降一类算法小结
标签(空格分隔): 梯度下降
以下内容为An overview of gradient descent optimization
algorithms读后笔记.
梯度下降算法变种
算法概览
最经典的梯度下降算法有:1.梯度下降(Batch gradient descent) 2. 随机梯度下降(Batch gradient descent) 3. mini-batch梯度下降(Mini-batch gradient descent)
算法的缺点
- Batch梯度下降, 当遍历计算整个数据集的梯度时候后, 对参数只进行了一次更新,梯度下降很可能变得很慢,同时对于数据集很大的时候内存可能不足.
- 随机梯度下降每次训练一个数据的时候就会更新一下参数.更新速度比1更快,同时1在更新的时候对相似的数据会存在计算冗余.
Batch gradient descent performs redundant computations for large datasets, as it recomputes gradients for similar examples before each parameter update. SGD does away with this redundancy by performing one update at a time.
- mini-batch梯度下降是1和2的折中,减少了参数更新时候的variance,一般mini-batch size设置为50-256.但是他不能保证很好的收敛性.
梯度下降的挑战
- 小的学习率导致学习慢, 大的学习率导致最优解附近波动
- 制定学习率表来动态调节, 这个表必须预先定义, 所以不能够捕捉到数据集的一些特征
- 所有参数都是相同的学习率, 如果数据很稀疏,特征都有着不同的频率, 就不能以相同的学习率来更新他们
- 当最小化非凸函数的时候, 会遇到很多次优解,必须防止无法跳出次优点.然而问题最大的就是马鞍点
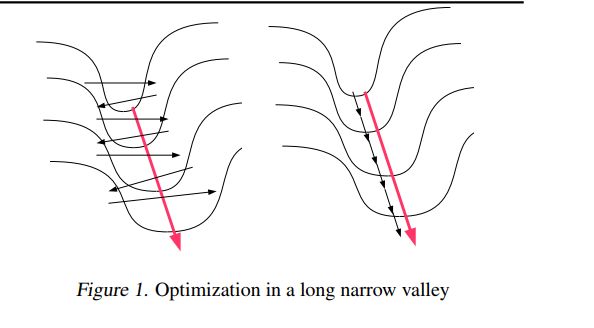
梯度下降的优化算法
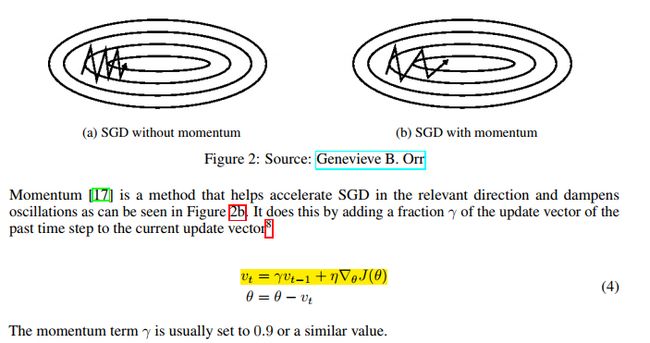
1. Momentum
2. NAG(Nesterov accelerated gradient )
带有预测的冲量, 想象一下快到最优解附近的时候,如果最优解附近梯度比较大,那么这里步伐就会很大导致很久才收敛,先预测未来的梯度来优化???还没有合理解释,显著增加了RNN的性能
3. Adagrad
之前所有参数的学习率都是相同的,这显然是不合理的,对于稀疏数据,对变化频率大的数据应该使用小的学习率,变化频率小的数据应该使用大的学习率

这里G是一个对角矩阵, G i i 是 θ t , i G_ii是\theta _{t,i} Gii是θt,i的根号和,这就能反应变化快慢
但是这个算法有一个缺点就是, 他的学习率是一直衰减的!!!
4. Adadelta
他是Adagrad算法的改进, 主要改进Adagrad算法的激进以及一直衰减的学习率
第二步,作者发现什么了???

假设空间之类的,在分子添加了RMS(delta)

5. RMSprop

这个算法是Hinton自己独立想出来的一个算法,和上一个算法有着相同想法
6. Adam
这个算法和之前动量想法一样,分别构造了 g , g 2 g, g^2 g,g2的动量

同时为了无偏估计,除以了一个系数
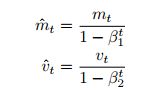
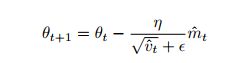
7. AdaMax
对Adam分母V_t进行了泛化,原来的形式相当于L2正则,现在改为LP正则,并让p趋于无穷大

8. Nadam
这里Dozat修改了NAG的算法,将原来对梯度提前的预估改为对动量的预估

这里NAG2在和最原始的冲量对比,发现只是修改了对比the momentum update rule 只是多一个梯度
那么将这种变化应用到Adam就可以得到Nadam
这里只是原本t-1时刻m的估计改为t时刻m的估计
参考文献
- An overview of gradient descent optimization algorithms
- Deep learning via Hessian-free optimization