机器学习十大经典算法之逻辑回归
逻辑回归简介
逻辑回归虽然名称有回归两字,但是用来做分类算法的,大家都熟悉线性回归,一般形式是 Y = a X + b Y=aX+b Y=aX+b,y的取值范围是[-∞, +∞]。因其简单而受到工业界的关注。
Y的取值范围过大,一般要把结果进行正则化,限定在[0,1]。所以需要把结果带入非线性变换Sigmoid函数中,即可得到[0,1]之间取值范围的数S,S可以把它看成是一个概率值,如果我们设置概率阈值为0.5,那么S大于0.5可以看成是正样本,小于0.5看成是负样本,就可以进行分类了。
Sigmoid函数
做过机器学习或是深度学习的小伙伴们都知道,sigmoid函数一般都是接在卷积神经网络层或是其正则化层之后,作为激活函数,相当于人类神经系统的突触传递。其数学表达式如下:
函数中t无论取什么值,其结果都在[0,-1]的区间内。即一个分类问题就有两种答案,一种是“是”,一种是“否”,那0对应着“否”,1对应着“是”。我们可以假设分类的阈值是0.5,结果大于0.5的归为一个分类,小于0.5的归为一个分类。阈值是可以自己设定的。
接下来我们把 a X + b aX+b aX+b带入t中就得到了我们的逻辑回归的一般模型方程:
结果P也可以理解为概率,换句话说概率大于0.5的属于1分类,概率小于0.5的属于0分类,这就达到了分类的目的。
逻辑回归分布
逻辑分布是一种连续型的概率分布,其分布函数和密度函数分别为:
F ( x ) = P ( X ≤ x ) = 1 1 + e − ( x − u ) / y F(x)=P(X\leq x)=\frac{1}{1+e^{-(x-u)/y}} F(x)=P(X≤x)=1+e−(x−u)/y1
f ( x ) = F ′ ( X ≤ x ) = e − ( x − u ) / y y ( 1 + e − ( x − u ) / y ) 2 f(x)={F}'(X\leq x)=\frac{e^{-(x-u)/y}}{y(1+e^{-(x-u)/y})2} f(x)=F′(X≤x)=y(1+e−(x−u)/y)2e−(x−u)/y
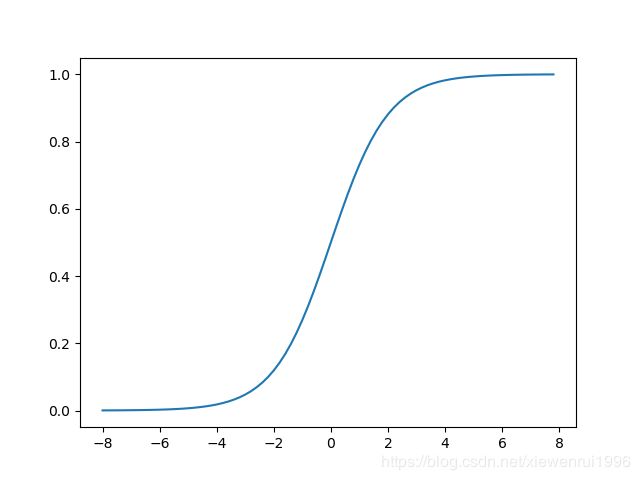
其中, u u u表示位置参数, γ \gamma γ为形状参数。我们可以看下其图像特征:
分布是由其位置和尺度参数定义的连续分布。逻辑分布的形状与正态分布的形状相似,但是逻辑分布的尾部更长,所以我们可以使用逻辑分布来建模比正态分布具有更长尾部和更高波峰的数据分布。在深度学习中常用到的 Sigmoid 函数就是逻辑的分布函数在 u = 0 , γ = 1 u=0,\gamma=1 u=0,γ=1的特殊形式。。
损失函数
逻辑回归的损失函数是 log loss,也就是对数似然函数,函数公式如下:
公式中的 y=1 表示的是真实值为1时用第一个公式,真实 y=0 用第二个公式计算损失。为什么要加上log函数呢?可以试想一下,当真实样本为1是,但h=0概率,那么log0=∞,这就对模型最大的惩罚力度;当h=1时,那么log1=0,相当于没有惩罚,也就是没有损失,达到最优结果。
在逻辑回归模型中,我们最大化似然函数和最小化损失函数实际上是等价的。
多分类逻辑回归
多分类逻辑回归思路步骤如下:
-
1.将类型class1看作正样本,其他类型全部看作负样本,然后我们就可以得到样本标记类型为该类型的概率p1。
-
2.再将另外类型class2看作正样本,其他类型全部看作负样本,同理得到p2。
-
3.以此循环,我们可以得到该待预测样本的标记类型分别为类型class i时的概率pi,最后我们取pi中最大的那个概率对应的样本标记类型作为我们的待预测样本类型。
总之还是以二分类来依次划分,并求出最大概率结果。
逻辑回归优点
- LR能以概率的形式输出结果,而非只是0,1判定。
- LR的可解释性强,可控度高。
- 训练快,feature engineering之后效果赞。
- 因为结果是概率,可以做ranking model。
逻辑回归常用的优化方法
一阶方法
梯度下降、随机梯度下降、mini 随机梯度下降降法。随机梯度下降不但速度上比原始梯度下降要快,局部最优化问题时可以一定程度上抑制局部最优解的发生。
逻辑回归的损失函数如下:
J ( w ) = − 1 n ( ∑ i = 1 n y i l n p ( x i ) + ( 1 − y i ) ( l n ( 1 − p ( x i ) ) ) J(w)=-\frac{1}{n}(\sum_{i=1}^{n}y_{i}lnp(x_{i})+(1-y_{i})(ln(1-p(x_{i}))) J(w)=−n1(∑i=1nyilnp(xi)+(1−yi)(ln(1−p(xi)))
梯度下降是通过 J ( w ) J(w) J(w) 对 w w w的一阶导数来找下降方向,并且以迭代的方式来更新参数,更新方式为:
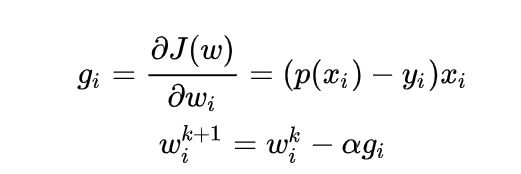
其中 k 为迭代次数。每次更新参数后,可以通过比较 ∥ J ( w k + 1 ) − J ( w k ) ∥ \left \| J(w^{k+1})- J(w^{k})\right \| ∥∥J(wk+1)−J(wk)∥∥小于阈值或者到达最大迭代次数来停止迭代。
二阶方法:牛顿法
牛顿法其实就是通过切线与x轴的交点不断更新切线的位置,直到达到曲线与x轴的交点得到方程解。在实际应用中我们因为常常要求解凸优化问题,也就是要求解函数一阶导数为0的位置,而牛顿法恰好可以给这种问题提供解决方法。
牛顿法首先选择一个点作为起始点,并进行一次二阶泰勒展开得到导数为0的点进行一个更新,直到达到要求,这时牛顿法也就成了二阶求解问题,比一阶方法更快。我们常常看到的x通常为一个多维向量,这也就引出了Hessian矩阵的概念(就是x的二阶导数矩阵)。
缺点:牛顿法是定长迭代,没有步长因子,所以不能保证函数值稳定的下降,严重时甚至会失败。还有就是牛顿法要求函数一定是二阶可导的。而且计算Hessian矩阵的逆复杂度很大。
逻辑斯特回归为什么要对特征进行离散化
- 逻辑回归属于广义线性模型,表达能力受限;单变量离散化为N个后,每个变量有单独的权重,相当于为模型引入了非线性,能够提升模型表达能力,加大拟合;
- 鲁棒性。离散化后的特征对异常数据有很强的鲁棒性:比如一个特征是年龄>30是1,否则0。如果特征没有离散化,一个异常数据“年龄300岁”会给模型造成很大的干扰;
- 方便交叉与特征组合:离散化后可以进行特征交叉,由M+N个变量变为M*N个变量,进一步引入非线性,提升表达能力;
- 简化模型:特征离散化以后,起到了简化了逻辑回归模型的作用,降低了模型过拟合的风险。
代码实现
https://github.com/Jack-Cherish/Machine-Learning
参考文献
https://zhuanlan.zhihu.com/p/74874291
https://zhuanlan.zhihu.com/p/73608677