SLAM的一些学习笔记

目录

一．基础概念

1）关于Hx=g方程中

没有位姿与位姿的约束

H为什么是J的转置乘以J

2)关于雅克比矩阵：

2.1）所谓增量方程系数的路标部分为什么是对角阵

3）所谓边缘化

4）邻接矩阵(Adjacency Matrix)

5）关于非线性优化定位和稠密建图的深度滤波器

6）上采样和下采样

7）专有名词

二．各个开源代码

2.1 dso

前后端

滑动窗口 

边缘化

DSO的大致流程

FEJ零空间

Jacobi矩阵导数推导

2.2 LSD

2.3 orb-slam

关于orb-slam的BA：

关于回环检测

2.4 SVO

三．有关语义

１)关于图像识别和图像分割

---

一．基础概念

1）关于Hx=g方程中

没有位姿与位姿的约束

背景：B矩阵代表左上角位姿对角阵，C代表右下角特征点对角阵。

其中H=J的转置*J（J是雅克比矩阵）J的每一行都是由偏导数组成的，对于一个位姿T1观察到地图点P1的事件来说，J11的这一行，除了J11对T1的偏导数，J11对P1的偏导数，其余全为0（系统中还有别的T和P）

心得：在J矩阵中，为什么没有对T1和T2再进行约束了，我想原因是：T1和T2的共视点已经表示出了这种约束关系。其实对于视觉定位来说，本身位姿就是由共视点来计算的，所以不需要在BA中再体现位姿之间的关系了。

所谓的回环检测也是一样的 就是当前帧和回环帧有共视点了 这就是回环检测做的约束，而且在回环检测全局优化当中，当前帧和回环帧是不动的 所以误差才被传递了。（当前帧会在全局优化前被重新求解）

H为什么是J的转置乘以J

我不知道我这一点我在写什么，随便瞎写的 将来估计也看不懂了

在高斯牛顿法中是这样的，在别的优化方案中可能有变体，但是都与它息息相关。

在《十四讲》第六章先是推导了一阶和二阶梯度法，再来GN和LM法，看那个会有点想不通的原因是它指的是对f(x)求最小值，但是对于BA是一个代价函数，长相是 e-h(T,p)这样的，但是不管怎么都是最小值。沿着雅克比矩阵（一阶倒数很好想）的转置方向下降就是数学中沿着梯度下降的方法，其余的方法也能勉强想通。

2)关于雅克比矩阵：

基于特征点法的BA算法中 雅克比矩阵一般由两部分构成（视觉SLAM十四讲P247）

• 一部分是整体目标函数对相机姿态的偏导数
• 一部分是对路标点位置的偏导

目标函数即是 图像的二维像素位置与路标点经过相机外参数投影到像平面的位置之差的最小（可以有很多种方式表达比如范数）

这体现了SLAM的基本思想 同步获取姿态信息和地图 （地图在这里就是地图点了）

而在基于直接法的DSO中，雅可比由三部分组成（比一般的多一个）：

• 图像雅可比，即图像梯度；
• 几何雅可比，描述各量相对几何量，例如旋转和平移的变化率；
• 光度雅可比，描述各个量相对光度参数的雅可比；

（作者认为，几何和光度的雅可比，相对自变量来说通常是光滑函数；而图像雅可比则依赖图像数据，不够光滑；所以，在优化过程中，几何和光度的雅可比仅在迭代开始时计算一次，此后固定不变[1]。而图像雅可比则随着迭代更新。这种做法称为First-Estimate-Jacobian（FEJ），在VIO中也会经常用到[8]。它可以减小计算量、防止优化往错误的地方走太多，也可以在边缘化过程中保证零空间的维度不会降低，后者我们还要在后文继续谈。）

这是因为直接法的原理造成的 在基于直接法的SLAM当中，甚至地图都不可重复利用，地图只是在运动中绘制出的周围环境罢了，所以目标函数？还不太清楚 再看一下

2.1）关于增量方程系数的路标部分是对角阵 

• 有人会把增量方程的系数称作Hessian矩阵（下面我也会这么说），不过也有道理，毕竟在＜牛顿法＞当中就是Hessian矩阵，但是GN法把这个改成简单的J转置J了．然后LM法又添加了一个小东西．
• 关于雅可比矩阵和S矩阵．注意到一般的增量方程如果使用schur消元，那么一直利用的都是路标部分的对角阵的逆非常好求解的特性．而S矩阵则表明了两个相机之间的共视关系．
• 为什么增量方程系数的路标部分一般是是对角阵呢？注意，这是大多数情况下的，dso就不是．

大多数情况：采用最小几何误差方法．将一个已经计算出来的三维点重投影到当前这个帧上，对比重投影出来的二维坐标和实际上图片的二维坐标，得出误差．后续通过迭代的方法，不断计算增量并改变相机位姿和三维点的位置，来起到减小误差的作用．

这个小误差所涉及到的东西为：一个三维点(x,y,z)，当前帧图像(当前相机外参)，相机内参？，注意哦！一个误差只涉及到一个帧，也就是一个相机位姿．所以是对角阵！

dso等的情况：采用最小光度误差的方法，他直接在哪里呢？不要三维点，我直接这个像素点利用逆深度信息反投影到空间再投影到下个帧．

那么这样的话，这个点就一定需要一个主导帧（host frame），然后我又要投影到新的帧上，所以一个点对应着两个帧，和一个逆深度信息．所以Hessian矩阵中的位姿部分就不是对角阵啦，但是能不能代表共视关系呢？？？不管怎样，我计算Schur消元不在乎他是不是对角阵，只要路标部分是对角阵就好啦（没有几何先验，也就是不稠密，或者稠密但是忽视或者近似）！

• PS: 一个dso误差涉及到:1)这个点的逆深度信息；2)相机内参；3)两个帧的位姿；4)光度传递函数的４个系数

3）所谓边缘化

从概率角度来看,我们称这一步为边缘化,是因为我们实际上把求 (∆x c , ∆x p ) （位姿，路标）的问题,转化成先求 ∆x c ,再求 ∆x p 的过程。这一步相当于做了条件概率展开:
　　　　　　　　　　　P (x c , x p ) = P (x c ) · P (x p |x c ).
结果是求出了关于 x c 的边缘分布,故称边缘化。在上边讲的边缘化过程中,我们实际把所有的路标点都给边缘化了。

刚开始把路标那部分先消去，所以边缘化了路标，求出了位姿的边缘分布．

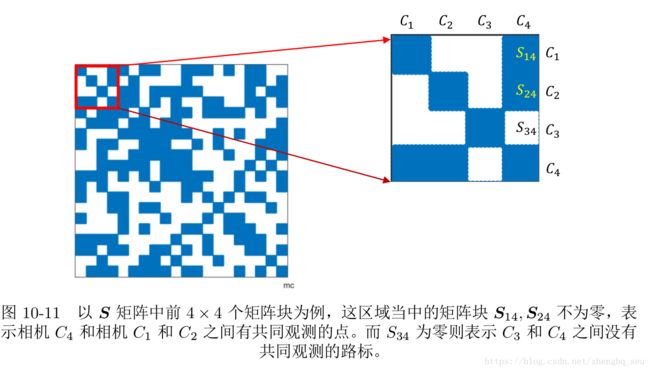
4）邻接矩阵(Adjacency Matrix)

所谓邻接矩阵是这样一种矩阵,它的第 i, j 个元素描述了节点 i 和 j 是否存在一条边。如果存在此边,设这个元素为 1,否则设为 0。

上面的 H 矩阵一共有 8 × 8 个矩阵块,对于 H 矩阵当中处于非对角线的矩阵块来说,如果该矩阵块非零,则其位置所对应的变量之间会在图中存在一条边．

所以,H 矩阵当中的非对角部分的非零矩阵块可以理解为它对应的两个变量之间存在联系,或者可以称之为约束。于是,我们发现图优化结构与增量方程的稀疏性存在着明显的联系。

5）关于非线性优化定位和稠密建图的深度滤波器

在相机定位中，非线性优化考虑之前所有时刻的姿态信息，而滤波器只考虑上一个时刻的状态，即马尔科夫性．

非线性优化的一般使用场景：前端的特征稀疏地图和相机粗糙位姿获取之后，在后端采用非线性优化优化所有变量（类比与orb的全局优化）

用与相机位姿求解的滤波器不加考虑了，因为这个方法精度不高．

深度滤波器：用于稠密建图的深度图估计

估计稠密深度的一个完整的过程:

1. 假设所有像素的深度满足某个初始的高斯分布;

2. 当新数据产生时（新图像）,通过极线搜索和块匹配确定投影点位置;

3. 根据几何关系（还可以考虑光度不确定性）计算三角化后的深度以及不确定性（不确定性的计算完全是数学）;

4. 将当前观测融合进上一次的估计中（高斯和高斯相乘仍旧是高斯）。若收敛（低于阈值）则停止计算,否则返回 2。

6）上采样和下采样

缩小图像（或称为下采样（subsampled）或降采样（downsampled））的主要目的有两个：1、使得图像符合显示区域的大小；2、生成对应图像的缩略图。

放大图像（或称为上采样（upsampling）或图像插值（interpolating））的主要目的是放大原图像,从而可以显示在更高分辨率的显示设备上。

对图像的缩放操作并不能带来更多关于该图像的信息, 因此图像的质量将不可避免地受到影响。然而，确实有一些缩放方法能够增加图像的信息，从而使得缩放后的图像质量超过原图质量的。

7）专有名词

RMSE：均方根误差亦称标准误差

二．各个开源代码

• 2.1 dso

• 前后端

• 从后端来看，DSO使用一个由若干个关键帧组成的滑动窗口作为它的后端．这个窗口在整个VO过程中一直存在，并有一套方法来管理新数据的加入以及老数据的去除。后端除了维护这个窗口中的关键帧与地图点外，还会维护与优化相关的结构。特别地，这里指Gauss-Newton或Levenburg-Marquardt方法中的Hessian矩阵和b向量（仅先验部分）。当我们增加新的关键帧时，就必须扩展H和b的维度；反之，如果需要去掉某个关键帧（以及它携带的地图点）时，也需要降低H和b的维度。这个过程还需要将被删掉帧和点的信息，转移到窗口内剩余帧当中，这一步被称为边缘化（Marginalization）。
• 前端追踪部分，会通过一定的条件，来判断新来的帧是否可作为新的关键帧插入后端。同时，如果后端发现关键帧数已经大于窗口大小，也会通过特定的方法，选择其中一个帧进行去除。

 

• 滑动窗口 

dso里维护的滑动窗口其实就类似于orb的那个covisibility graph或者essential graph之类的．就是为了维持当前BA的维护的关键帧数量．

在Schur消元当中，也就是Marginalization.求解位姿部分的增量方程是主要的计算量（视觉slamP253)．那个方程的系数S的物理意义：S 矩阵的非对角线上的非零矩阵块,表示了该处对应的两个相机变量之间存在着共同观测的路标点,有时候称为共视(Co-visibility)。反之,如果该块为零,则表示这两个相机没有共同观测。

在实践当中,例如 ORB_SLAM中的 Local Mapping 环节,在做 BA 的时候刻意选择那些具有共同观测的帧作为关键帧,在这种情况下 Schur 消元后得到的 S 就是稠密矩阵。不过,由这个模块并不是实时执行,所以这种做法也是可以接受的。

但是在另一些方法里面,例如 DSO.OKVIS等,它们采用了滑动窗口方法(Sliding Window)。这类方法对每一帧都要求做一次 BA 来防止误差的累积,因此它们也必须采用一些技巧来保持 S 矩阵的稀疏性。

 

• 边缘化

Hessian矩阵在整个优化过程中都会一直维护于内存中。注意这种做法和ORB-SLAM2是不同的。在ORB-SLAM2的后端中，我们会不停地重构整个优化问题，求解，然后存储优化后的结果，但这个H矩阵是不会一直存在的。而在DSO中，由于H是一直维护的，所以之后的优化可以利用先前的结果，或者说，先前的优化为下一步提供了先验（Prior）。但是，为了维护这个H信息，DSO必须手动地增加/删除每一个帧和点，而不像ORB-SLAM2那样，可以无视帧和点的变化。

DSO在解BA时，边缘化了所有点的信息，计算优化的更新量。然而，与传统BA不同的是，DSO的左上角部分，即公式中的  ，并非为对角块，而是有先验的。传统BA中，这部分为对角块，主要原因是不知道相机运动的先验，而DSO的滑动窗口，则通过一定手段计算了这个先验。这里的先验主要来自两个部分（不懂？不确定．我以为是dso本身的＂点跟两个帧有关＂导致的B不对角）：

1. 边缘化某个点时，这个点的共视帧之间产生先验；
2. 边缘化某个帧时，在窗口内其他帧之间产生先验；

这里的“边缘化”，具体的操作和上面讲的边缘化，是一样的。也就是说，通过舒尔补，用矩阵的一部分去消元另一部分。然而实际操作的含义却有所不同。在BA的边缘化中，我们希望用边缘化加速整个问题的求解，但是解完问题后，这些帧和点仍旧是存在于窗口中的！而滑动窗口中的边缘化，是指我们不再需要这个点/这个帧。当它被边缘化时，我们将它的信息传递到了之后的先验中，而不会再利用这个点/这个帧了！请读者务必理清这层区别，否则在理解过程中会遇到问题。我们不妨将后者称为“永久边缘化”，以示区分。

• DSO的大致流程

• 对于非关键帧，DSO仅计算它的位姿，并用该帧图像更新每个未成熟点的深度估计；
• 后端仅处理关键帧部分的优化。除去一些内存维护操作，对每个关键帧主要做的处理有：增加新的残差项、去除错误的残差项、提取新未成熟点。
• 整个流程在一个线程内，但内部可能有多线程的操作。

 

• FEJ零空间

• 可在高博链接中细看

 

• Jacobi矩阵导数推导

• 先看十四讲的书再看这个

高博留下的问题，回头我来写！

• DSO是怎么初始化的？
• DSO的CoarseTracker如何估计新帧的位姿？
• 未成熟点是如何转换到正常地图点的？

• 2.2 LSD

LSD是开源软件中比较少见的纯相机dense的．求解增量函数的矩阵右下角也不是对角阵了（因为有几何先验，所以点点之间构造了联系），不是对角阵就没办法边缘化求解了，不知道具体是怎么求解BA的．很好奇．

 

• 2.3 orb-slam

• 关于orb-slam的BA：

• 全局BA：所有Map Point＋keyframe一起优化（除了第一帧KF固定
• 局部BA：根据convisibility graph选择局部区域进行优化．见链接．
• 运动BA：相机姿态优化，固定所有点（姿态优化，跟踪的时候使用，这不就是pose-graph优化吗，nice
• 方位图优化（小跑题）：类似于粗糙的全局优化近似，但实验证明更快，收敛也更好（好像是loop的最后essential graph optimization）

• 关于回环检测

• 如果某个回环帧对应的矩阵有足够多的内点，那去做Sim3优化。利用优化结果再去寻找更多的特征匹配，再做一遍优化。如果内点足够多，那么接受这个回环。
• 所谓sim3优化就是通过回环帧和待回环帧（反正就是那两个帧）的共视点来计算两帧的偏移位姿。然后对所有关键帧进行空间尺度矫正。
• 最后进行回环融合 （相对而言，我们更信任之前的信息而不是当前的信息。所以所谓的回环融合主要是把回环帧的信息融合到当前帧里面，包括匹配的特征点对应的三维信息（深度、尺度等））
• 和全局优化（固定回环帧及其邻域，当前帧及其邻域，优化剩余帧在世界坐标系的位姿）

from ORB-SLAM解析

单目SLAM一般都会发生尺度（scale）漂移，因此Sim3上的优化是必要的。相对于SE3，Sim3的自由度要多一个，而且优化的目标是矫正尺度因子，因此优化并没有加入更多的变量（如三维点）。作者在检测到闭环时在Sim3上对所有的位姿进行一次优化。定义Sim3上的残差如下：

ei,j=logSim3(SijSjwS−1iw）

其中 Siw的初值是尺度为1的Pos i相对于世界坐标系的变换矩阵。Si,j为Pos i和Pos j之间的（Sim3优化之前的）相对位姿矩阵，表示Siw和Sjw之间的测量（measurement）。此处相当于认为局部的相对位姿是准确的，而全局位姿有累计误差，是不准确的。

 

• 2.4 SVO

DSO是少数使用纯直接法（Fully direct）计算视觉里程计的系统之一。相比之下，SVO属于半直接法，仅在前端的Sparse model-based Image Alignment部分使用了直接法，之后的位姿估计、bundle adjustment，则仍旧使用传统的最小化重投影误差的方式。而ORB-SLAM2，则属于纯特征法，计算结果完全依赖特征匹配。

 

三．有关语义

１)关于图像识别和图像分割

我之前把这两个概念混淆了，看《Meaningful Maps With Object-Oriented Semantic Mapping》这篇文章的时候有所体会。SSD用于单帧图像识别，将场景地图转换为超体素然后加上CRF来分割。

当然这篇文章还有一些新颖的地方，虽然仍然没有用到端对端的神经网络，但是语义识别的层次已经到了物体级别，数据关联使用的是类ICP的方法。

顺便再记录一下《Incremental dense semantic stereo fusion for large-scale semantic scene reconstruction》的大致思路，在另一篇文章中对它的评价是“2015年，斯坦福的Vineet等人首次实现了一个接近实时的系统，能同时进行建图和语义分割，展示了把语义ＳＬＡＭ推向实用的可能性。但是这些方法采用的物体识别或者语义分割的方法都是基于传统工具的，”

大致思路：

Semantic Segmentation 采用的是 Random Forest（随机森林） 方法，具体我也没有细看，就不细表了。 

1.2 Mapping 
在 Mapping 这块，与传统的 3D Reconstruction 技术并没有什么不同，只是采用 Stereo 估计深度。该工作使用了 Voxel Hashing 实现的 KinectFusion 系统进行建图，以保证 Large-scale的重建。 
1.3 Semantic Fusion 
在这里我们点出了语义信息如何更好的帮助建图。此处利用语义信息来处理动态物体。我们知道，动态物体对于 tracking 和 fusion 都会有很大的影响。对于不同类物体，它是否是运动的概率是不一样的。比如车辆很可能是运动的，但是路面就肯定不是运动的。所以与传统的 KinectFusion 的 Fusion 方法不同， Semantic Fusion 利用语义信息根据 voxel 的 label给予每个 voxel 不同的 weight 进行 fusion。 
在更新方程中 是每个类 l 在 t 时间对于 voxel i的固定的 weight。 
1.4 Label Fusion 
我们在每一个 voxel 中存储对应 label 的概率，然后采用贝叶斯的方式用每次得到的 semantic map（在这里存储每个 pixel 对应 label 的概率）来更新每个 label 的概率。 
1.5 3D Condition Random Field 
在这一节简单的介绍一下 3D Condition Random Field。在这里我们把 Condition Random Field 定义在 voxel 上，所以从 2D Condition Random Field 扩展到了 3D Condition Random Field。 
loss function 由两部分组成： 
1. 对于每一个 voxel，我们定义一个 Unary potentials，也就是该 voxel 取得当前 label 所得到的 loss 
2. 对于相邻 voxel，我们定义 Pairwise potentials 施加 label 的一致性约束，期望得到smoothing 的结果。在这里，对于相同的 label，我们定义 loss 为 0，对于不同的 label 我们定义 loss 为 （公式不打了）
其中分别代表着 voxel 的位置， rgb 和法向的值。θ 代表的是不同量的权重。我们可以看到，差异越小， loss 越大。把上面两项加起来就得到了最终的 loss function，我们一般采用在 GPU 上并行的 meanfled 方法迭代求解出每个 voxel 的 label。 
【注意】每次的优化只是针对于当前的 frustum。