中缀表达式转后缀表达式 ---- 代码实现

在之前的文章中提到了中缀表达式转换为后缀表达式，但是只提及思想没有代码实现，今天粗略实现了一下。

先了解思想，代码在最下面。

中缀表达式转换为后缀表达式

1.创建栈
2.从左向右顺序获取中缀表达式

a.数字直接输出
b.运算符

遇到’ ( ‘直接入栈，遇到’ ) ‘将栈中‘ ( ‘之后入栈的全部输出，同时‘ ( ‘出栈但是不输出。其他符号将符号栈中的元素依次出栈并输出，直到遇到比当前符号优先级更低的符号或者’ ( ‘，将当前符号入栈。

3.获取完后，将栈中剩余的符号依次输出

例如：12 * (3 + 4) - 6 + 8 / 2
依次获取：
12 ，是数字，直接输出

后缀表达式:12
符号栈：

’ * ’ ，是运算符，入栈

后缀表达式:12
符号栈:*

’ ( ‘,左括号，直接入栈

后缀表达式：12
符号栈: * (

3 , 数字 ，输出

后缀表达式：12 3
符号栈: * (

‘ + ’，运算符 ，入栈

后缀表达式：12 3
符号栈: * ( +

4 ，数字，输出

后缀表达式：12 3 4
符号栈: * ( +

‘ ）’，右括号，栈中元素依次出栈并输出知道遇到左括号,并且左括号也要出栈且不输出

后缀表达式：12 3 4 +
符号栈: *

‘ - ’，操作符，减号的优先级低于乘号所以乘号出栈并输出，此时站内没有符号，减号入栈

后缀表达式：12 3 4 + *
符号栈: -

6 ，数字，输出

后缀表达式：12 3 4 + * 6
符号栈: -

’ + ‘,操作符 ，优先级与减号相同（也就是说没有减号的优先级高）所以减号出栈输出，加号入栈

后缀表达式：12 3 4 + * 6 -
符号栈: +

8 ，数字 ，输出

后缀表达式：12 3 4 + * 6 - 8
符号栈: +

‘ / ’，操作符，比减号的优先级高直接入栈

后缀表达式：12 3 4 + * 6 - 8
符号栈: + /

2 ，数字，输出

后缀表达式：12 3 4 + * 6 - 8 2
符号栈: + /
中缀表达式获取完后，将栈中剩余元素依次出栈输出
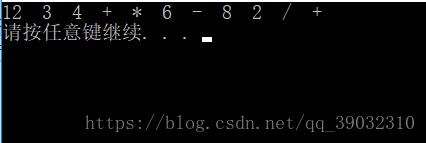
后缀表达式：12 3 4 + * 6 - 8 2 / +
符号栈:

以上就是中缀表达式转后缀表达式

/////MidTurnBack.h
#define max 10
typedef char DataType;
typedef struct Stack
{
    int top;
    DataType stack[max];
}Stack;

enum {Data,Ope,Left,Right} operate;

typedef struct Cell
{
    enum operate op;
    int data;
}cell;

////MidTurnBack.c
void MidTurnBack(cell* arr, int sz)
{
    Stack s;
    int i = 0;
    assert(arr);
    StackInit(&s);
    for (; i < sz; i++)
    {
        switch (arr[i].op)
        {
        case Data:
        {
            printf("%d  ", arr[i].data);
            break;
        }
        case Ope:
        {
            if (arr[i].data == '*' || arr[i].data == '/')
            {
                while (StackNum(&s) && (StackTop(&s) == '*' || StackTop(&s) == '/'))
                {
                    printf("%c  ", StackTop(&s));
                    StackPop(&s);
                }
            }
            else
            {
                while (StackNum(&s) && StackTop(&s) != '(')
                {
                        printf("%c  ", StackTop(&s));
                        StackPop(&s);
                }
            }
            StackPush(&s, arr[i].data);
            break;
        }
        case Left:
        {
            StackPush(&s, arr[i].data);
            break;
        }
        case Right:
        {
            while (StackTop(&s) != '(')
            {
                printf("%c  ", StackTop(&s));
                StackPop(&s);
            }
            StackPop(&s);
            break;
        }
        }
    }
    while (StackNum(&s))
    {
        printf("%c  ", StackTop(&s));
        StackPop(&s);
    }
    printf("\n");
}

/////test.c
int main()
{
    cell arr[] = { {Data,12},{Ope,'*'},{Left,'('},{Data,3},
    {Ope,'+'},{Data,4},{Right,')'},{Ope,'-'},{Data,6},{Ope,'+'},
    {Data,8},{Ope,'/'},{Data,2} };
    MidTurnBack(arr, sizeof(arr) / sizeof(arr[0]));
    system("pause");
}

运行结果：

上面代码中栈的基本函数可在

https://blog.csdn.net/qq_39032310/article/details/81950247 (栈的基本操作)中查看。

如果有什么疑问或者更好的提议欢迎留言。