20ZR暑期联赛班 最短路和生成树
欧拉回路
P1341 无序字母对
给定 n n n 个各不相同的无序字母对。请构造一个字典序最小的 有 ( n + 1 ) (n+1) (n+1) 个字母的字符串使得每个字母对都在这个字符串中出现。
给定的字母对两个字母必须连续出现,而且只出现一次。所以考虑将构成无序对的两个字母连无向边,如果构成的图是欧拉图,那么有解跑欧拉回路即可。因为要求字典序最小,所以每次先遍历小点再遍历大点,可以用一个堆维护。
CF547D Mike and Fish
给定平面上的 n n n 个点的坐标,你需要将每一个点进行红蓝. 染色,满足任意一行一列红蓝点的数量之差不超过 2 2 2。 1 ≤ n ≤ 2 × 1 0 5 1 \leq n \leq 2 \times 10^{5} 1≤n≤2×105
先对坐标离散化。对于一个点 ( x , y ) (x,y) (x,y) 我们连一条 x x x 到 n + y n + y n+y 的边,那么问题转换成了给边定向,让每个点的入度和出度之差不超过一。分类一下,度数相同的在无向图上就是每个点的度数为偶数。度数差为一的在无向图上每个点的度数为奇数,那么再把这些奇数点连到虚拟点上,那么度数就是偶数了,再考虑虚拟点,因为奇数点个数一定为偶数,跑欧拉回路即可。
还有二分图染色的方法。将横纵坐标相同的点两两连边,构成了二分图,剩下的点最多一个不用管。然后进行二分图染色即可。女少口阿。
P4568 飞行路线
给定一张 n n n 个点 m m m 条边的带权无向图,你可以把至多 k k k 条边的边权变成 0 0 0,求从 s s s 到 t t t 的最短路。 2 ≤ n ≤ 1 0 4 , 1 ≤ m ≤ 5 × 1 0 4 , 0 ≤ k ≤ 10 2 \leq n \leq 10^{4}, 1 \leq m \leq 5 \times 10^{4}, 0 \leq k \leq 10 2≤n≤104,1≤m≤5×104,0≤k≤10。
分层图。设 d i , j d_{i,j} di,j 为到 i i i 点用了 j j j 次的最短路。
P2761 软件补丁问题
有一款软件有 n n n 个 BUG,还有 m m m 个补丁。 对于每一个补丁,都有两个 BUG 集合 B 1 , B 2 , B_{1}, B_{2}, B1,B2, 表示只有当 这个软件包含了 B 1 B_1 B1 中的所有 BUG 而不包含 B 2 B_2 B2 中的任意一个 BUG 的时候,这个补丁才能使用。
对于每一个补丁,它会修复一个 BUG 集合 F 1 , F_{1}, F1, 同时引人 另一个 BUG 集合 F 2 , F_{2}, F2, 运行需要 t t t 的时间。 求将所有 BUG 都修复需要的最短时间,无法修复输出 − 1 -1 −1。
1 ≤ n ≤ 20 , 1 ≤ m ≤ 100 1 \leq n \leq 20,1 \leq m \leq 100 1≤n≤20,1≤m≤100
将 BUG 状压,把一个状压的状态看成一个点,如果通过一个补丁能从一个点到另一个点,那么就连边,边权为时间。跑 Dijkstra 即可。
生成树 瓶颈树 最短路树
最小生成树即为最小瓶颈树,最大生成树即为最大瓶颈树。
void Kruskal() {
int ans = 0;
for (int i = 1; i <= n; i++) f[i] = i;
sort(e + 1, e + tot + 1, cmp);
int cnt = 0;
for (int i = 1; i <= m; i++) {
int x = e[i].x, y = e[i].y, z = e[i].z;
int ux = find(x), uy = find(y);
if (ux != uy) {
ans += z; f[ux] = uy;
if (++cnt == n - 1) break;
}
}}
如果将一个点到其余所有点的路径保留其它的删掉,那么构成了一棵树,这棵树叫最短路树。
P1967 货车运输
一张 n n n 个点 m m m 条边的图,每一条边有一个限重。 现在有 q q q 组询问,每次问你从 u u u 到 v v v,在不超过限重的情况下,重量最大可以是多少。 n ≤ 1 0 4 , m ≤ 5 × 1 0 4 , q ≤ 3 × 1 0 4 n \leq 10^{4}, m \leq 5 \times 10^{4}, q \leq 3 \times 10^{4} n≤104,m≤5×104,q≤3×104
解法还是很多的,这里可以发现要让最小值尽可能大,所以建立一棵最大生成树。把路径用 lca 转一下即可。
P3953 逛公园
给你一张 n n n 个点 m m m 条边的有向图,问你从 1 1 1 到 n n n 与最短路的 差不超过 k k k 的路径有多少条。 可能有 0 0 0 边,如果数量无限输出 − 1 -1 −1。路径可以重复经过一个点。
n ≤ 100000 , m ≤ 200000 , k ≤ 50 n \leq 100000, m \leq 200000, k \leq 50 n≤100000,m≤200000,k≤50。
可以发现,合法路径有无限个当且仅当有一个全为 0 0 0 的环中的一个点在最短路的路径上。先正反建边跑一下 dijkstra,令 d 1 d_1 d1 为 1 1 1 的单源最短路, d 2 d_2 d2 为 n n n 的单源最短路。对于一条边 ( u , v ) (u,v) (u,v),如果有 d ( u ) + d ( v ) = d n d(u) + d(v) = d_n d(u)+d(v)=dn,这意味着 w ( u , v ) = 0 w(u,v) = 0 w(u,v)=0,那么把这条边加入新的图中。再拓扑排序判断有没有环,搞定了 − 1 -1 −1。
k k k 小,那么就分层图了。设 f i , j f_{i,j} fi,j 为从 1 1 1 到 i i i,与最短路差为 j j j 的路径有多少条。用类似最短路松弛的方式计数转移即可。
CF1163F Indecisive Taxi Fee
3k 难度的神仙题,能学到不少套路。
给你一张 n n n 个点 m m m 条边的图,有 q q q 次询问,每次问你如果更改一条边的边权,从 1 1 1 到 n n n 的最短路是多少。
容易想到正反建边,预处理处理从 1 1 1 和从 n n n 走的最短路径,分别为 d 1 d_1 d1 和 d 2 d_2 d2。分类讨论一下,令改的是 ( a , b ) (a,b) (a,b) 这条边
- 改的边不在最短路上,且改大了。不用管。
- 改的边不在最短路上,且改小了。拿 d 1 ( a ) + d 2 ( b ) + w ( a , b ) d_1(a) + d_2(b) + w(a,b) d1(a)+d2(b)+w(a,b) 与原来的最短路取最小值。
- 改的边在最短路上,且改大了。新的最短路有可能绕过被修改的边,好像不好搞先一放。
- 改的边在最短路上,且改小了。在最短路的基础上减一下即可。
考虑第三类。如果把改的边删掉,求不经过这条边的最短路,与原来的最短路加改边产生的贡献取最小值即可。而且求不经过某条边的最短路会有多次询问。
先考虑经过一个点的最短路,可以删最短路上点的范围。
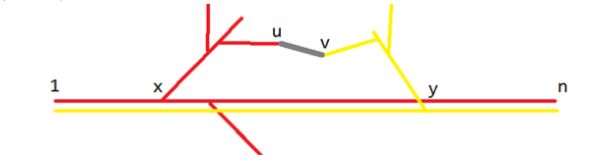
令最短路为 E 1 ∼ E k E_1 \sim E_k E1∼Ek,枚举一条边 ( u , v ) (u,v) (u,v)。经过 ( u , v ) (u,v) (u,v) 的最短路径也会经过 E 1 ∼ E x E_1 \sim E_x E1∼Ex 和 E y ∼ n E_y \sim _n Ey∼n,相当于最短路的前缀和后缀或为空。那么考虑求 x x x 和 y y y,可以在前面的第一次 Dijkstra 中,记录最短路的路径,在正反两向的 Dijkstra 分别求出每个点的 x x x 和 y y y。如果能松弛,看看点在不在最短路径上,不在的话就继承父亲的 x x x 或 y y y,正确性显然。因为最短路先松弛下标小的点,所以不用担心有另一个最短路的范围比我们求的大。
再考虑经过一条边允许删的点的范围,考虑边的两个点 u , v u,v u,v 可能会有多个情况,所以范围是 u x + 1 ∼ v y − 1 u_x + 1 \sim v_y - 1 ux+1∼vy−1 和 v x + 1 ∼ u y − 1 v_x + 1 \sim u_y - 1 vx+1∼uy−1。那么维护一棵 1 ∼ k 1 \sim k 1∼k 的线段树,将这两段用 d 1 ( u ) + d 2 ( v ) d_1(u)+d_2(v) d1(u)+d2(v) 更新最小值即可。查询时,找不包括给定边的两个点的所有区间的最小值。
细节多,时间复杂度 O ( ( m + q ) log n ) O((m+q) \log n) O((m+q)logn)。确认了码量,是我调不出的题 /kk。