最短路径 Dijkstra 算法

最短路径可以说是出名的算法问题了，无论现实中还是数据结构上都十分有意义，两点之间距离最短的走法。基于离散数学图论，对于给定的点级和边集，边的权值模拟距离。在无法确定中转还是直达最快的情况下，通过算法找出最短的距离。

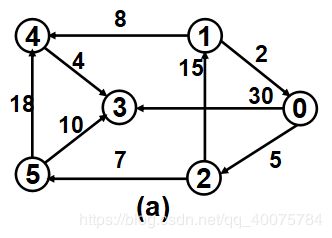
解析

一般而言，Dijkstra 算法适用于单源点（入口）有向边，经过改进可适用于无向边。数据表示需要一种方法，处理则是核心。

数据结构

为了方便描述，所有点以数字或字母表示，以0或a作为入口。
对于边集的表示两种方法：
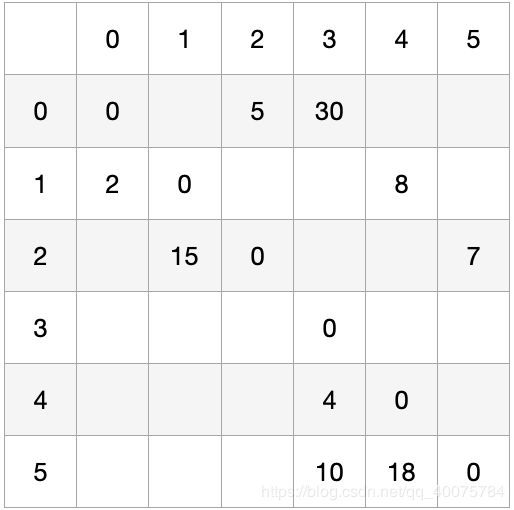
用邻接矩阵，即如果两点间存在边就将权值放在二维数组，其他位置设为无限（以变量上限值标记）。个人觉得表示方法一般，优点是比较清晰。

第二种方法是用三元组表示每条边，格式为【起点，终点，权值】，比如 Py 里的 list、C/C++ 的结构体链表。个人认为边少时比较合适。
另外需要用一个 visit 数组表示每个点是否访问过处理过，一个 via 数组表示两点间是直达还是从哪个点中转更快，下面会提到怎么写。（我重新命名了）
本文使用 Python：用三元组形式表示边，对于无边或不可达用 None 表示，处理上也就复杂一点；dist 数组为源点0到各边距离，当处理完就是最短距离；via 数组是一维的，如果到点i经过i表示直达，否则表示绕路。

输入

输入没什么好说，依次输入起点、终点、距离，找个条件退出输入。一般来说两点间同向边不能重复，必然有一个短一点没意义，输入函数可以用来检查是否重复。

思路

Dijkstra 算法用到了贪婪策略，将点分为已确认和未确认最短路径的两部分，每一轮取最短距离加入已处理集合。
首先将入口（本文是0）到各点距离加入到 dist，标记点0为已访问。然后找离点0最近的点进行下一波操作，最近的点就是确认了最短路径的，比如点2。

这里需要简单的数学证明：离0最近的点没有比直达的更短路径，如果存在中转的更短路径，中转点就是离0最近的而非这个点。比如图中点3不是离0最近，可能存在0-2的中转。对于已确认最短路径的点，可以看作一个整体，到下一个距离最短的点必然是最短路径。
现在以点2为中转点，检查到其它的点是否比原本更近，或者到达了新的点（在本文条件即0不能直达的），找到了 2-5 和 2-1，那么 dist 数组更新对应位置。

然后在未访问的点找最近的（0和2已访问），找到点5作为中转点，然后发现新到达点 5-4，另外 0(-2)-5-3 的距离比 dist 数组（即 0-3）短要修改。

然后是选择点1作为中转，找到 (0-2)-1-4 比当前到 (0-2-)-5-4 短，更新。
然后选择点3，没有可更新的。

这个时候已经是完成了。虽然还有一个点没有访问，但是如果只剩一个点没有访问，其它点都找到最短路并且做过中转，那么剩下一个也是最短路径。单源点可以根据 false 剩余1个作为退出条件，如果强行在 Dijkstra 算法添加双源点，但是设定了源点，那么退出条件就是没法找到可访问的点，从设定的源点到多出来的源点距离 None 即不可达。本文采用后种方法退出。

输出

dist 数组比较简单，从0到各点最短距离就在数组。路径输出稍有难度，按照 via 数组情况举例，via[2] 是2表示0到2直连，举 via[3] 是5为例：到3要绕路经过5，到5要绕路经过2，到2就是直连，所以先输出 0-2，递归返回后输出 -5，然后递归返回输出 -3，结束。

Python 代码

这段代码稍微说下：因为懒得一条条边输入，没启用 inPath 函数，这个是用来输入一条边并且统计节点的；dijkstra 函数输入边的集合和点的数量，因为 None 不能和 int 比较，所以要先处理 None 的情况；view 函数直接放在处理好结束，findPath 函数通过递归找最短路径经过的点.

def dijkstra(path, amount):
    dist = [None]*amount
    via = [None]*amount
    # visit 记录是否检查过
    visit = [False]*amount
    # 先将点0到各点最短距离加入
    dist[0] = 0
    visit[0] = True
    via[0] = 0
    for r in path:
        if r[0] == 0:
            dist[r[1]] = r[2]
            via[r[1]] = r[1]
    while visit.count(False) != 0:
        mini = None
        # 从未确认的点中找出最近的
        for i in range(len(dist)):
            if not visit[i] and dist[i] is not None and (mini is None or dist[i] < dist[mini]):
                mini = i
        if mini is None:
            break
        visit[mini] = True
        for p in path:
            # 如果从这个点中转比直连快，或者只能中转到达
            if p[0] == mini and (dist[p[1]] is None or dist[p[1]] > dist[mini] + p[2] ):
                via[p[1]] = mini
                dist[p[1]] = dist[mini] + p[2]
    view(dist, via)


def in_path(path, node):
    start, end, value = (int(input()), int(input()), int(input()))
    # 检查是否重复
    for r in path:
        if r[0] == start and r[1] == end:
            return
        # 对于新加入点记录
        if node.count(r[0]) == 0:
            node.append(r[0])
        if node.count(r[1]) == 0:
            node.append(r[1])
    path.append([start, end, value])


def view(dist, via):
    for i, d in zip(range(len(dist)), dist):
        print("from %d to %d:" % (0, i), d, end=", ")
        print("0", end="")
        findPath(via, i)
        print()


def findPath(via, i):
    if via[i] != i:
        findPath(via, via[i])
    print("-", i, sep="", end="")


# data struct of path [start, end, value]
path = [[0, 2, 5], [0, 3, 30], [1, 0, 2], [1, 4, 8], [2, 1, 15], [2, 5, 7], [4, 3, 4], [5, 3, 10], [5, 4, 18]]
node = []
# in_path(path, node)
# dijkstra(path, len(node)
dijkstra(path, 6)