排序大冒险(更新呢!)
前言
要活动更好的阅读体验,戳我
最近,我美化了我的blog.但是文章很少,为了避免华而不实 (就是因为我懒) ,我决定从今天开始更文啦~
(安利一个链接)
OI知识树
排序源代码下载
想用迅雷下载?
https://crab-in-the-northeast.github.io/downloads/all_sorts_code.zip
声明:本篇文章为东北小蟹蟹原创,部分图片从百度百科搬来。转载不用跟我说,但请附上原文地址。
阅读本文你需要:
1.有一个对编程良好的态度
2.对事物有好奇心
3.会C++基础语法
背景
前半部分背景戳这里
三年之后……
突然,一个螃蟹找到了我。
他自称他叫“小排”,然后领我带到了一个隧道,
有一个紧锁的门。门上写着:
1,4,5,6,8,2,8.
上面有一个牌子,写着“谁要是通过了这个隧道,就可以获得无价之宝”。
右边是一台迷你计算机,左面的墙壁写了一个很大的"sort".
我顿时明白了,原来是让我们编辑代码来把数字排序啊!
门上还刻有一行英文:
You can't use the same kinds of sorts in two or more levels.
(每一关都要用不同种类的排序)
于是,我便和小伙伴踏上了冒险之路。。。。
(ps:不要管螃蟹是怎么打字的)
冒险开始了!
基于数值的排序 number
计数排序 counting sort
概念 conception
“这怎么办?” 小排抱怨。
我沉默不语,在沙滩下画上了8个格子。
小排好奇地瞅着我,问道:“这是什么意思呀?”
“你看,牌子上的数组是1,4,5,6,8,2,8吧。”
“嗯嗯。”
“这些格子的初始值都是0哈,首先来访的是1,所以我把第一个格子的数值+1.”
“嗯。这个时候8个格子分别为1,0,0,0,0,0,0,0了。”
“然后又来了4,所以我们把第四个……”
他迫不及待地把第四个格子里填了1.看来他还是挺聪明的。
他也不把用来写字的树枝还给我。不过我很开心,因为他明白了。
“可是到达第7个数,8已经是1了,怎么搞?”
“那你就再+1呗。”
于是,格子里的数字分别是
“1,1,0,1,1,1,0,2”
“所以你到底要干甚?”
“你想想看~”
他深思熟虑了片刻。你也思考思考吧~答案请往下翻。
|
|
|
S
l
i
d
e
d
o
w
n
t
o
s
e
e
n
e
x
t
p
a
g
e
!
|
|
|
他顿时大雾悟,明白了OI能让人掉多少头发。
“我们只要从第一个格子开始遍历,然后输出这个格子所对应的值次的下标,就可以排序了!”
“bingo!这就是计数排序,完美~”
这里我再解释一下:
现在我们有了8个格子。
刚才说过格子里的数字分别是
“1,1,0,1,1,1,0,2”
第一个,值是1,下标是1,所以输出1次1,输出了1
第二个,值是1,下标是2,所以输出1次2,输出了2
第三个,值是0,下标是3,不输出
第四个,值是1,下标是4,所以输出1次4,输出了4
第五个,值是1,下标是5,所以输出1次5,输出了5
第六个,值是1,下标是6,所以输出1次6,输出了6
第七个,值是0,下标是7,不输出
第八个,值是2,下标是8,所以输出2次8,输出了8 8
尤其是 第八个 要格外小心。
所以输出了1 2 4 5 6 8 8.
哇,这是我们学习的第一个排序算法,干杯~
代码 code
代码就很显然了,如下:
#include 练习 practicing
再实现一次倒序。
提示:很简单,倒着遍历就行了~
分析 analysis
这个算法的正确性毋庸置疑,那么复杂度呢?
我们设k为数组中的最大值。
时间复杂度 是O(n+k),时间复杂度较低。
空间复杂度 也是O(k),那么这是优点还是缺点?留个悬念,一会讲。
果然,小排知道了计数排序的优点之后,就觉得计数排序无敌了!
计数排序是很好,因为 时间复杂度 很低。
但是没有任意一个算法是无敌的,OI算法的水深,他不被淹是不知道的。
所以,我考验他一下,
还是排序。数列变成了这样:
-2122,9.990,2147483646,13131314,123456789,-123123123
真是极品数据233
果然他又哭着找我了,说我欺负它。
原因嘛你懂得,不懂你模拟一下就有bug了。
顺便说一下,这个排序算法是稳定排序。
“东北小蟹蟹,什么是稳定排序啊?”
“如果原数列有两个值是一样的,并且排序后,这两个值的相邻关系一定不变,就是一开始排序的两个等值谁在前谁在后,排序后一定还是那个在前的在前,在后的在后,那么这个排序就是稳定排序,如果不能保证这个关系,则是不稳定排序。由于,你把数扔进对应的格子里,计数器+1,则从前往后遍历,一定顺序不变。所以,这个排序是稳定排序。并且我们要注意不稳定指的是未知,有可能还是原来的顺序,但是有可能就不是。不懂这个也没有关系,重要的是思维。”
啰嗦了这么多,现在我们来总结一下计数排序:
计数排序的优点:
时间复杂度低。
计数排序的缺点:
对数据要求比较高。
哦,对了,就算数组不会爆炸,特大的数据会导致时间复杂度中O(n+k)都会炸。
基数排序 radix sort
概念 conception
大门打开了~
我们来到了第2关。
数列是这样的:
123,98,141,313,344
小排刚一萌生起用计数排序的想法,就见到门上霎时出现了一行英文:
No counting sort! Don't use any algorithms about comparing!
哎?这门难道有灵异功能?不管了233…
门上告诉我们“不能用基于比较的排序和计数排序!”
那么……
“小排,你过来看。” 我把小排叫过来。
“嗯嗯。东北小蟹蟹,你又有啥思路了?”
“这个和计数排序差不多。首先我们定义10个格子,为了更形象一点,我们说成‘桶’。”
“然后你看见这几个数了吧,我们按个位把它丢进相应的桶。”
“什么玩意儿???”
“你看,第一个来的是123,个位是3,所以我们把它丢进3号桶。”
“哦哦!那其他的照样丢呗~”
“对滴!丢完后变成这样:”
0号桶:空
1号桶:141
2号桶:空
3号桶:123,313(按顺序丢)
4号桶:344
5号桶:空
6号桶:空
7号桶:空
8号桶:98
9号桶:空
“好了,我们再按照计数排序的思路依次取出这些数。”
“这个数列就变成了:141,123,313,344,98.”
“对对!个位已经排好序了。”小排机敏地回应。
“所以再按照刚才的思路排十位。”
“我来吧我来吧!”他又抢过了树枝。
0号桶:空
1号桶:313
2号桶:123
3号桶:空
4号桶:144,344
5号桶:空
6号桶:空
7号桶:空
8号桶:空
9号桶:98.
“再依次取出。”
313,123,144,344,98.
“接下来我全都知道了!!!”小排兴奋地大叫。
“再把百位排一遍。”
这该怎么排?请你自己试一试吧~
(ps:98的百位是0)
|
|
|
S
l
i
d
e
d
o
w
n
t
o
s
e
e
n
e
x
t
p
a
g
e
!
|
|
|
如果你算得没错,答案应该是:
98,123,144,313,344.
“哎?这怎么就变有序了?”
“嗯。这个排序就叫做基数排序。也是很好用滴。”
刚才提到了桶,顺便提一下,其实桶排序,基数排序和计数排序都是差不多的,但也有区别,一会我们会讲的~
并且,刚才所讲的基数排序,使用的是LSD (Least Significant Digit first) 是从低位到高位分配。
还有一个MSD (Most Significant Digit first) 是从高位到低位分配。这比LSD要麻烦许多,这里就不再赘述了。
代码 code
这个代码比计数排序要难得多,其中用了STL.
没有看懂的可以直接跳过这里,这个代码不重要。
重要的是思路和原理。
#include
#include
using namespace std;
int getlen(int n)//获取一个数的长度
{
int ret=0;
while(n)
{
n/=10;//n不断除以10
ret++;
}
return ret;
}
vector bucket[10];//用了STL
int n,a[10],tmp[10],maxlen,bk,divpos=1;
//有n个数,第i个数是a[i],tmp是临时数组
//maxlen是数组中最大数的长度,bk是数组下标的遍历
//divpos用来变化求一个数的每一位
int main()
{
cin>>n;
for(int i=0;i>a[i];
maxlen=max(maxlen,getlen(a[i]));
}
//以上都是读入
while(maxlen--)
{
for(int i=0;i<10;i++)
bucket[i].clear();//初始化
for(int i=0;i::iterator iter=bucket[i].begin();
for(;iter!=bucket[i].end();iter++)
tmp[bk++]=(*iter);
//用iterator遍历,把这些数再重新取出
}
bk=0;//初始化下标遍历变量bk
for(int i=0;i 练习 practicing
排序:第一行为数据个数,第二行为数据。
输入:
9
999 1083 4194 5141 5341 4654 4245 1312 3543
输出:
999 1083 1312 3543 4194 4245 4654 5141 5341
或者将基数排序提交到这里。
分析 analysis
先看一下如何证明基数排序。
假设所有数的位数都一样……
小排大叫:“假设?那如果不一样呢?”
“不一样就补0呗,补到所有数的位数一样为止,也不能补多,所有数的最高位不能全是0”
好,我们继续证。
如果所有最高位……小排你别冲动,如果所有最高位都不相同……小排!别皮了!
那么,肯定最高位数小的整个数就小。所以最后排完百位之后如果百位都不相等,排序自然就ok了。
当然最高位有可能是相同的,小排你爽了吧~所以我们之前要比后面的几位,原理嘛很简单。
把后面的几位分别想象成最高位,然后再带回刚才的证明思路就行了。
正确性证明完了,但是相信你看到上面那些代码后一定有骂人的冲动。为什么?太麻烦了。
这就是其中的一个缺点。
而且,这还是无法解决负数和小数的问题。这还是一个缺点。
但是解决了计数排序中最大值过大的问题。这是优点。
并且时间复杂度为 O(d(n+k)) .
其中n表示有多少个数,d表示待排序列的最大位数,k表示每一位数的范围(在正常的数中范围自然是10.)。
因为用了STL,所以空间复杂度求解比较困难。不过一般不会炸。
现在来总结一下基数排序吧~
基数排序的优点:
1.解决了计数排序留下的空间爆炸问题。
2.时间复杂度降低了不少。
缺点:
1.代码比计数排序难懂并且复杂。
2.还是无法解决小数与负数的问题,对数的要求仍然很高。
需要注意的是,这种排序属于 稳定排序
并且其中的位值原理是非常重要的一部分,大家需要了解。
因为时间复杂度的原因,这个排序经常用来卡常数。
好了,第2关也过了,好开心~~~
桶排序 bucket sort
趁小排去上厕所了,悄悄给你们科普一下桶排序。
(别问我为什么)
相信经过上面几轮关于计数的排序的洗礼后,一定对这种套路有所了解了。
这里简单介绍一下桶排。
假设说我有一个序列,每个数的取值范围都是1-1000
然后再来若干个桶,比如第一个桶存1-10的数,第二个桶存11-20的数。。。
很显然就有100个桶了。
当然第一个桶存1-100也无所谓,这样就是10个桶。
然后分别把这几个桶用其他的排序,比如刚刚学到的计数和基数
以及下面要学到的冒泡排序,选择排序,快速排序,希尔排序,等等等等。
然后再把这些桶合在一起就ok了。
假设一共有n个数,m个桶,最大值是k.
如果可以恰好把n个数平均分给m个桶,并且对每个桶使用 快速排序
时间复杂度 是
O(n+m*n/m*log(n/m)+k)=O(n+nlog(n)-nlog(m)+k).
可见n接近于m话,时间复杂度是O(n+k).
其实我们会发现如果n=m,这就是一个现成的 计数排序 了。
但事实上这是最好情况,在最坏情况m=1的情况下,就和一般的排序没啥区别了。
既然桶最多是最好情况,为何不用计数排序?
原因很简单,计数排序把把所有的空间都开销了,很多空间根本就没有使用。
而桶排序是一段一段的,能减少空间浪费率。
也就是减少 空间复杂度
虽然浪费了点时间,但是节省了大量空间,这是十分划算的。
优缺点也很显然了。见“计数排序”。
还有两个缺点:排序是 不稳定排序 ,代码麻烦。
所以桶排序也比较罕见。
基于计数的排序,比较常用的,也就是计数排序了。
基于比较的排序 comparing
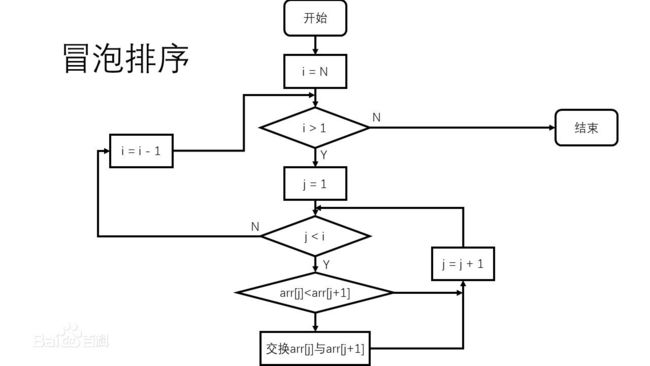
冒泡排序 bubble sort
概念 conception
小排上完厕所回来了。我们来到了第3关。
第3关是这样的:-3333,1.131,19191919191919199119191,2314513.333,-1.13415726
由于数据很极端,满足不了 傲娇的基于计数的排序们了。
气得小排一直在那里画圈。嘴里还咕哝什么。
我思考了片刻……
“小排啊,别抱怨了,我有一个思路了。”
他赶紧过来瞅瞅我有什么新进展。
“你看,从小到大排序,那么是不是大的在最后啊~”
“嗯嗯,这不废话么”
“但是这句话对我接下来要讲的 异常关键 ”
“我们可以从第一个数开始,如果第一个数>第二个数,也就是”
“a[i]>a[i+1]”
“不符合规则,我们就可以”
“swap(a[i],a[i+1])”
“swap就是交换的意思。”
“拿一个例子举例一下。 这关的数列太毒瘤就不拿这个了 ”
“5,3,2,4,1.”
“好了,从第一次开始:”
“5和3比较,发现 满足a[i]>a[i+1],将5,3交换。”
“3,5,2,4,1.”
“第二次,再看第二个和第三个:”
“ 5>2.发现满足a[i]>a[i+1],将5,2交换。”
“3,2,5,4,1”
“然后就这么变 ^ _ ^”
“3,2,4,5,1”
“3,2,4,1,5.”
“OK,是不是发现第一大的数已经归位了?”
“像不像一个数泡泡不断地根据规则往上浮?”
“所以这个排序也叫冒泡排序。”
“我们把刚才的那些交换操作统称为‘一趟’。”
“接下来的几趟规则都是一样的。小排,到你了。”
“啊?到我了是么?”
“2,3,4,1,5”
“哎呀,3和4并不满足a[i]>a[i+1],不交换会不会对后面有影响啊?”
“不会的你放心吧。”我回答。
“2,3,1,4,5”
“哇好神奇!!!第二大的也归位了!!”
“嗯嗯!然后再遍历几趟~”
“哎,说太麻烦了……”
他拿来了刚才画圈的那只树枝,写下了:
2,1,3,4,5
“1和3不满足a[i]>a[i+1],不交换。”
“这又是一趟~”
1,2,3,4,5
“嗯姆??竟然真的排序成功了!”
“嗯。你现在已经懂了冒泡排序的精髓了。”
“冒泡排序的精髓是:每次比较相邻的两个元素,如果他们的顺序错误就把他们交换过来。”
代码 code
冒泡排序也是比较简单的~
#include 练习 practicing
1.基础:
输入:
10
8 100 50 22 15 6 1 1000 999 0
输出:
0 1 6 8 15 22 50 100 999 1000
2.挑战:
输入几名同学的名字和分数,按分数从小到大排序输出名字。
(1) 使用结构体
(2) 不使用结构体
输入:
5
kkksc03 100
noip 21
chen_zhe 99
0x7fffffff 33
me 0
输出:
me
noip
0x7ffffff
chen_zhe
kkksc03
当两人成绩相同,爱咋输出咋输出。
注:本题标程在开头的源文件中有
有结构体版本请查看bubble_sort_prac_use_struct.cpp
无结构体版本请查看bubble_sort_prac_unuse_struct.cpp
分析 analysis
冒泡排序的正确性不难证明。
冒泡排序的核心代码是双重嵌套循环,不难看出时间复杂度是O(n^2).
这在排序中可谓是一个十分高的复杂度了。
在发现冒泡排序后有许多dalao尝试对冒泡排序改进,但都没有成功。
Donald E. Knuth(高德纳,1974图灵奖获得者)曾说过:
冒泡排序除了它迷人的名字和导致了某些有趣的理论问题这一事实之外,似乎没有什么值得推荐的。
好啦,总结时间到了。
冒泡排序的优点:
对数据要求不大,不苛刻。
缺点:
时间复杂度很高。
高德纳dalao都发话了,那肯定有值得推荐的算法啊,还愣什么?Go!Go!Go!
选择排序 selection sort
直接选择排序 straight selection sort
概念 conception
第4关的大门也向我们开启了。
这次可谓是直截了当,门上没有显示数列,仅刻有一行英文:
Use selection sort.
让我们干啥就干啥,我们没得选。纯模拟
“小排,你看。”
“好啦,我过来了。”
“你看,这里有一个数列。2,1,3,5,4.”
“然后呢?”
“我们可以直截了当的想,是不是可以遍历到一个数后,求这个数排序后的下标,让它去他应有的地方就行了?”
“对啊,关键是你怎么求下标。”
他深思熟虑了片刻。。。。
你也想想看,能不能想出来怎么求下标呢?
|
|
|
S
l
i
d
e
d
o
w
n
t
o
s
e
e
n
e
x
t
p
a
g
e
!
|
|
|
“我们可以每到一个数,将其和后面的数列中求出最小值,将这个最小值和他交换就行了。” 小排说道。
“妙哉,汝秀也!”
“现在我们用刚才说的那个例子来看。”
2,1,3,5,4
“首先我们的可爱的循环变量i到了第一个数2.”
“此时可爱的j向后望去,到了第二个数1.”
“发现a[i]>a[j],swap(a[i],a[j]).”
“swap是什么意思啊?” 小排突然插了一句嘴。
“刚才说啦,是交换的意思。你又没认真听讲。”
“我们继续,j向后继续遍历,发现没有比他小的了。”
此时,数列变成了:
1,2,3,5,4.
“然后我们可爱的小i来到了第二个数2.”
“后面没有比2还要小的了,所以i++,来到3...”
就一直这么下去,最后我们会发现数列变成了:
1,2,3,4,5.
“妙哉,妙哉!”小排大叫。
好了,直接选择排序我们就讲完啦~
真是够狠,够直接,看看这排序的英文名你就知道了。
代码 code
直接选择排序也很简单的~
#include 练习 practicing
排序:
5
5 3 4 2 1
1 2 3 4 5
自己敲一遍code
分析 analysis
分析?瞎分析
好吧我们还是正经的分一下析
这个排序的证明嘛,首先引用小排的一句名言:
我们可以每到一个数,将其和后面的数列中求出最小值,将这个最小值和他交换就行了。
这是名言?
这就是直接选择排序的精髓。
证明方法很简单:
假设我们来到了第一个数,然后向后寻找最小值:
如果找到了,替换了,第一个数就是全数列的最小值。
如果没找到,说明第一个数就是全数列的最小值。
反正第一个数搞完后肯定是最小值
然后我们又来到了第二个数,这时最小值已经是第一个了。
所以再往后找的最小值就是第二小的。
经过这么一趟折腾,第i个数就是第i小的数。
自然我们就完成了排序的目的。
正确性证明完了,现在来看看把数万考生折磨的生不如死的复杂度:
时间复杂度:双重嵌套循环,O(n^2)
空间复杂度:O(n).
其实后面排序的空间复杂度基本上都是O(n).
哎,可惜的是这玩意儿复杂度还是很高。
带着悲痛的心情总结一下直接选择排序:
直接选择排序的优点:
一样,对数没有特殊要求
缺点:
慢,比较次数多
不过,这关还是过了,乐观一点把。
堆排序 heap sort
概念 conception
第4关过去了,我们强颜欢笑地到了第5关。
出乎意料的是,门上竟然又出现了Selection sort!
可是,我明明记得……
刚进入隧道时……
门上还刻有一行英文:
You can't use the same kinds of sorts in two or more levels.
(每一关都要用不同种类的排序)
不管了!233,我们仍然用了直接选择排序,但是门并没有开……
我恍然大悟,堆排序也是选择排序啊,应该用的是他。
说起堆排序,我们就得提到一个概念:堆。
“堆是什么鬼?”小排问道。
“堆就是一棵顺序存储的完全二叉树。完全二叉树是什么我之后会写一篇文章讲到。”
“没事,我知道。”
“嗯。堆又分为大顶堆和小顶堆。”
这里放一张图:
(注:此图来源于这里,感谢作者提供此图。接下来所有堆的静态图片都出自于此。)
“嗯,我猜你已经想到了。大顶堆的所有根节点的关键字都大于等于其两个子节点关键字。小顶堆则反之。”
把它映射到数组里就是这样:
“这个数组就代表了上上图中的大顶堆。”
“哇哦。”
“你试试用简洁明了的公式来形容一下:”
小排拿过树枝,写下了:
arr[i]>=arr[i*2+1]&&arr[i]>=arr[i*2+2].
“那小顶堆呢?
小排又写下了
arr[i]<=arr[i*2+1]&&arr[i]<=arr[i*2+2].
“好啦,基础知识咱们了解完了,接下来看堆排序是怎么操作的吧~”
Step 1. 构造初始堆(将无序序列晋级为堆)
“先注意一下,如果我们是升序排列就采用大顶堆,反之,降序排列就是小顶堆。由于我们这里用的是升序排列,所以我们采用大顶堆。”
“那么怎么构造呢?”
“假设这是初始序列,我们要把它晋级为堆。”
“我们从最后一个非叶子结点开始。为什么不是叶子节点?他都没有子节点了还调整个啥,浪费表情。”
“最后一个非叶子节点,为了表述方便,我说成‘第一个非叶子节点’。那么这个点找一下,应该是6.”
“现在开始调整,刚才说过大顶堆的定义是:”
arr[i]>=arr[i*2+1]&&arr[i]>=arr[i*2+2].
“也就是根大于等于子节点才行。这棵以6为根的小树就不满足了。如果要调整,则我们跟子节点较大的那个交换,那样一定可以成功。ok,交换完后变成了这样:”
“继续看第二个非叶子节点。对啦,就是0号根节点4.
由于9>8,根节点选择和9交换。嗯,就变成了这样:”
“然后我们会惊喜地发现第一步调整好的小树又混乱了。强颜欢笑.jpg”
“那咋办呀?”小排焦急地说。
“没事,再操作一次呗。”
“于是这个序列变成了这样:”
“到此,我们可爱的无序序列终于晋级成了堆。”
“但别急,这仅仅是step 1.”
Step 2. 将堆顶元素与末尾元素进行交换使末尾元素最大。然后继续调整堆,反复进行交换、重建、交换。(每次都可以得到当前最大的元素)
“按步骤来。”
“首先将堆顶元素9和末尾元素4交换,然后把元素9剪掉。”
“好的,我们成功取到了最大值。”
“再重复进行Step 1重建。”
“重建完毕,继续取最大值,将其和末尾元素交换。”
“然后又双叒叕重建。”
“好了,我帮你把前两大的剪完了,剩下的轮到你了。”
|
|
|
S
l
i
d
e
d
o
w
n
t
o
s
e
e
n
e
x
t
p
a
g
e
!
|
|
|
“如果你模拟的没有错,最终结果应该是这样的:”
“至此我们完成了排序。”
小排都快睡着了,这排序算法到底有何优点?
请听下回分解。
(注:此图并不是上述作者所作)
代码 code
抱歉并不是这回分解,是下回。
上代码咯,请慢慢享用。
#include 练习 practicing
1.尝试用小根堆实现一下倒序
(源代码里面有,名字是heap_sort_prac_