语音识别—声学模型解码

                                                                    声学模型解码（带状态转移概率）

  最近一直在学习哥伦比亚大学与爱丁堡大学语音识别课程，并且修正了哥伦比亚大学中基于HMM构建的语音识别系统存在问题终自己写了一套基于HMM的语音识别系统，前文一些博客简单对上述工程实现以及理论进行了介绍，但是前文进行Viterbi解码时并未融入状态转移概率，虽然转移概率相较于发射概率对于解码结果影响较小，虽然影响较小，但是笔者认为一个优秀的转移概率模型可能对最后的解码结果有一定的影响，现开始对转移概率进行介绍。

一 未融入转移概率解码模型

1.1 状态图

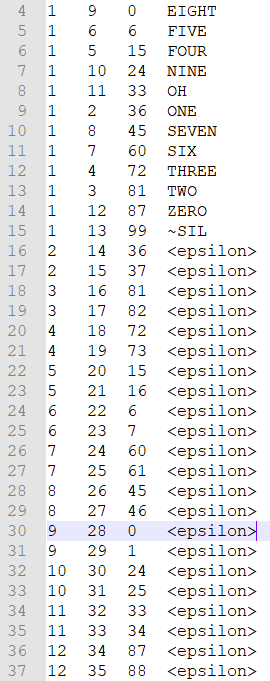
  首先介绍未融入状态转移时的状态图，其图如下所示：

  其中上述状态图中第一至第四列分别表示初始状态、终止状态、GMM状态、词，其中并未涉及状态转移概率

1.2 解码工程化
 

double logProb = (fieldList.size() > 4) ?
  lexical_cast(fieldList[4]) * logFactor : 0.0;

  上述表示未融入状态转移概率的对应帧概率计算方法，默认值为0.

二 融入转移概率解码模型

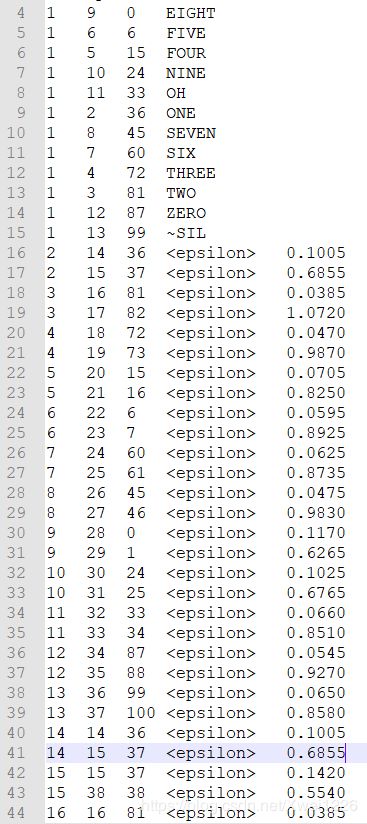
2.1 状态图

  该图中第五列即表示由初始状态转移至终止状态且其对应GMM状态的转移概率，笔者认为转移概率一定程度上会影响基于Viterbi的解码结果。

2.2 解码工程化

double logProb = (fieldList.size() > 4) ?
  lexical_cast(fieldList[4]) * logFactor : 0.0;

  上述表示状态转移概率计算方法，实际应用过程中结合声学模型结果，其具体实现结果如下：

double viterbi(const Graph& graph, const matrix& gmmProbs,
    matrix& chart, vector& outLabelList,
    double acousWgt, bool doAlign) {
    //frmCnt=68, stateCnt=123
    int frmCnt = chart.size1() - 1;
    int stateCnt = chart.size2();
    {
        //计算弧上概率:
        for (size_t frmIdx = 0; frmIdx < chart.size1(); ++frmIdx) {
            for (size_t stateIdx = 0; stateIdx < chart.size2(); ++stateIdx) {
                chart(frmIdx, stateIdx).assign(g_zeroLogProb, -1);
            }
        }
        int startState = graph.get_start_state();
        chart(0, startState).assign(0, -1);
    }

    int frmIdx = 1;
    //当startState=1时，arcCnt=12，arcId=0;
    //arcCnt表示当前状态个数，arcId表示状态在弧上的序号；
    auto startState = graph.get_start_state();
    int arcCnt = graph.get_arc_count(startState);
    int arcId = graph.get_first_arc_id(startState);

    for (int arcIdx = 0; arcIdx < arcCnt; ++arcIdx) {
        Arc arc;
        int curArcId = arcId;
        //arcId表示当前状态按其数目进行从1排序， dstState表示状态排序对应的终止状态；
        arcId = graph.get_arc(arcId, arc);        
        int dstState = arc.get_dst_state();
        double transition_prob = arc.get_log_prob();
        //log_prob表示转移概率加上对应GMM发射概率；
        double log_prob =
            transition_prob + gmmProbs(frmIdx - 1, arc.get_gmm());
        //最后加上弧上chart[0， 1]概率，其值为0；
        log_prob += chart(frmIdx - 1, startState).get_log_prob();
        //针对状态1，将转移概率已发射概率的log概率之和赋值到对应的chart矩阵中；
        chart(frmIdx, dstState).assign(log_prob, curArcId);
        //chart(frmIdx, dstState).printArcResults();
    }

    for (int frmIdx = 2; frmIdx <= frmCnt; ++frmIdx) {
        for (int stateIdx = 0; stateIdx < stateCnt; ++stateIdx) {
            int arcCnt = graph.get_arc_count(stateIdx);
            int arcId = graph.get_first_arc_id(stateIdx);
            for (int arcIdx = 0; arcIdx < arcCnt; ++arcIdx) {
                Arc arc;
                int curArcId = arcId;
                arcId = graph.get_arc(arcId, arc);
                int dstState = arc.get_dst_state();
                double transition_prob = arc.get_log_prob();
                double log_prob =
                    chart(frmIdx - 1, stateIdx).get_log_prob() +  // 表示弧上概率；
                    transition_prob +                             // 表示转移概率；
                    gmmProbs(frmIdx - 1, arc.get_gmm());          // 表示发射概率；
                //如果累加概率log值变小，则替换chart矩阵中对应的状态概率;
                //表示从第一帧开始记录弧序号及其对应的累加概率;
                //当到达最后一帧，chart矩阵中记录着最大概率及其对应的弧序号，可以通过通过回溯得到概率最大的序列；
                if (log_prob > chart(frmIdx, dstState).get_log_prob()) {
                    chart(frmIdx, dstState).assign(log_prob, curArcId);
                }
            }
        }
    }
     
    //chart 矩阵维度为 69*123；
    //其中行表示帧数，列表示累加log似然值；
    //每帧每个位置表示可跳转状态到达此状态时的最大概率；
    //chart 存放结果保存形式为：弧序号(可映射为状态值) 以及 最大似然值；
    //for (int i = 0; i < 123; i++) {
    //    Arc arc;
    //    chart(68, i).printArcResults();
    //}

    return viterbi_backtrace(graph, chart, outLabelList, doAlign);
}

  最后回溯方法得到每个时刻每帧状态似然概率最大位置，并返回弧号以及对应似然值，其具体结果如下：

double viterbi_backtrace(const Graph& graph, matrix& chart,
    vector& outLabelList, bool doAlign) {
    int frmCnt = chart.size1() - 1;
    int stateCnt = chart.size2();
    //finalStates存储终止状态对应的序号，且对其进行排序；
    vector finalStates;
    int finalCnt = graph.get_final_state_list(finalStates);   
    double bestLogProb = g_zeroLogProb;
    int bestFinalState = -1;
    for (int finalIdx = 0; finalIdx < finalCnt; ++finalIdx) {
        int stateIdx = finalStates[finalIdx];
        if (chart(frmCnt, stateIdx).get_log_prob() == g_zeroLogProb) continue;
        //curLogProb表示终止状态对应的似然值与弧上概率的累加值；
        //加上弧上概率是因为终止状态再进行log似然值累加时，终止状态上并未添加弧上概率；
        double curLogProb = chart(frmCnt, stateIdx).get_log_prob() +
            graph.get_final_log_prob(stateIdx);
        if (curLogProb > bestLogProb)
            bestLogProb = curLogProb, bestFinalState = stateIdx;
    }
    if (bestFinalState < 0) throw runtime_error("No complete paths found.");
    outLabelList.clear();
    int stateIdx = bestFinalState;
    for (int frmIdx = frmCnt; --frmIdx >= 0;) {
        assert((stateIdx >= 0) && (stateIdx < stateCnt));
        int arcId = chart(frmIdx + 1, stateIdx).get_arc_id();
        Arc arc;
        graph.get_arc(arcId, arc);
        assert((int)arc.get_dst_state() == stateIdx);
        if (doAlign) {
            throw runtime_error("Expect all arcs to have GMM.");
            outLabelList.push_back(arc.get_gmm());
        }
        else if (arc.get_word() > 0) {
            outLabelList.push_back(arc.get_word());
        }
        stateIdx = graph.get_src_state(arcId);
    }
    if (stateIdx != graph.get_start_state())
        throw runtime_error("Backtrace does not end at start state.");
    reverse(outLabelList.begin(), outLabelList.end());
    return bestLogProb;
}

至此，融入状态转移概率的Viterbi解码方法撰写完毕。