NLP面试知识点整理(一):Word2vec
目录
- 1. NLP的主要研究方向
- 2. Word vectors
- 2.1 离散表示
- 2.2 分布式表示
- Neural Network Language model
- SVD Based Methods
- Word2vec - Iteration Based Methods
1. NLP的主要研究方向
-
信息抽取:从给定文本中抽取重要的信息,比如时间、地点、人物、事件、原因、结果、数字、日期、货币、专有名词等等。通俗说来,就是要了解谁在什么时候、什么原因、对谁、做了什么事、有什么结果。
Information extraction: Extract important information from a given text, such as time, place, person, event, cause, result, number, date, currency, proper noun, etc. In layman’s terms, it is to understand who was at what time, for what reason, to whom, what was done, and what was the result.
< !–对应的英文描述,过了北大复试线就继续英文转换,没过就不用了–> -
信息过滤:通过计算机系统自动识别和过滤符合特定条件的文档信息。通常指网络有害信息的自动识别和过滤,主要用于信息安全和防护,网络内容管理等。
-
舆情分析:是指收集和处理海量信息,自动化地对网络舆情进行分析,以实现及时应对网络舆情的目的。
-
信息检索:对大规模的文档进行索引。可简单对文档中的词汇,赋之以不同的权重来建立索引,也可建立更加深层的索引。在查询的时候,对输入的查询表达式比如一个检索词或者一个句子进行分析,然后在索引里面查找匹配的候选文档,再根据一个排序机制把候选文档排序,最后输出排序得分最高的文档。
-
文本挖掘:包括文本聚类、分类、情感分析以及对挖掘的信息和知识的可视化、交互式的表达界面。目前主流的技术都是基于统计机器学习的。
-
文本生成:机器像人一样使用自然语言进行表达和写作。依据输入的不同,文本生成技术主要包括数据到文本生成和文本到文本生成。数据到文本生成是指将包含键值对的数据转化为自然语言文本;文本到文本生成对输入文本进行转化和处理从而产生新的文本。
Text generation: Machines use natural language to express and write like humans.
-
问答系统:对一个自然语言表达的问题,由问答系统给出一个精准的答案。需要对自然语言查询语句进行某种程度的语义分析,包括实体链接、关系识别,形成逻辑表达式,然后到知识库中查找可能的候选答案并通过一个排序机制找出最佳的答案。
Question answering system: The question and answer system gives a precise answer to a question expressed in natural language. Some degree of semantic(adj. 语义的;语义学的) analysis is required for natural language query(n/v. 疑问,质问;) sentences, including entity links and relationship recognition, to form logical expressions, and then to find possible candidate answers in the knowledge base and find the best answer through a sorting mechanism.
-
对话系统:系统通过一系列的对话,跟用户进行聊天、回答、完成某一项任务。涉及到用户意图理解、通用聊天引擎、问答引擎、对话管理等技术。此外,为了体现上下文相关,要具备多轮对话能力。
Dialogue system: The system uses a series of dialogues to chat, answer, and complete a certain task with the user. It involves technologies such as user intention understanding, general chat engine, question answering engine, and dialogue management. In addition, in order to reflect the context, it is necessary to have multiple rounds of dialogue.
-
语音识别和生成:语音识别是将输入计算机的语音符号识别转换成书面语表示。语音生成又称文语转换、语音合成,它是指将书面文本自动转换成对应的语音表征。
-
机器翻译:把输入的源语言文本通过自动翻译获得另外一种语言的文本。机器翻译从最早的基于规则的方法到二十年前的基于统计的方法,再到今天的基于神经网络(编码-解码)的方法,逐渐形成了一套比较严谨的方法体系。
2. Word vectors
word embedding = word vectors = word representations
文本表示分为离散表示和分布式表示:
2.1 离散表示
-
One-hot,简称独热向量编码,也是特征工程中最常用的方法。每个分词的文本表示为“该分词的比特位为1,其余位为0”的矩阵表示。缺点:无法表示词语之间的相似性。语料库增加,向量维度更大。
-
Bag-of-word model,词袋模型。文档的向量表示是各词的词向量表示的加和。缺点是词与词之间没有顺序关系。
-
TF-IDF(term frequency–inverse document frequency),在信息检索与数据挖掘常用的加权技术。TF意思是词频,IDF意思是逆文本频率指数。缺点:没有体现词与词之间的关系顺序。

-
n-gram模型。为了保持词的顺序,做了一个滑窗,n是窗口大小。每个窗口为一组,组成字典。缺点:随着n增大,词表大小呈指数型增大。
2.2 分布式表示
用一个词附近的其它词来表示该词,这是现代统计自然语言处理中最有创见的想法之一。
Neural Network Language model
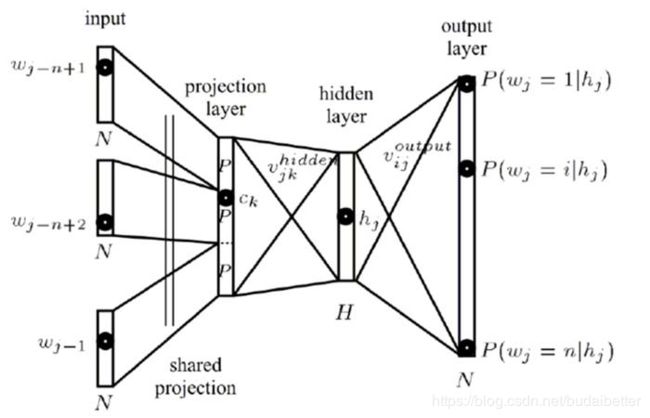
NNLM (Neural Network Language model),神经网络语言模型,通过训练得到词向量矩阵。
NNLM说的是定义一个前向窗口大小k,把这个窗口中最后一个词当做y,之前的词当做输入x。通俗来说就是通过这个窗口中的前k-1个词,预测最后一个词出现概率的模型。
SVD Based Methods
这是一类找到词向量的方法。首先遍历一个很大的数据集,统计词的共现计数矩阵 X,然后对矩阵 X 进行 SVD 分解得到 USV^T。然后我们使用 U 的行来作为字典中所有词的词向量。矩阵X有几种选择:
- Word-Document Matrix。我们猜想相关连的单词在同一个文档中会经常出现,所以矩阵 X 是按照以下方式构建:遍历数亿的文档,当词 i 出现在文档 j, Xij 加 1 。它的规模是和文档数量 M 成正比关系。
- Window based Co-occurrence Matrix。矩阵 X 存储单词的共现,从而成为一个关联矩阵。计算每个单词在特定大小的窗口中出现的次数,对语料库中所有单词进行统计。
Applying SVD to the cooccurrence Matrix,对矩阵X使用SVD:
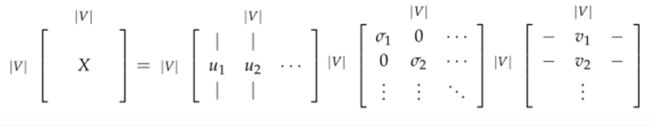
观察奇异值(矩阵 S 上对角线上元素),根据期望的捕获方差百分比截断,通过选择前 k 个奇异向量来降低维度:
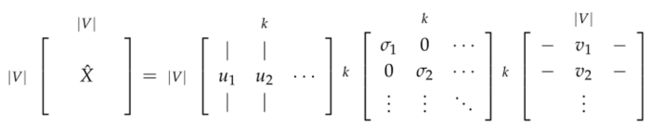
这两种方法都给我们提供了足够的词向量来编码语义和句法(part of speech)信息,但伴随许多其他问题
- 矩阵的维度会经常发生改变(经常增加新的单词和语料库的大小会改变)。
- 矩阵会非常的稀疏,因为很多词不会共现。
- 矩阵维度一般会非常高 ≈106×106≈106×106
- 基于 SVD 的方法的计算复杂度很高 ( m×nm×n 矩阵的计算成本是 O(mn2)O(mn2) ),并且很难合并新单词或文档
- 需要在 X 上加入一些技巧处理来解决词频的极剧的不平衡
这些问题存在以下的解决方法:
- 忽略功能词,例如 “the”,“he”,“has” 等等。
- 使用 ramp window,即根据文档中单词之间的距离对共现计数进行加权
- 使用皮尔逊相关系数并将负计数设置为0,而不是只使用原始计数
而基于迭代的方法以一种优雅得多的方式解决了大部分上述问题。
Word2vec - Iteration Based Methods
Word2vec是Google的Mikolov等人提出来的一种文本分布式表示的方法,巧妙地运用层次softmax(hierarchical softmax )和负采样(Negative sampling )两种技巧,使神经网络语言模型变得容易计算。
Word2vec的思路是设计一个模型,模型的参数就是词向量。然后根据一个目标函数训练模型,在每次模型的迭代计算误差,并遵循一些更新规则,该规则具有惩罚造成错误的模型参数的作用,从而可以学习到词向量。这个方法可以追溯到 1986年,我们称这个方法为“反向传播”,模型和任务越简单,训练它的速度就越快。
基于迭代的方法一次捕获一个单词的共现情况,而不是像SVD方法那样直接捕获所有的共现计数。
Word2vec概括地说是包含了两种模型和两种加速训练方法:
- 两种模型:CBOW(continuous bag-of-words)和Skip-Gram。CBOW的目标是通过上下文的词语预测中间的词是什么。而skip-gram则相反,由一个特定的词来预测前后可能出现的词。
- 两种优化方法:层次softmax和负采样。层次softmax是通过构建一种有效的树结构(哈夫曼树,huffman tree)来加速计算词语的概率分布的方法;而负采样则是通过随机抽取负样本,与正样本一起参加每次迭代,变成一个二分类问题而减少计算量的方法。
Word2vec的基础是语言模型,语言模型就是用来计算一个句子出现的概率。按链式法则,第k个词的出现取决于前k-1个词。如果引入马尔科夫模型来简化,则第k个词出现的概率只取决于前一个词。
CBOW
给定一对(上下文,中心词),已知中心词的one-hot是y©,也是模型输出的真实值。神经网络模型只有一个隐含层,我们需要得到两个矩阵,即输入层-隐含层 V、隐含层-输出层 U。
怎么得到这两个矩阵呢?这是神经网络参数求解的问题。首先初始化V和U,然后通过前后向传播得到收敛后的权重矩阵。最后得到的V也就是词向量矩阵。
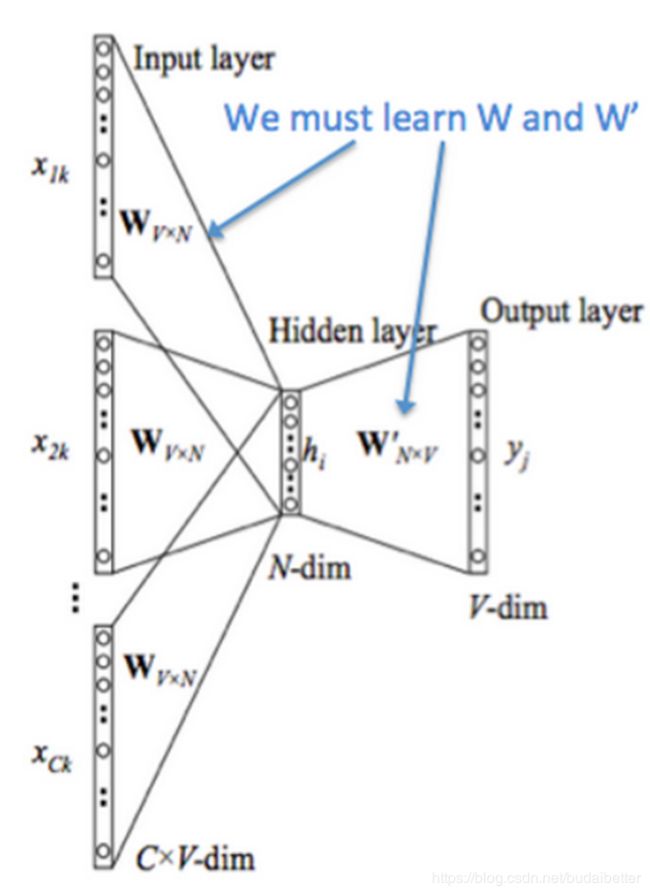
训练过程:
-
首先为大小为 m 的输入上下文生成 one-hot 词向量
-
乘以矩阵V得到上下文嵌入词向量
v c − m = V x ( c − m ) , v c − m + 1 = V x ( c − m + 1 ) , . . . , v c + m = V x ( c + m ) ∈ R n v_{c-m}=\mathcal{V}x^{(c-m)},\\v_{c-m+1}=\mathcal{V}x^{(c-m+1)},\\...,\\v_{c+m}=\mathcal{V}x^{(c+m)}\in \mathbb{R}^{n} vc−m=Vx(c−m),vc−m+1=Vx(c−m+1),...,vc+m=Vx(c+m)∈Rn -
然后对上述2m个向量求平均值,不进行非线性变换
v ^ = v c − m + v c − m + 1 + . . . + v c + m 2 m ∈ R n \widehat{v}=\frac{v_{c-m}+v_{c-m+1}+...+v_{c+m}}{2m}\in \mathbb{R}^{n} v =2mvc−m+vc−m+1+...+vc+m∈Rn
-
隐含层的输出乘以U求出得分向量z,再进行softmax得到中心词的概率分布。
z = U v ^ ∈ R ∣ V ∣ z = \mathcal {U}\widehat{v}\in \mathbb{R}^{|V|} z=Uv ∈R∣V∣y ^ = s o f t m a x ( z ) ∈ R ∣ V ∣ \widehat{y}=softmax(z)\in \mathbb{R}^{|V|} y =softmax(z)∈R∣V∣
-
用交叉熵损失(cross entropy)度量两个概率分布的差异。由于y是one-hot向量,后面可以化简。
H ( y ^ , y ) = − ∑ j = 1 ∣ V ∣ y j log ( y ^ j ) = − y c l o g ( y ^ c ) = − l o g ( y ^ c ) H(\hat{y}, y)=-\sum_{j=1}^{|V|} y_{j} \log \left(\hat{y}_{j}\right)= - y_{c}\,log(\widehat{y}_{c}) = -log(\widehat{y}_{c}) H(y^,y)=−j=1∑∣V∣yjlog(y^j)=−yclog(y c)=−log(y c)
c是正确词的one-hot向量的索引。 -
通过最小化交叉熵损失函数得到要优化的目标函数。
minimize J = − log P ( w c ∣ w c − m , … , w c − 1 , w c + 1 , … , w c + m ) = − log P ( u c ∣ v ^ ) = − log exp ( u c T v ^ ) ∑ j = 1 ∣ V ∣ exp ( u j T v ^ ) = − u c T v ^ + log ∑ j = 1 ∣ V ∣ exp ( u j T v ^ ) \begin{aligned} \text { minimize } J &=-\log P\left(w_{c} | w_{c-m}, \ldots, w_{c-1}, w_{c+1}, \ldots, w_{c+m}\right) \\ &=-\log P\left(u_{c} | \hat{v}\right) \\ &=-\log \frac{\exp \left(u_{c}^{T} \hat{v}\right)}{\sum_{j=1}^{|V|} \exp \left(u_{j}^{T} \hat{v}\right)} \\ &=-u_{c}^{T} \hat{v}+\log \sum_{j=1}^{|V|} \exp \left(u_{j}^{T} \hat{v}\right) \end{aligned} minimize J=−logP(wc∣wc−m,…,wc−1,wc+1,…,wc+m)=−logP(uc∣v^)=−log∑j=1∣V∣exp(ujTv^)exp(ucTv^)=−ucTv^+logj=1∑∣V∣exp(ujTv^) -
然后用SGD来更新u_c和w_j,SGD 对一个窗口计算梯度和更新参数,直到收敛。
U new ← U old − α ∇ U J V old ← V old − α ∇ V J \begin{array}{l}{\mathcal{U}_{\text {new}} \leftarrow \mathcal{U}_{\text {old}}-\alpha \nabla_{\mathcal{U}} J} \\ {\mathcal{V}_{\text {old}} \leftarrow \mathcal{V}_{\text {old}}-\alpha \nabla_{\mathcal{V}} J}\end{array} Unew←Uold−α∇UJVold←Vold−α∇VJ
CBOW模型中计算量大的地方是目标函数中是softmax,有V个词,所以要计算V个softmax,这也是之后改进时的重点。
Skip-Gram
Skip-Gram模型与CBOW大体相同,但是交换了我们的 x 和 y,对于给定的一个中心词,要预测上下文词。我们定义的权重矩阵(或者说词向量矩阵) V 和 U 是和 CBOW 一样的。
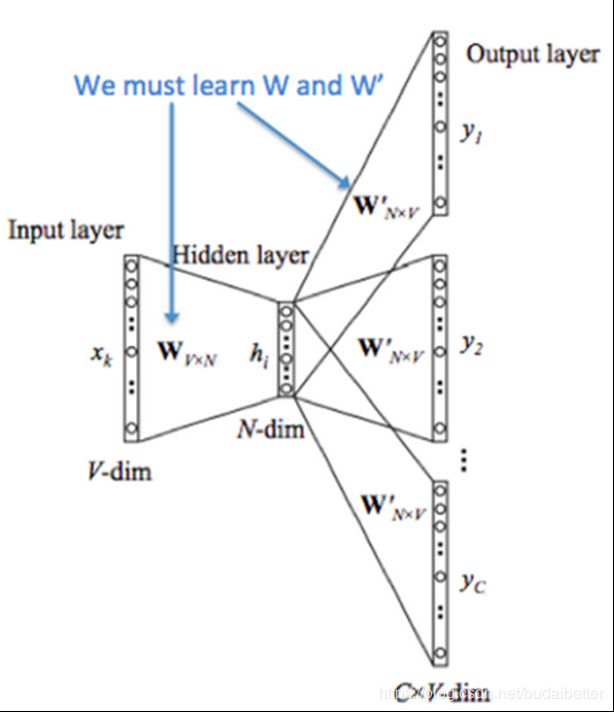
训练过程:
-
生成中心词的one-hot向量
-
把它乘以V矩阵,得到词嵌入向量,作为隐含层的输出
-
隐含层的输出乘以2m个U矩阵,生成分数向量 z
-
经过y^=softmax(z) 将分数向量转化为概率分布向量, y^是每个上下文词观察到的概率
-
生成一个目标函数来评估这个模型,这里与CBOW不同,引用了一个朴素贝叶斯假设来拆分概率。这是一个很强(朴素)的条件独立假设。换而言之,给定中心词,所有输出的词是完全独立的。
minimize J = − log P ( w c − m , … , w c − 1 , w c + 1 , … , w c + m ∣ w c ) = − log ∏ j = 0 , j ≠ m 2 m P ( w c − m + j ∣ w c ) = − log ∏ j = 0 , j ≠ m 2 m P ( u c − m + j ∣ v c ) = − log ∏ j = 0 , j ≠ m 2 m exp ( u c − m + j T v c ) ∑ k = 1 ∣ V ∣ exp ( u k T v c ) = − ∑ j = 0 , j ≠ m 2 m u c − m + j T v c + 2 m log ∑ k = 1 ∣ V ∣ exp ( u k T v c ) \begin{aligned} \text { minimize } J &=-\log P\left(w_{c-m}, \ldots, w_{c-1}, w_{c+1}, \ldots, w_{c+m} | w_{c}\right) \\ &=-\log \prod_{j=0, j \neq m}^{2 m} P\left(w_{c-m+j} | w_{c}\right) \\ &=-\log \prod_{j=0, j \neq m}^{2 m} P\left(u_{c-m+j} | v_{c}\right) \\ &=-\log \prod_{j=0, j \neq m}^{2 m} \frac{\exp \left(u_{c-m+j}^{T} v_{c}\right)}{\sum_{k=1}^{|V|} \exp \left(u_{k}^{T} v_{c}\right)} \\ &=-\sum_{j=0, j \neq m}^{2 m} u_{c-m+j}^{T} v_{c}+2 m \log \sum_{k=1}^{|V|} \exp \left(u_{k}^{T} v_{c}\right) \end{aligned} minimize J=−logP(wc−m,…,wc−1,wc+1,…,wc+m∣wc)=−logj=0,j=m∏2mP(wc−m+j∣wc)=−logj=0,j=m∏2mP(uc−m+j∣vc)=−logj=0,j=m∏2m∑k=1∣V∣exp(ukTvc)exp(uc−m+jTvc)=−j=0,j=m∑2muc−m+jTvc+2mlogk=1∑∣V∣exp(ukTvc)
通过这个目标函数,我们可以计算出与未知参数相关的梯度,并且在每次迭代中通过 SGD 来更新它们。 -
计算y^与上下文词真实的one-hot的交叉熵损失,然后求和,用来度量误差。
J = − ∑ j = 0 , j ≠ m 2 m log P ( u c − m + j ∣ v c ) = ∑ j = 0 , j ≠ m 2 m H ( y ^ , y c − m + j ) \begin{aligned} J &=-\sum_{j=0, j \neq m}^{2 m} \log P\left(u_{c-m+j} | v_{c}\right) \\ &=\sum_{j=0, j \neq m}^{2 m} H\left(\hat{y}, y_{c-m+j}\right) \end{aligned} J=−j=0,j=m∑2mlogP(uc−m+j∣vc)=j=0,j=m∑2mH(y^,yc−m+j)
其中H()是向量y^的概率和one-hot向量y_{c-m+1}之间的交叉熵。
负采样
在CBOW和Skip-Gram中,目标函数要计算V个softmax值,注意对 |V| 的求和计算量是非常大的。任何的更新或者对目标函数的评估都要花费 O(|V|) 的时间复杂度。一个简单的想法是不去直接计算,而是去求近似值。
负采样的思想就是,在每一个训练的时间步,我们不去遍历整个词汇表,而仅仅是抽取一些负样例。将词典中的每一个词对应一条线段,所有词组成了[0,1]之间的剖分,如下图所示。然后每次随机生成一个[1, M-1]间的整数,看落在哪个词上就选择哪个词,最后会得到一个负样本集合。
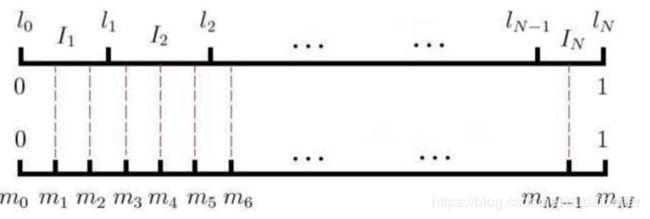
虽然负采样是基于 Skip-Gram 模型,但实际上是对一个不同的目标函数进行优化。
考虑一对中心词和上下文词(w,c) 。这词对是来自训练数据集吗?我们通过 P(D=1∣w,c) 表示 (w,c) 是来自语料库。相应地, P(D=0∣w,c)表示 (w,c) 不是来自语料库。
首先,我们对 P(D=1∣w,c) 用 sigmoid 函数建模:
P ( D = 1 ∣ w , c , θ ) = σ ( v c T v w ) = 1 1 + e ( − v c T v w ) P(D=1 | w, c, \theta)=\sigma\left(v_{c}^{T} v_{w}\right)=\frac{1}{1+e^{\left(-v_{c}^{T} v_{w}\right)}} P(D=1∣w,c,θ)=σ(vcTvw)=1+e(−vcTvw)1
现在,我们建立一个新的目标函数,如果中心词和上下文词确实在语料库中,就最大化概率 P(D=1∣w,c),如果中心词和上下文词确实不在语料库中,就最大化概率 P(D=0∣w,c) 。我们对这两个概率采用一个简单的极大似然估计的方法(这里我们把 θ 作为模型的参数,在我们的例子是 V 和 U )
θ = argmax θ ∏ ( w , c ) ∈ D P ( D = 1 ∣ w , c , θ ) ∏ ( w , c ) ∈ D ~ P ( D = 0 ∣ w , c , θ ) = argmax θ ∏ ( w , c ) ∈ D P ( D = 1 ∣ w , c , θ ) ∏ ( w , c ) ∈ D ~ ( 1 − P ( D = 1 ∣ w , c , θ ) ) = argmax θ ∑ ( w , c ) ∈ D log P ( D = 1 ∣ w , c , θ ) + ∑ ( w , c ) ∈ D ~ log ( 1 − P ( D = 1 ∣ w , c , θ ) ) = arg max θ ∑ ( w , c ) ∈ D log 1 1 + exp ( − u w T v c ) + ∑ ( w , c ) ∈ D ~ log ( 1 − 1 1 + exp ( − u w T v c ) ) = arg max θ ∑ ( w , c ) ∈ D log 1 1 + exp ( − u w T v c ) + ∑ ( w , c ) ∈ D ~ log ( 1 1 + exp ( u w T v c ) ) \begin{aligned} \theta &=\underset{\theta}{\operatorname{argmax}} \prod_{(w, c) \in D} P(D=1 | w, c, \theta) \prod_{(w, c) \in \widetilde{D}} P(D=0 | w, c, \theta) \\ &=\underset{\theta}{\operatorname{argmax}} \prod_{(w, c) \in D} P(D=1 | w, c, \theta) \prod_{(w, c) \in \widetilde{D}}(1-P(D=1 | w, c, \theta)) \\ &=\underset{\theta}{\operatorname{argmax}} \sum_{(w, c) \in D} \log P(D=1 | w, c, \theta)+\sum_{(w, c) \in \widetilde{D}} \log (1-P(D=1 | w, c, \theta)) \\ &=\arg \max _{\theta} \sum_{(w, c) \in D} \log \frac{1}{1+\exp \left(-u_{w}^{T} v_{c}\right)}+\sum_{(w, c) \in \widetilde{D}} \log \left(1-\frac{1}{1+\exp \left(-u_{w}^{T} v_{c}\right)}\right) \\ &=\arg \max _{\theta} \sum_{(w, c) \in D} \log \frac{1}{1+\exp \left(-u_{w}^{T} v_{c}\right)}+\sum_{(w, c) \in \widetilde{D}} \log \left(\frac{1}{1+\exp \left(u_{w}^{T} v_{c}\right)}\right) \end{aligned} θ=θargmax(w,c)∈D∏P(D=1∣w,c,θ)(w,c)∈D ∏P(D=0∣w,c,θ)=θargmax(w,c)∈D∏P(D=1∣w,c,θ)(w,c)∈D ∏(1−P(D=1∣w,c,θ))=θargmax(w,c)∈D∑logP(D=1∣w,c,θ)+(w,c)∈D ∑log(1−P(D=1∣w,c,θ))=argθmax(w,c)∈D∑log1+exp(−uwTvc)1+(w,c)∈D ∑log(1−1+exp(−uwTvc)1)=argθmax(w,c)∈D∑log1+exp(−uwTvc)1+(w,c)∈D ∑log(1+exp(uwTvc)1)
注意最大化似然函数等同于最小化负对数似然:
J = − ∑ ( w , c ) ∈ D log 1 1 + exp ( − u w T v c ) − ∑ ( w , c ) ∈ D ~ log ( 1 1 + exp ( u w T v c ) ) J=-\sum_{(w, c) \in D} \log \frac{1}{1+\exp \left(-u_{w}^{T} v_{c}\right)}-\sum_{(w, c) \in \widetilde{D}} \log \left(\frac{1}{1+\exp \left(u_{w}^{T} v_{c}\right)}\right) J=−(w,c)∈D∑log1+exp(−uwTvc)1−(w,c)∈D ∑log(1+exp(uwTvc)1)
注意 ˜D 是“假的”或者“负的”语料。
对于 Skip-Gram 模型,我们对给定中心词 c 来观察的上下文单词 c−m+j 的新目标函数为
− log σ ( u c − m + j T ⋅ v c ) − ∑ k = 1 K log σ ( − u ~ k T ⋅ v c ) -\log \sigma\left(u_{c-m+j}^{T} \cdot v_{c}\right)-\sum_{k=1}^{K} \log \sigma\left(-\tilde{u}_{k}^{T} \cdot v_{c}\right) −logσ(uc−m+jT⋅vc)−k=1∑Klogσ(−u~kT⋅vc)
对 CBOW 模型,我们对给定上下文向量
v ^ = v c − m + v c − m + 1 + . . . + v c + m 2 m \widehat{v}=\frac{v_{c-m}+v_{c-m+1}+...+v_{c+m}}{2m} v =2mvc−m+vc−m+1+...+vc+m
来观察中心词 u_c 的新的目标函数为
− l o g σ ( u c T ⋅ v ^ ) − ∑ k = 1 K l o g σ ( − u ~ k T ⋅ v ^ ) -log\,\sigma(u_{c}^{T}\cdot \widehat{v})-\sum_{k=1}^{K}log\,\sigma(-\widetilde{u}_{k}^{T}\cdot \widehat{v}) −logσ(ucT⋅v )−k=1∑Klogσ(−u kT⋅v )
在上面的公式中,{˜u_k∣k=1…K}是从 P_n(w) 中抽样。有很多关于如何得到最好近似的讨论,从实际效果看来最好的是指数为 ¾ 的 Unigram 模型。那么为什么是 ¾?下面有一些例如可能让你有一些直观的了解:
i s : 0. 9 3 4 = 0.92 C o n s t i t u t i o n : 0.0 9 3 4 = 0.16 b o m b a s t i c : 0.0 1 3 4 = 0.032 is: 0.9^{\frac34}=0.92 \\ Constitution: 0.09^{\frac34}=0.16 \\ bombastic: 0.01^{\frac34}=0.032 is:0.943=0.92Constitution:0.0943=0.16bombastic:0.0143=0.032
“Bombastic”现在被抽样的概率是之前的三倍,而“is”只比之前的才提高了一点点。
层次softmax
hierarchical softmax相比普通的softmax是一种更有效的替代方法。hierarchical softmax 对低频词往往表现得更好,负采样对高频词和较低维度向量表现得更好。
Hierarchical softmax 使用一个二叉树来表示词表中的所有词。使用Huffman Tree来编码输出层的词典,相当于平铺到各个叶子节点上,瞬间把维度降低到了树的深度。树中的每个叶结点都是一个单词,而且只有一条路径从根结点到叶结点。在这个模型中,没有词的输出表示。相反,图的每个节点(根节点和叶结点除外)与模型要学习的向量相关联。单词作为输出单词的概率定义为从根随机游走到单词所对应的叶的概率。计算成本变为 O(log(|V|))而不是 O(|V|),对应着路径的长度。
下图是 Hierarchical softmax 的二叉树示意图:
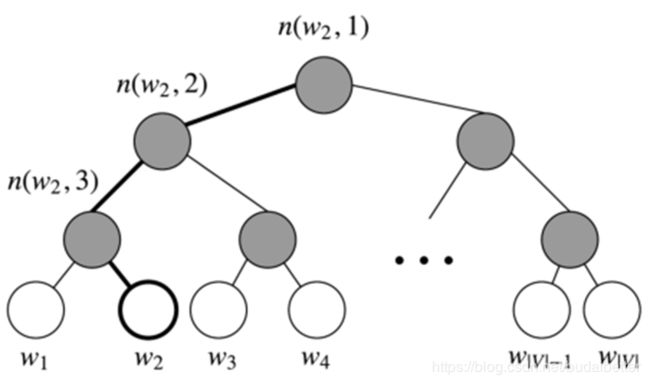
令 L(w) 为从根结点到叶结点 w 的路径中节点数目。我们定义 n(w,i) 为与向量 v_{n(w,i)}相关的路径上第 i 个结点。因此 n(w,1) 是根结点,而 n(w,L(w)) 是 w 的父节点。现在对每个内部节点 n,我们任意选取一个它的子节点,定义为 ch(n) (一般是左节点)。然后,我们可以计算概率为
p ( w ∣ w i ) = ∏ j = 1 L ( w ) − 1 σ ( [ n ( w , j + 1 ) = ch ( n ( w , j ) ) ] ⋅ v n ( w , j ) T v w i ) 其 中 [ x ] = { 1 if x is true − 1 otherwise p\left(w | w_{i}\right)=\prod_{j=1}^{L(w)-1} \sigma\left([n(w, j+1)=\operatorname{ch}(n(w, j))] \cdot v_{n(w, j)}^{T} v_{w_{i}}\right) \\ 其中 \ [x]=\left\{\begin{array}{ll}{1} & {\text { if } x \text { is true }} \\ {-1} & {\text { otherwise }}\end{array}\right. p(w∣wi)=j=1∏L(w)−1σ([n(w,j+1)=ch(n(w,j))]⋅vn(w,j)Tvwi)其中 [x]={1−1 if x is true otherwise
如果我们假设 ch(n) 一直都是 n 的左节点,然后当路径往左时 [n(w,j+1)=ch(n(w,j)) ] 的值返回 1,往右则返回 0。以上图中的 w2 为例,从根节点要经过两次左边的边和一次右边的边才到达 w2 ,因此
p ( w 2 ∣ w i ) = p ( n ( w 2 , 1 ) , left ) ⋅ p ( n ( w 2 , 2 ) , left ) ⋅ p ( n ( w 2 , 3 ) , right ) = σ ( v n ( w 2 , 1 ) T v w i ) ⋅ σ ( v n ( w 2 , 2 ) T v w i ) ⋅ σ ( − v n ( w 2 , 3 ) T v w i ) \begin{aligned} p\left(w_{2} | w_{i}\right) &=p\left(n\left(w_{2}, 1\right), \text {left}\right) \cdot p\left(n\left(w_{2}, 2\right), \text {left}\right) \cdot p\left(n\left(w_{2}, 3\right), \text { right }\right) \\ &=\sigma\left(v_{n\left(w_{2}, 1\right)}^{T} v_{w_{i}}\right) \cdot \sigma\left(v_{n\left(w_{2}, 2\right)}^{T} v_{w_{i}}\right) \cdot \sigma\left(-v_{n\left(w_{2}, 3\right)}^{T} v_{w_{i}}\right) \end{aligned} p(w2∣wi)=p(n(w2,1),left)⋅p(n(w2,2),left)⋅p(n(w2,3), right )=σ(vn(w2,1)Tvwi)⋅σ(vn(w2,2)Tvwi)⋅σ(−vn(w2,3)Tvwi)
我们训练模型的目标是最小化负的对数似然 −logP(w∣wi) 。不是更新每个词的输出向量,而是更新二叉树中从根结点到叶结点的路径上的节点的向量。
该方法的速度由构建二叉树的方式确定,并将词分配给叶节点。Mikolov 在论文《Distributed Representations of Words and Phrases and their Compositionality.》中使用的是哈夫曼树,在树中分配高频词到较短的路径。
Word2vec存在的问题
- 对每个local context window单独训练,没有利用包 含在global co-currence矩阵中的统计信息。
- 对多义词无法很好的表示和处理,因为使用了唯一的词向量
.
.
.
参考:
CS224n 01 Introduction and Word Vectors
文本分布式表示(一):word2vec理论
https://github.com/NLP-LOVE/ML-NLP
https://looperxx.github.io