利用scipy.optimize.curve_fit对函数进行拟合

文档

基本使用

用样本拟合函数$f(x)=a{e}^{-bx}+c$

# 将图片内嵌在交互窗口，而不是弹出一个图片窗口
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

# 定义目标函数
def func(x, a, b, c):
    return a * np.exp(-b * x) + c

# 这部分生成样本点，对函数值加上高斯噪声作为样本点
# [0, 4]共50个点
xdata = np.linspace(0, 4, 50)
# a=2.5, b=1.3, c=0.5
y = func(xdata, 2.5, 1.3, 0.5)
np.random.seed(10086)
err_stdev = 0.2
# 生成均值为0，标准差为err_stdev为0.2的高斯噪声
y_noise = err_stdev * np.random.normal(size=xdata.size)
ydata = y + y_noise
plt.figure('拟合图')
plt.plot(xdata, ydata, 'b-', label='data')


# 利用curve_fit作简单的拟合，popt为拟合得到的参数,pcov是参数的协方差矩阵
popt, pcov = curve_fit(func, xdata, ydata)
plt.plot(xdata, func(xdata, *popt), 'r-', label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))


# 限定参数范围：0<=a<=3, 0<=b<=1, 0<=c<=0.5
popt, pcov = curve_fit(func, xdata, ydata, bounds=(0, [3., 1., 0.5]))
plt.plot(xdata, func(xdata, *popt), 'g--', label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))

plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()

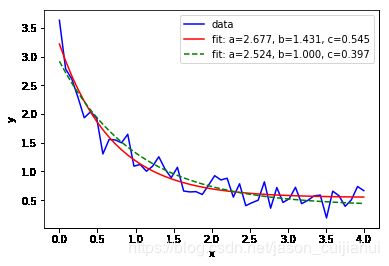
结果

样本的生成方式为$f(x)=2.5e^{-1.3x}+0.5$

# pfit为估计参数值的期望
# perr为估计参数值的标准差

# a=2.67723696 +/- 0.11148278
# b=1.43052196 +/- 0.12346413
# c=0.54537768 +/- 0.04397317
pfit(case 1) [2.67723696 1.43052196 0.54537768]
perr(case 1) [0.11148278 0.12346413 0.04397317]


pfit(case 2) [2.52418114 1.         0.39663756]
perr(case 2) [0.11186864 0.11340588 0.07113215]

• 普通拟合的结果为$f(x)=2.677e^{-1.431x}+0.545$
• 参数范围受限拟合的结果为$f(x)=2.524e^{-x}+0.397$

从结果来看还是拟合得不错的

计算拟合结果的指标

• SSE(和方差、误差平方和)
  
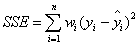
• MSE(均方差、方差)
  
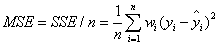
• RMSE(均方根、标准差)
  
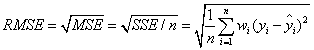
• R-square(决定系数) （R-square不适合用于判断非线性拟合的效果）
  $R^2$捕捉是的线性关系。如某学生在某智力量表上所得的 IQ 分与其学业成绩的相关系数 $r=0.66$，则决定系数 $R^2=0.4356$，即该生学业成绩约有 44%可由该智力量表所测的智力部分来说明或决定。
  $0\le R^2\le 1$，越接近1时，拟合效果越好
  
  
  
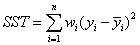
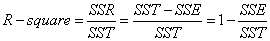
• Adjusted R-square(校正决定系数)：Degree-of-freedom adjusted coefficient of determination
  如果用决定系数R方来评价回归方程的优劣，会出现如下问题：随着自变量个数的增加，R将不断增大（即模型复杂度越高，则R方越大）。下面为校正决定系数的公式，n为样本个数，p为特征个数。
  

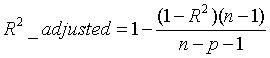
def getIndexes(y_predict, y_data):
    n = y_data.size
    # SSE为和方差
    SSE=((y_data-y_predict)**2).sum()
    # MSE为均方差
    MSE=SSE/n
    # RMSE为均方根,越接近0，拟合效果越好
    RMSE=np.sqrt(MSE)
    
    # 求R方，0<=R<=1，越靠近1,拟合效果越好
    u = y_data.mean()
    SST=((y_data-u)**2).sum()
    SSR=SST-SSE
    R_square=SSR/SST
    return SSE, MSE, RMSE, R_square

比较上一节的两次拟合，哪个拟合得更好

# 模型1
y_predict_1=func(xdata, *popt_1)
indexes_1=getIndexes(y_predict_1, ydata)
# (1.547750647353422, 0.030955012947068438, 0.1759403675881929, 0.9361164947913276)
print(indexes_1)

# 模型2
y_predict_2=func(xdata, *popt_2)
indexes_2=getIndexes(y_predict_2, ydata)
# (1.9852184554460819, 0.03970436910892164, 0.1992595521146267, 0.9180599835279003)
print(indexes_2)

关于样本噪声的先验知识

在我们前面，我们的拟合方式是测试出来的ydata是真实的值，并没有噪声的干扰。

然而，我们从上帝视角可以看到，测试出来的ydata是真实值和高斯噪声的叠加，如果我们有这个先验知识，那么是可以更好地拟合出真实的曲线。(这个好是从上面拟合结果的指标是看不出来的)在我们的例子里，高斯噪声的标准差为err_stdev，我们在拟合的时候加入此先验知识。

# 利用curve_fit作简单的拟合，popt为拟合得到的参数
popt_1, pcov_1 = curve_fit(func, xdata, ydata, sigma=err_stdev*np.ones(ydata.size), absolute_sigma=True)
plt.plot(xdata, func(xdata, *popt_1), 'r-', label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt_1))
# 取出pcov_1矩阵的对角元素，开方得到各个参数估计的标准差
print('pfit(case 1)', popt_1)
print('perr(case 1)', np.sqrt(np.diag(pcov_1)))

# 限定参数范围：0<=a<=3, 0<=b<=1, 0<=c<=0.5
popt_2, pcov_2 = curve_fit(func, xdata, ydata, sigma=err_stdev*np.ones(ydata.size), absolute_sigma=True, bounds=(0, [3., 1., 0.5]))
plt.plot(xdata, func(xdata, *popt_2), 'g--', label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt_2))
# 取出pcov_2矩阵的对角元素，开方得到各个参数估计的标准差
print('pfit(case 2)', popt_2)
print('perr(case 2)', np.sqrt(np.diag(pcov_2)))

结果：

# 我们可以看到两个模型的perr都比之前的大，说明拟合结果没之前想象中的那么好
# 这是符合逻辑的，当我们意识到样本值的偏差，明白问题本身具有未意识前更高的难度
pfit(case 1) [2.67723696 1.43052196 0.54537768]
perr(case 1) [0.12286728 0.13607215 0.04846366]
pfit(case 2) [2.52418114 1.         0.39663756]
perr(case 2) [0.10886371 0.11035966 0.06922146]

可以选取参数的初始取值，可能会得到更好的拟合结果