使用python求解特征值与特征向量
使用python求解特征值与特征向量
问题描述:
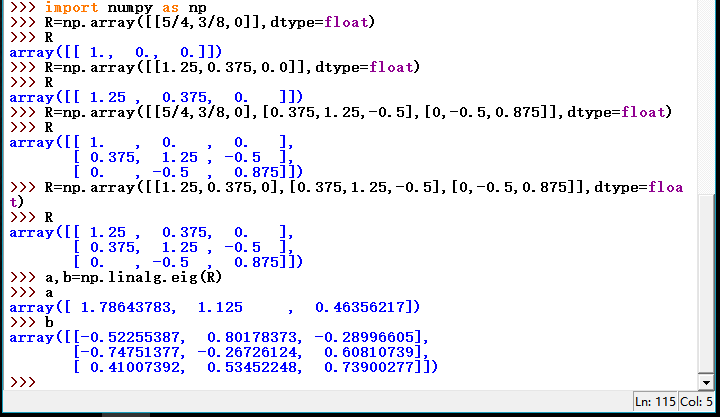
求解矩阵[[1.25,0.375,0],[0.375,1.25,-0.5],[0,-0.5,0.875]]的特征值与特征向量
参考链接1:
百度经验:python线性代数—求方阵的特征值特征向量
利用python求解方阵特征值与特征向量的方法及代码实现
>>>import numpy as np ##引入numpy模块
>>>x=numpy.diag((1,2,3)) ##写入对角阵x
>>>x ##输出对角阵x
array([[1,0,0],
[0,2,0],
[0,0,3]])
>>>a,b=numpy.linalg.elg(x) ##特征值赋值给a,对应特征向量赋值给b
>>>a ##特征值 1 2 3
array([1.,2.,3.])
>>>b ##特征向量
array([1.,0.,0.],
[0.,1.,0.],
[0.,0.,1.]) 局限性:使用函数numpy.diag( )产生的是对角阵,实际情况都是要处理一般方阵。关于numpy.diag( )的用法可以参考numpy.diag 使用说明
参考链接2:
科学计算python VS matlab
介绍python进行矩阵运算的各种函数
a2=np.array([[1,2,3],[2,3,4]]) #建立一个二维数组
b2=np.array([[1,2,3],[2,3,4]],dtype=int) #可以输出指定数据类型
np.linalg.eig(a2) #返回矩阵a2的特征值与特征向量参考链接3:
特征值与特征向量的雅克比算法C++实现
没有比较就不知道,使用python求解特征值问题多么简单!
链接3是使用C++求解特征值的方法,虽然有点复杂,代码多,个人感觉,有必要看一看,以认识具体的实现过程。
来点总结:
1、被自己感动了!
2、python使用的确方便!
3、网络真是学习的宝库啊,任何资源都能找到!