LearnGL - 11.5 - 矩阵04 - 法线从对象空间变换到世界空间
文章目录
- Unity 中的处理
- OpenGL 处理
- 为何要使用 IT_mMat
- 总结
- References
LearnGL - 学习笔记目录
前些篇:
- LearnGL - 11.1 - 实现简单的Gouraud-Phong光照模型
- LearnGL - 11.2 - 实现简单的Phong光照模型
- LearnGL - 11.3 - 实现简单的Blinn-Phong光照模型
- LearnGL - 11.4 - 实现简单的Flat BlinnPhong光照模型
了解了 Gouraud-Phong、Phong、Blinn-Phong、Flat Blinn-Phong 光照模型的基本认识。
这篇:我们重点讲解一下 法线从对象空间变换到世界空间 的变换矩阵的推导过程,因为之前四篇光照处理有用到,但没有细节的去讲解到。
本人才疏学浅,如有什么错误,望不吝指出。
Unity 中的处理
在 Unity ShaderLab 中,你可能会看到内置的函数:
// Transforms normal from object to world space
inline float3 UnityObjectToWorldNormal( in float3 norm )
{
#ifdef UNITY_ASSUME_UNIFORM_SCALING
return UnityObjectToWorldDir(norm);
#else
// mul(IT_M, norm) => mul(norm, I_M) => {dot(norm, I_M.col0), dot(norm, I_M.col1), dot(norm, I_M.col2)}
return normalize(mul(norm, (float3x3)unity_WorldToObject));
#endif
}
这函数中:
#ifdef UNITY_ASSUME_UNIFORM_SCALING
return UnityObjectToWorldDir(norm);
#else
是处理统一缩放的法线变换,所以我们聚焦在后面那块:
// mul(IT_M, norm) => mul(norm, I_M) => {dot(norm, I_M.col0), dot(norm, I_M.col1), dot(norm, I_M.col2)}
return normalize(mul(norm, (float3x3)unity_WorldToObject));
unity_WorldToObject model matrix 的逆矩阵,然后我们用 float3 * float3x3 来免去了处理 transpose(unity_WorldToObject) 的转置处理,像上面那句也可以这么写,但没必要:
return normalize(mul(transpose((float3x3)unity_WorldToObject), norm));
即: float3x3 * float3 的意思
OpenGL 处理
在我之前的一些 LearnGL 系列笔记中,如:LearnGL - 11.1 - 实现简单的Gouraud-Phong光照模型,写了一个 GLSL 函数 vec3 ObjectToWorldNormal(vec3 n):
// 将对象空间的法线转换到世界空间下的法线
vec3 ObjectToWorldNormal(vec3 n) {
return normalize(mat3(IT_mMat) * n); // 等价于:transpose(I_mMat) * vec4(n, 0)
}
(这里顺便吐槽一下,GLSL 中竟然不支持 inline 内联开展?因为我编译 GLSL shader 是会提示:“inline” not supported 之类的,不会又需要什么 GL 的 Extensions 吧?)
这代码中的 IT_mMat 是我在 C++ 层计算好的 mMat 的 逆矩阵 的 转置矩阵,再传入到 shader 的 uniform,对应上面 Unity 中的 unity_WorldToObject,只不过 unity_WorldToObject 没有转置而已,只是 巧妙的利用了 CG/HLSL 中 mul 函数的特性来避免 transpose 函数的转置处理。
为何要使用 IT_mMat
那么为何我们要用 Model Matrix 的 逆矩阵的转置矩阵 来变换法线呢?
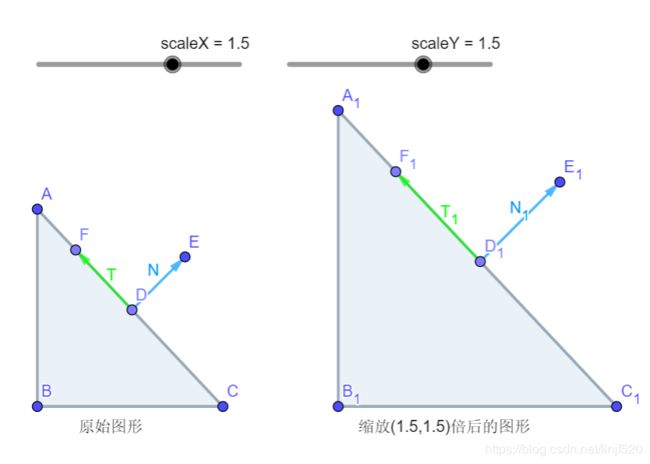
先来看看,我们变换顶点都是使用 mMat 从 对象空间 变换到 世界空间,那么如果我们使用这个 mMat 矩阵来变换法线可以吗?
上图,左边 原始图形 中的 T T T 是切线, N N N 是法线,右边 缩放后的图形 的 T 1 T_1 T1 是切线, N 1 N_1 N1 是法线
在统一缩放(缩放分量相同)看起来没有问题
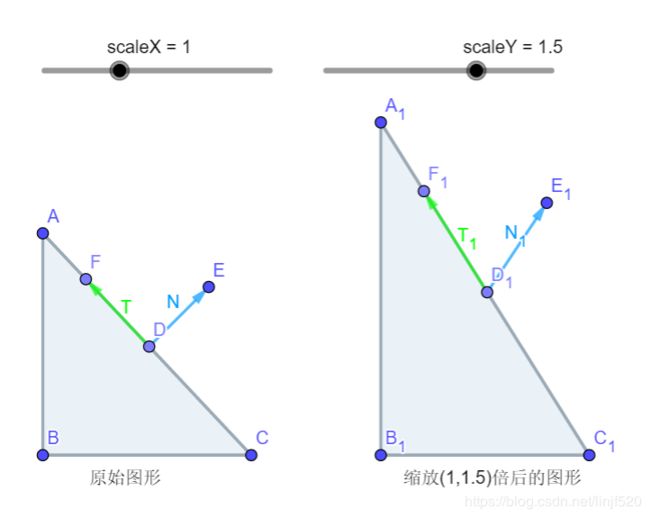
如果在非统一缩放呢?看看:
看起来 T 1 T_1 T1 还是 保持着 平面上的 切线,但是 N 1 N_1 N1 就 没有保持 与平面 垂直 了。
所以,在非统一缩放时,用 mMat 矩阵来变换法线是不行的。
那么我们利用一些已知的数学公式来推导:
已知:
- Model Matrix(对象到世界空间变换矩阵)
mMat,我们定义符号为: M m M_m Mm - T T T 是原始切线
- N N N 是原始法线
- T 1 T_1 T1 是 M m M_m Mm 变换后的切线
- N 1 N_1 N1 是 M n \red{M_n} Mn 变换后仍然垂直于平面的法线
M n \red{M_n} Mn 是目前不知道的,正式是我们要求的 法线变换矩阵,即:IT_mMat
由于法线是垂直于切线的,所以我们可以将一些公理式子列出来:
{ N T ⋅ T = 0 ( 1 ) 法线与切线的点积为0,因为相互垂直 N 1 T ⋅ T 1 = 0 ( 2 ) 变换后的法线与切线仍然是垂直的 T 1 = M m ⋅ T ( 3 ) T 1 是通过 M m 矩阵变换后得到的 N 1 = M n ⋅ N ( 4 ) N 1 是通过 M n 矩 阵 变 换 后 得 到 的 \begin{cases} N^T \cdot T=0 & (1) \text{法线与切线的点积为0,因为相互垂直}\\ N_1^T \cdot T_1=0 & (2) \text{变换后的法线与切线仍然是垂直的}\\ T_1=M_m \cdot T & (3)T_1\text{是通过}M_m\text{矩阵变换后得到的}\\ N_1=\red{M_n} \cdot N &(4)N_1\text{是通过}M_n矩阵变换后得到的 \end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧NT⋅T=0N1T⋅T1=0T1=Mm⋅TN1=Mn⋅N(1)法线与切线的点积为0,因为相互垂直(2)变换后的法线与切线仍然是垂直的(3)T1是通过Mm矩阵变换后得到的(4)N1是通过Mn矩阵变换后得到的
(上面关于点积 dot 可以参考我之前写的:LearnGL - 11.1 - 实现简单的Gouraud-Phong光照模型 - dot - 点积的作用)
我们将 ( 1 ) (1) (1)号等式左边部分在中间添加一个 I I I,那么结果为: N T ⋅ T = N T ⋅ I ⋅ T = 0 N^T \cdot T=N^T \cdot \red{I} \cdot T=0 NT⋅T=NT⋅I⋅T=0,其中 I \red{I} I 是单位矩阵
I = M m − 1 ⋅ M m I=M_m^{-1} \cdot M_m I=Mm−1⋅Mm 就是一个矩阵与它的逆矩阵变换后就抵消了矩阵的所有变换,没有变换的特性就是 单位矩阵 的特性,所以这个是没有问题的
所以: N T ⋅ T = N T ⋅ I ⋅ T → N T ⋅ T = N T ⋅ M m − 1 ⋅ M m ⋅ T = 0 N^T \cdot T=N^T \cdot \red{I} \cdot T \to N^T \cdot T=N^T \cdot \red{M_m^{-1}\cdot M_m} \cdot T=0 NT⋅T=NT⋅I⋅T→NT⋅T=NT⋅Mm−1⋅Mm⋅T=0
仔细观察公式中红色部分, N T ⋅ T = N T ⋅ M m − 1 ⋅ M m ⋅ T = 0 N^T \cdot T=N^T \cdot M_m^{-1}\cdot \red{M_m \cdot T}=0 NT⋅T=NT⋅Mm−1⋅Mm⋅T=0 中 的 M m ⋅ T \red{M_m \cdot T} Mm⋅T ,其实这部分就是 ( 3 ) (3) (3)等式右边的内容: T 1 = M m ⋅ T T_1=\red{M_m \cdot T} T1=Mm⋅T
所以我们的式子再次可以调整为: N T ⋅ T = N T ⋅ M m − 1 ⋅ T 1 = 0 N^T \cdot T=N^T \cdot M_m^{-1}\cdot \red{T_1}=0 NT⋅T=NT⋅Mm−1⋅T1=0
再次仔细观察一下 ( 2 ) : N 1 T ⋅ T 1 = 0 (2):N_1^T \cdot T_1=0 (2):N1T⋅T1=0与 N T ⋅ T = N T ⋅ M m − 1 ⋅ T 1 N^T \cdot T=N^T \cdot M_m^{-1}\cdot \red{T_1} NT⋅T=NT⋅Mm−1⋅T1 有什么共同之处?
{ N 1 T ⋅ T 1 = 0 ( 2 ) N T ⋅ T = N T ⋅ M m − 1 ⋅ T 1 = 0 ( 5 ) \begin{cases} N_1^T \cdot \red{T_1}=0 & (2)\\ \blue{N^T \cdot T}=N^T \cdot M_m^{-1}\cdot \red{T_1}=0 & (5) \end{cases} {N1T⋅T1=0NT⋅T=NT⋅Mm−1⋅T1=0(2)(5)
把 ( 5 ) (5) (5)等式左边(也就 蓝色 部分)的 N T ⋅ T \blue{N^T \cdot T} NT⋅T 去掉,变成下面的等式
{ N 1 T ⋅ T 1 = 0 ( 2 ) N T ⋅ M m − 1 ⋅ T 1 = 0 ( 5 ) \begin{cases} N_1^T \cdot &\red{T_1}=0 & (2)\\ N^T \cdot M_m^{-1}\cdot &\red{T_1}=0 & (5) \end{cases} {N1T⋅NT⋅Mm−1⋅T1=0T1=0(2)(5)
现在可以清晰看到 ( 2 ) (2) (2)和 ( 5 ) (5) (5)的红色部分的 T 1 \red{T_1} T1是相同的,那么剩下的部分我们标记上绿色:
{ N 1 T ⋅ T 1 = 0 ( 2 ) N T ⋅ M m − 1 ⋅ T 1 = 0 ( 5 ) \begin{cases} \green{N_1^T} \cdot &\red{T_1}=0 & (2)\\ \green{N^T \cdot M_m^{-1}}\cdot &\red{T_1}=0 & (5) \end{cases} {N1T⋅NT⋅Mm−1⋅T1=0T1=0(2)(5)
这绿色的部分,我们也可以认为他们是相等的
即: { N 1 T = N T ⋅ M m − 1 ( 6 ) \begin{cases}\green{N_1^T}=\green{N^T \cdot M_m^{-1}} & (6)\end{cases} {N1T=NT⋅Mm−1(6)
为了便于观察,将等式 左右 两个的内容 分别标记 为 红色、绿色
N 1 T = N T ⋅ M m − 1 \red{N_1^T}=\green{N^T \cdot M_m^{-1}} N1T=NT⋅Mm−1
再将等式两边同时转置一下:
( N 1 T ) T = ( N T ⋅ M m − 1 ) T (\red{N_1^T})^T=(\green{N^T \cdot M_m^{-1}})^T (N1T)T=(NT⋅Mm−1)T
左边 的 ( N 1 T ) T (\red{N_1^T})^T (N1T)T 本身有转置的,再次转置就抵消了,所以: ( N 1 T ) T = N 1 (\red{N_1^T})^T=\red{N_1} (N1T)T=N1
右边 的 ( N T ⋅ M m − 1 ) T (\green{N^T \cdot M_m^{-1}})^T (NT⋅Mm−1)T,由于 矩阵转置 的性质: ( A ⋅ B ) T = B T ⋅ A T (A\cdot B)^T=B^T\cdot A^T (A⋅B)T=BT⋅AT
所以后变成了: ( N T ⋅ M m − 1 ) T = ( M m − 1 ) T ⋅ ( N T ) T (\green{N^T \cdot M_m^{-1}})^T=\green{(M_m^{-1})}^T \cdot \green{(N^T)}^T (NT⋅Mm−1)T=(Mm−1)T⋅(NT)T
最后边的 ( N T ) T \green{(N^T)}^T (NT)T 转置的转置,所以抵消转置 ( N T ) T = N \green{(N^T)}^T=\green{N} (NT)T=N
所以 右边 ( N T ⋅ M m − 1 ) T = ( M m − 1 ) T ⋅ N (\green{N^T \cdot M_m^{-1}})^T=\green{(M_m^{-1})^T \cdot N} (NT⋅Mm−1)T=(Mm−1)T⋅N
最终 ( 6 ) (6) (6)号等式 左右两边,变成了: N 1 = ( M m − 1 ) T ⋅ N \red{N_1}=\green{(M_m^{-1})^T \cdot N} N1=(Mm−1)T⋅N
那么结果已经出来了, ( M m − 1 ) T \green{(M_m^{-1})^T} (Mm−1)T 就是我们的 M n M_n Mn 法线矩阵,就是 M m M_m Mm 的 逆矩阵的转置矩阵
(关于逆矩阵怎么求,你也可以查看我之前的一篇学习笔记:LearnGL - 06.2 - Matrix - 矩阵03 - 逆矩阵、行列式、伴随矩阵、余子式、代数余子式、练习)
总结
这些图形学基础中矩阵变换,建议去吭一下,因为后续会有很多各种各样的变换需求,如果这些基础的变换你能学习、理解这些意义,后续就会越学越顺。
虽然这个 法线矩阵 IT_mMat 本质上暂时没找到很好的理解方式,但是知道他是通过这些数学公式,可重新推导出来的就够了。(当然,如果大神的您,对法线矩阵 有很好的、了解本质的教程,希望您能分享一下,感激不尽!)
而且,后面还有一些 世界空间 到 切线空间 的变换,或是 切线空间 到 世界空间 的变换矩阵(这个知识点,我之前学习过,但是这次为了完善 LearnGL 系列的内容,我会重复再详细的讲解一次,当做温习),这些是为了后续的 法线贴图 需要准备的知识点。
References
- 顶点法向量从物体坐标系变换到世界坐标系