SCATTER: Selective Context Attentional Scene Text Recognizer --- 论文阅读笔记
Paper : https://arxiv.org/abs/2003.11288
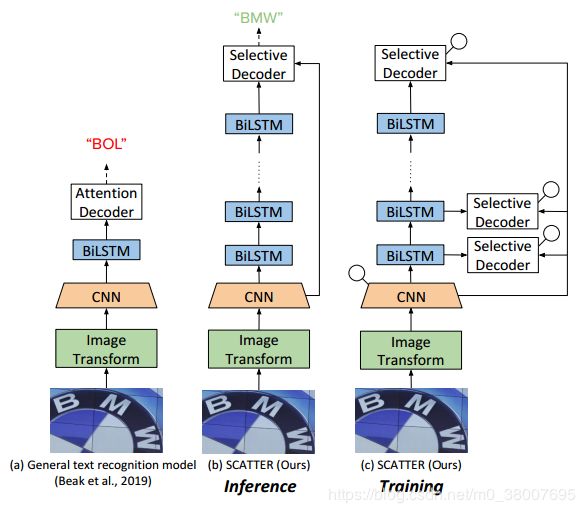
SCATTER 在训练过程中采用了带有中间监督的堆叠式块体系结构,从而为成功训练深度 BiLSTM 编码器铺平了道路,从而改善了上下文相关性的编码。 解码使用两步注意力机制完成。 第一步是对CNN主干的视觉特征以及BiLSTM层计算的上下文特征进行加权。 第二个注意力将这些特征视为一个序列,并加入到序列间的关系中。
Pipeline
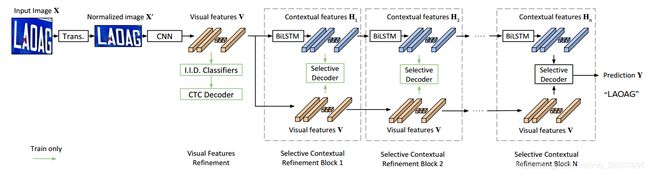
SCATTER 包含四部分,在 Visual Feature Refinement 部分使用 CTC 损失监督训练,在 Selective-Contextual Refinement Block 部分可以使用多个 block 进行解码训练
- Transformation : 使用 TPS 网络对输入图像做矫正
- Feature Extraction : 使用文本注意力模型把输入图像映射为特征表示
- Visual Feature Refinement : 直接监视视觉特征中的每一列。 通过将特征列分类为单独的符号来细化每个特征列中的表示形式
- Selective-Contextual Refinement Block : 每一个 block 包含一个两层的 BILSTM 编码器输出上下文特征。把上下文特征和视觉特征拼接起来,作为 selective-decoder ( 一个两步的 attention 机制 )的输入,
Feature Extraction
使用 ResNet 做图像特征提取,输出特征图 F = [ f 1 , f 2 , . . . , f N ] F=[f_1,f_2,...,f_N] F=[f1,f2,...,fN] ,然后使用 文本注意力模块 输出 N N N 个视觉特征序列 V = [ v 1 , v 2 , . . . , v N ] V=[v_1,v_2,...,v_N] V=[v1,v2,...,vN]
文本注意力模块 ( text attention module )
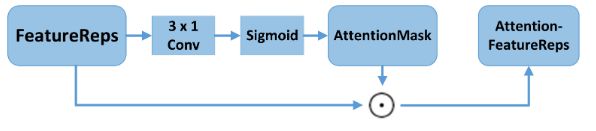
对 F F F 采用 3x1 步长为 1x1 的卷积和 sigmoid 激活函数输出 AttentionMask;然后 F F F 和 AttentionMask 采用逐元素点积操作得到 Attention FeatureReps,然后转换为特征序列 V V V
作用:特征过滤,使用语义信息增强特征列,抑制了冗余和混乱,更加关注文本部分
Visual Feature Refinement
视觉特征序列 V V V 用于中间解码。 中间监督目标是完善 V V V 的每一列中的字符嵌入(表示),并使用基于 CTC 的解码来完成。把 V V V 输入到一个全连接层中,输出长度为 N N N 的序列 H H H。输出序列使用 CTC 解码以生成最终输出。
这部分损失表示为 L C T C L_{CTC} LCTC
Selective-Contextual Refinement Block
使用两层 BiLSTM 编码视觉特征序列 V V V ,输出 H = [ h 1 , h 2 , . . . , h n ] H=[h_1,h_2,...,h_n] H=[h1,h2,...,hn] 。用 D = ( V , H ) D = (V,H) D=(V,H) 表示一个新的特征空间。
特征空间 D D D 既用于 selective decoder,又用作下一个 Selective-Contextual Refinement Block 的输入。第 j j j 个 block 的拼接输出可以写成 D j = ( V , H j ) D_j = (V,H_j) Dj=(V,Hj),下一个 j + 1 j+1 j+1 块使用 H j H_j Hj 作为两层 BiLSTM 的输入,输出 H j + 1 H_{j+1} Hj+1 ,则第 j + 1 j+1 j+1 个特征空间更新为 D j + 1 = ( V , H j + 1 ) D_{j+1} = (V, H_{j+1}) Dj+1=(V,Hj+1) 。视觉特征 V V V 在 Selective-Contextual Refinement Block 块中未进行任何进一步的更新。这些块可以根据所需的任务或精度级别按需要多次堆叠在一起,最终的预测由解码器根据最后一个块提供。
Selective-Decoder
使用两步 attention 机制。
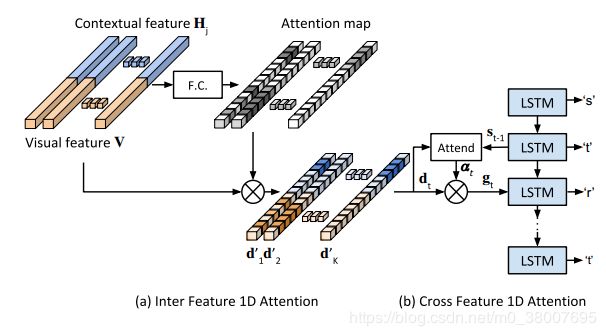
首先,使用 self-attention 对 D D D 进行处理,使用一个全连接层计算特征的 attention map。接下来,计算 attention map 和 D D D 之间的乘积,得出注意特征 D ′ D' D′。 D ′ D' D′ 的解码是通过单独的注意力解码器完成的,因此对于每个 t t t 时间步,解码器输出 y t y_t yt
计算注意力权重:
e t , i = w T tanh ( W s t − 1 + V d i ′ + b ) (1) e_{t,i} = w^T \tanh(Ws_{t-1} + V d_i' + b) \tag{1} et,i=wTtanh(Wst−1+Vdi′+b)(1)
α t , i = exp ( e t , i ) / ∑ i ∗ = 1 n e t , i ∗ (2) \alpha_{t,i} = \exp(e_{t,i}) / \sum_{i^* = 1}^n e_{t,i^*} \tag{2} αt,i=exp(et,i)/i∗=1∑net,i∗(2)
b , w , W , V b, w, W, V b,w,W,V 是训练参数, s t − 1 s_{t-1} st−1 是时间 t − 1 t-1 t−1 的隐藏状态, d ′ d' d′ 是 D ′ D' D′ 的一列 。解码器将 D ′ D' D′ 的列线性组合为向量 G G G
g t = ∑ i = 1 n α t , i d i ′ (3) g_t = \sum_{i=1}^n \alpha_{t,i} d'_i \tag{3} gt=i=1∑nαt,idi′(3)
然后,输入到解码器的 cell 中:
( x t , s t ) = R N N ( s t − 1 , ( g t , f ( y t − 1 ) ) ) (4) (x_t, s_t) = RNN(s_{t-1}, (g_t, f(y_{t-1}))) \tag{4} (xt,st)=RNN(st−1,(gt,f(yt−1)))(4)
其中 ( g t , f ( y t − 1 ) ) (g_t, f(y_{t-1})) (gt,f(yt−1)) 表示 g t g_t gt 和 y t − 1 y_{t-1} yt−1 的 one-hot 编码的拼接。
给定字符 y t y_t yt 的概率:
p ( y t ) = softmax ( W o x t + b o ) (5) p(y_t) = \text{softmax}(W_o x_t + b_o) \tag{5} p(yt)=softmax(Woxt+bo)(5)
第 j j j 个 block 的损失是负对数似然,表示为 L A t t n , j L_{Attn,j} LAttn,j
Training Losses
L = λ C T C ⋅ L C T C + ∑ j = 1 λ j L A t t n , j (6) L = \lambda_{CTC} \cdot L_{CTC} + \sum_{j=1} \lambda_j L_{Attn, j} \tag{6} L=λCTC⋅LCTC+j=1∑λjLAttn,j(6)
λ C T C , λ j \lambda_{CTC}, \lambda_j λCTC,λj 分别设置为 0.1 , 1.0 0.1,1.0 0.1,1.0
Inference
推理阶段,不需要任何的中间解码器,只使用最后一个解码器输出最终结果。
Experiments
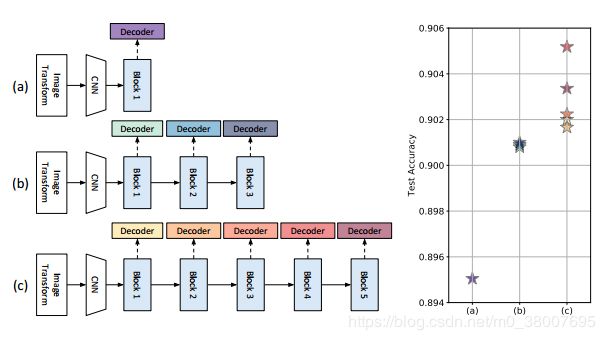
上图展示出了针对不同的堆叠布置在中间辅助解码器处计算的准确等级,从而证明了随着相继添加附加块,性能的提高。 依次训练附加块也可以提高中间解码器的精度(与采用较浅堆叠结构进行训练相比)。可以先训练具有更多块的深度网络然后进行修剪,这样在相同的网络结构的情况下,结果会有所提升。