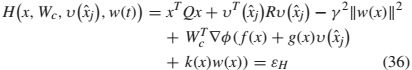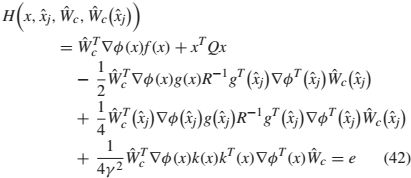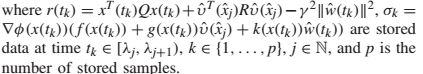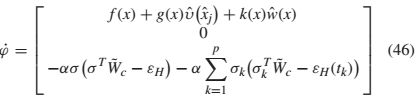Event-Triggered H∞ Control for Continuous-Time Nonlinear System via Concurrent Learning
摘要
本文利用事件触发法研究了一类连续时间非线性系统的H∞最优控制问题。
①首先,H∞最优控制问题被公式化为二人零和(ZS)差分博弈。
②然后,利用事件触发的控制策略和时间触发的干扰策略,为ZS博弈导出自适应触发条件。仅当不满足触发条件时才更新事件触发的控制器。因此,减少了设备与控制器之间的通信。
③此外,提供最小采样时间的正下界以避免Zeno行为。
④为了实现目的,提出了事件触发的并发学习算法,其中仅使用一个评价神经网络(NN)来近似值函数,控制策略和干扰策略。在学习过程中,记录的数据和瞬时数据一起使用,放松了过去的激励条件持久性要求。
⑤同时,利用Lyapunov技术证明了闭环系统的稳定性和NN参数的均匀极限有界性(UUB)。
⑥最后,仿真结果验证了ZS博弈的可行性和相应的H∞控制问题。
1. 介绍
作为一种强大的用于衰减干扰效应的鲁棒控制方法[1],[2],H∞控制在过去几年中受到越来越多的关注[3] - [5]。从最小极大优化问题的角度来看,H∞控制问题可以表述为二人零和(ZS)博弈[6],[7]。为了获得在最坏情况扰动中最小化性能指标的控制器,需要通过求解Hamilton-Jacobi-Isaacs(HJI)方程来找到纳什均衡解。然而,在非线性系统的情况下,给出HJI方程的解析解是难以处理的。
为了求解HJI方程,已经为ZS博弈问题提出了许多方法,包括强化学习(RL),自适应动态规划(ADP)[8] - [14]。对于离散时间(DT)系统,启发式动态规划(HDP)和双启发式动态规划(DHP)被用于线性系统[15],[16]提出了一种Q学习算法来解决GARE,不使用任何系统动力学。魏等人 [17]提出了一种基于数据的迭代自适应评价设计算法,用于未知的Roesser 2-D系统。刘等人 [18]提出了一种用于H∞最优调节和跟踪控制问题的贪婪HDP算法,其中只需要一个迭代循环。在[19]中,提出了一种自适应学习算法来解决具有神经网络(NN)标识符的未知D-T系统的H∞控制问题。 Mehraeen等。 [20]开发了一种离线迭代算法,通过泰勒级数展开来解决HJI方程的解。对于连续时间(C-T)系统,Abu-Khalaf等人 [21],[22]开发了一个策略迭代方案,其中两个迭代循环用于具有输入饱和度的ZS博弈。在[23]和[24]中,积分RL(IRL)分别用于具有部分未知动力学和完全未知动力学的线性ZS博弈。 Vamvoudakis和Lewis [25]提出了一种用于非线性ZS博弈的同步策略迭代算法(SPIA),其中所有NN同时进行调整。在[26]中,该方法被扩展用于约束输入系统的H∞控制。张等人[27]开发了一种迭代ADP方法来解决非线性ZS博弈,其对于可能不存在鞍点的情况是有效的。在[28]中,提出了一种基于Galerkin逼近方法求解H∞控制问题的具有收敛性分析的同时策略更新算法。
应该注意的是,在大多数上述文献中使用了具有固定采样周期的传统时间驱动策略来更新所设计的控制器。由于计算效率方面的能力[29],事件触发控制方法最近引起了学术界的极大兴趣。在事件触发控制方法中,仅当不满足触发条件时,才基于新的采样状态更新控制器。这可以显着减少设备和控制器之间的通信。在[30]和[31]中,采用事件触发策略分别解决了无线传感器网络上的分布式滤波问题和具有随机时变的非线性系统的有限时域H∞故障估计问题。特别地,近年来事件触发的控制方法已经与RL方法集成。在[32]中,基于C-T非线性系统的actor-critic结构,实现了一种最优自适应事件触发控制算法。为了保证系统的稳定性,在闭环系统中增加了一个有争议的量。钟等人 [33]将事件触发控制技术集成到不使用系统动力学的非线性系统的RL方法中。 Sahoo等[34]为C-T网络控制系统开发了事件触发的近似最优控制方案。 NN标识符用于近似未知系统动态。然后,通过使用[35]中的输入输出数据,将这种事件触发的近似最优控制方案扩展到D-T非线性系统。
另一方面,在[36]中提出了一种不确定系统的并发学习技术,它可以使用记录的和可用的数据来放松传统的激发持续性(PE)条件[37]。在[38]中,在NN识别器中采用了一种称为经验重放的相关概念来识别未知的非线性C-T系统。在[39]中,该技术通过收敛性和稳定性分析扩展到约束非线性系统的IRL算法。Yasini 等人 [40],[41]分别开发了在线并发算法来解决具有部分未知系统动力学的ZS博弈和具有输入约束的非线性动力系统的多人非ZS博弈。然后它被扩展到[42]中完全未知的非线性系统的ZS博弈。在[43]中,并发学习被用于N-player非ZS博弈,其中不需要系统漂移动态的确切知识。杨等人[44]开发了一种新颖的actor-critic体系结构,没有初始稳定控制输入,用于解决基于并发学习的不确定非线性系统的近似最优控制问题。
据我们所知,通过并发学习,非线性系统的事件触发H∞最优控制问题没有结果。在本文中,H∞控制问题被转换为ZS微分博弈,其中一个最小化玩家一个最大化玩家。为了减少通信资源,在学习过程中将事件触发的策略引入控制输入。此外,评价NN采用并行学习来放松传统的PE条件。最后,一个在线事件触发的并发学习(ETCL)算法与一个评价NN结构一起呈现。
主要贡献分三部分。
1)通过事件触发控制机制,首次建立了具有未知扰动的非线性系统的H∞最优控制方案。此外,导出触发条件以保证相应ZS博弈的稳定性。
2)对芝诺行为的分析是为了保证在最小的采样时间内存在较低的正有界。此外,可以放松传统PE条件的并发学习技术用于调整评价NN的权重。
3)提出了ETCL算法。开发了一种新的评价NNs权重调整法,并推导出一种自适应触发条件,可以保证NNs参数的收敛性和闭环系统的稳定性。
本文的其余部分安排如下。我们首先介绍了H∞控制的问题公式和事件触发控制的机制。在第III节中,事件触发的H∞控制问题被描述为ZS博弈并且导出触发条件。在第四节中,提出在线ETCL算法以通过稳定性分析来近似最优控制策略。最后是我们的模拟结果和结论。
IV 在线神经优化控制方案
在本节中,提出了在线ETCL算法。与[20]中的actor-critic-disturbanceNN结构相比,该方案中只需要一个critic NN。在并行学习技术的基础上,给出了一个新的critic NN权重调整规则,给出了一个宽松的PE条件。然后相应地更新时间触发的干扰策略,并且在由触发条件确定的采样时刻{λj}∞j= 0处更新事件触发的控制策略。通过使用ZOH,控制律序列被转换为C-T控制信号。
A. ETCL算法
根据Weierstrass高阶近似定理[46],基于NN的值函数可以写成
![]()
其中Wc∈RN和φ(x)∈RN是critic NN理想权值和激活函数向量,N是隐藏神经元的数量,ε∈R是critic NN近似误差。
(34)关于x的导数可以由下式给出
![]()
使用NN值函数近似,考虑事件触发控制策略![]() 和时间触发干扰策略w(x),ZS Bellman方程可以写成
和时间触发干扰策略w(x),ZS Bellman方程可以写成
![]()
在关于系统动力学的Lipschitz假设下,剩余误差在局部有界。在[25]中显示,随着隐层单元的数量增加,该误差均匀地收敛到零。也就是说,存在![]() ,使得
,使得![]() 。
。
设![]() 是critic NN的未知理想权重向量Wc的估计。critic NN的实际输出可以表示为
是critic NN的未知理想权重向量Wc的估计。critic NN的实际输出可以表示为
![]()
因此,时间触发的干扰策略(12)和事件触发的控制策略(14)可以近似为
![]() 是在触发时刻λj的理想权重Wc的基于事件的估计。然后闭环系统动力学(3)现在可以改写为
是在触发时刻λj的理想权重Wc的基于事件的估计。然后闭环系统动力学(3)现在可以改写为
![]()
近似的哈密顿函数是
基于并发学习技术,可以通过与当前数据同时记录的数据来更新critic NN权重。在时间tk定义残差方程误差为
![]()
条件1:设![]() 是对应于评论家NN权重的记录数据。那么M包含与对应的评论NN的隐藏神经元的数量一样多的线性独立元素,即秩(M)= N.
是对应于评论家NN权重的记录数据。那么M包含与对应的评论NN的隐藏神经元的数量一样多的线性独立元素,即秩(M)= N.
为了导出e的最小值,希望选择Wc以最小化相应的平方残差![]() 。定义
。定义![]() 。考虑到同时学习,我们为critic NN制定了一个新的权重调整法
。考虑到同时学习,我们为critic NN制定了一个新的权重调整法
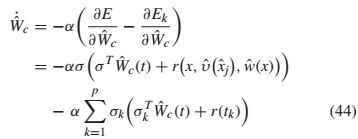
其中![]() ,σk在(43)中定义,
,σk在(43)中定义,![]() 表示存储数据点的索引,α> 0表示学习速率。
表示存储数据点的索引,α> 0表示学习速率。
备注6:本文提出的在线算法不依赖于难以在线检查的传统PE条件。根据[44],(44)中的第二项可以用于放松条件1的PE条件。感兴趣的读者可以在那里获得更多细节。值得一提的是,条件1可以在线轻松检查[36]。
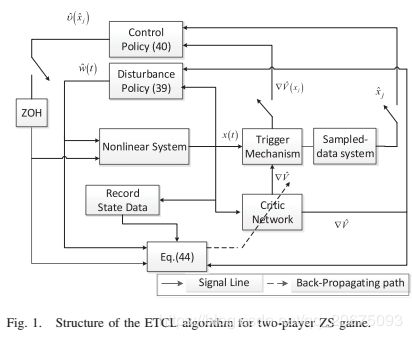
到目前为止,我们有了更新评价网络的规则。然后我们给出了图1中二人ZS游戏的在线ETCL算法的结构。注意,基于时间驱动策略更新评价网络和干扰策略,同时基于事件触发机制更新控制策略。
通过将critic NN的权重估计误差定义为![]() 并且采用时间导数
并且采用时间导数
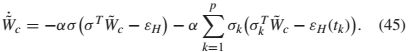
由于控制器仅在事件触发时刻更新,因此系统应被视为脉冲系统。定义增强状态:![]() .在获得
.在获得![]() 的时间导数后,我们得到了
的时间导数后,我们得到了
五 模拟
在本节中,给出了两个仿真示例来演示ETCL算法的有效性。
A. 二人线性零和博弈
考虑一下C-T F16平台[40]
![]()
其中
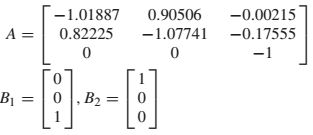
系统状态向量是![]() ,其中表示迎角,q是俯仰率,δe是升降舵偏转角。控制输入u表示升降舵致动器电压,并且干扰w是阵风进入迎角。设Q和R为具有近似维数的单位矩阵,
,其中表示迎角,q是俯仰率,δe是升降舵偏转角。控制输入u表示升降舵致动器电压,并且干扰w是阵风进入迎角。设Q和R为具有近似维数的单位矩阵,![]()
对于线性系统,HJI方程的解通过Riccati方程的解给出。根据[40],最优矩阵P是

选择critic NN激活函数为φ(x)=![]() 。因此,NN权重的理想值是
。因此,NN权重的理想值是
![]()
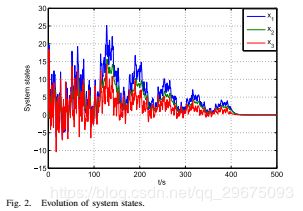
初始状态选择为![]() ,学习速率选择为α= 18.触发条件的参数选择为L = 3.critic NN中的记录数据向量选择10阶,即p = 10.在学习过程中,探测噪声被添加到控制输入并且扰动前400秒。在探测噪声关闭后,系统状态收敛为零,图2显示了系统状态的演变。图3显示了评价参数的收敛性。在100 s之后,评价参数收敛到Wc=
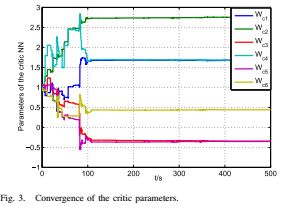
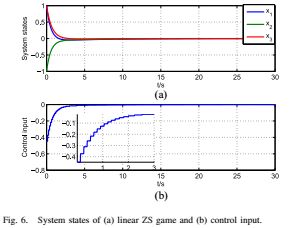
,学习速率选择为α= 18.触发条件的参数选择为L = 3.critic NN中的记录数据向量选择10阶,即p = 10.在学习过程中,探测噪声被添加到控制输入并且扰动前400秒。在探测噪声关闭后,系统状态收敛为零,图2显示了系统状态的演变。图3显示了评价参数的收敛性。在100 s之后,评价参数收敛到Wc=![]() ,这几乎是上面的理想值。在图4中,可以看到事件触发的误差收敛到零,因为状态收敛到零。图5中提供了控制策略的事件触发学习过程期间的采样周期。特别是,事件触发控制器使用543个状态样本,而时间触发控制器使用50 000个样本,这意味着事件 - 触发方法改善了学习过程。然后我们使用获得的最优控制策略和干扰策略来进行具有触发条件的线性ZS博弈(18)。图6显示ZS博弈的系统状态可以收敛到均衡,并且控制输入随事件调整。
,这几乎是上面的理想值。在图4中,可以看到事件触发的误差收敛到零,因为状态收敛到零。图5中提供了控制策略的事件触发学习过程期间的采样周期。特别是,事件触发控制器使用543个状态样本,而时间触发控制器使用50 000个样本,这意味着事件 - 触发方法改善了学习过程。然后我们使用获得的最优控制策略和干扰策略来进行具有触发条件的线性ZS博弈(18)。图6显示ZS博弈的系统状态可以收敛到均衡,并且控制输入随事件调整。
选择t0 = 5的干扰信号然后,我们使用基于收敛评论参数的控制器(11)用于具有干扰的闭环系统(62)。图7显示了系统状态和控制输入。
B.双人非线性零和博弈
考虑一个非线性系统[40]
![]()
其中

设Q和R为近似维数的单位矩阵,γ= 4,x0 = [1,-1] T,α= 20.触发条件的参数选择为L = 5.评价中记录的日期向量NN选择为p = 15.探测噪声被添加到控制输入并且扰动前270秒。图8示出了在关闭探测噪声之后系统状态收敛到零。评价参数的收敛如图9所示。我们可以看到critic NN的参数收敛于Wc [0.5072 0.0501 1.0819 0.0351 0.0109]。从图10中,可以得到事件触发的误差ej(t),并且当状态收敛到零时,阈值eT收敛到零。此外,当不满足触发条件时,事件触发的错误被强制为零,即在触发瞬间对系统状态进行采样。图11中提供了控制策略的事件触发学习过程期间的采样周期。特别是,事件触发控制器使用1835个状态样本,而时间触发控制器使用35000个样本,这意味着由于事件触发的采样,工厂和控制器之间需要更少的传输。这将显着降低通信成本。然后,我们使用获得的最优控制策略和扰动策略来进行具有触发条件的非线性ZS博弈(18)。图12显示了具有事件触发控制输入的非线性ZS博弈的状态轨迹。
然后,我们将基于收敛的评价参数的控制器(11)应用于具有干扰信号的非线性系统(62)。从图13(a)可以看出,闭环系统是渐近稳定的。为了显示ETCL方法的有效性,我们将ETCL方法获得的结果与[40]中的并发RL算法(CRLA)和[25]中的SPIA进行了比较。控制输入如图13(b)所示。可以注意到,基于ETCL方法的最优控制器响应于干扰信号具有更好的性能。