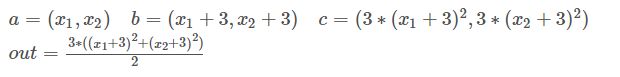torch grad梯度 requires_grad zero_grad backward过程及使用例子
总体过程
对于epoch训练开始之前,经历数据加载、模型定义、权重初始化、优化器定义
netG=netG = net.dehaze(inputChannelSize, outputChannelSize, ngf)
netG.apply(weights_init)
if opt.netG != '':
netG.load_state_dict(torch.load(opt.netG),strict=False)
optimizerG = optim.Adam(netG.parameters(), lr = opt.lrG, betas = (opt.beta1, 0.999), weight_decay=0.00005)
对于每个epoch中的batch大都进行下述操作:
### 梯度可导
for p in netD.parameters():
p.requires_grad = True
### forward + backward
outputs = netD(inputs)
loss = criterion(outputs, labels)
### optimize
# zero the parameter gradients
optimizer.zero_grad() #等效netD.zero_grad()
loss.backward()
optimizer.step() # update parameters
权重更新需注意
第一个地方:
requires_grad
#coding=utf-8
# 如果调用backward的时候,所有的变量都是不可导的,那么最后会报出没有可到变量的错误
import torch
from torch import autograd
input=torch.FloatTensor([1,2,3])
input_v=autograd.Variable(input,requires_grad=False)#False改为true才可行,不加requires_grad默认为false
loss=torch.mean(input_v)
print (loss.requires_grad)
loss.backward()
print( input_v)
print (input_v.grad)
- 对于继承自 nn.Module 的某一网络 net 或网络层,定义好后,发现 默认情况下,net.paramters 的 requires_grad 就是 True 的,这跟普通的Variable张量不同。因此,当x.requires_grad == False , y = net(x) 后, 有 y.requires_grad == True ;
- 但值得注意,虽然nn.xxloss和激活层函数,是继承nn.Module的,但是这两种并没有网络参数,就更谈不上 paramters.requires_grad 的值了。所以类似这两种函数的输出,其requires_grad只跟输入有关,不一定是 True .
第二个地方:
.zero_grad()
根据pytorch中的backward()函数的计算,当网络参量进行反馈时,梯度是被积累的而不是被替换掉;但是在每一个batch时毫无疑问并不需要将两个batch的梯度混合起来累积,因此这里就需要每个batch设置一遍zero_grad 了。
当optimizer=optim.Optimizer(model.parameters())时,两者等效
model.zero_grad()
optimizer.zero_grad()
backward()
梯度求解。
eg
# simple gradient
a = v(t.FloatTensor([2, 3]), requires_grad=True)
b = a + 3
c = b * b * 3
out = c.mean()
out.backward()
print('*'*10)
print('=====simple gradient======')
print('input')
print(a.data)
print('compute result is')
print(out.item())
print('input gradients are')
print(a.grad.data)#输出梯度
out
=====simple gradient======
input
tensor([2., 3.])
compute result is
91.5
input gradients are
tensor([15., 18.])
对a 求偏导:
![]()
可以看到执行backward后,tensor 的 .grad数据更新
参数
相关标志位/函数
1
requires_grad
volatile
detach()/detach_()
2
retain_graph
retain_variables
create_graph
前三个标志位中,最关键的就是 requires_grad,另外两个都可以转化为 requires_grad 来理解。
后三个标志位,与计算图的保持与建立有关系。
其中 retain_variables 与 retain_graph等价,retain_variables 在pytorch0.4+ 新版本中被取消掉。
当需要两次backward时候,改参数
out.backward(retain_graph=True)
每次 backward() 时,默认会把整个计算图free掉。一般情况下是每次迭代,只需一次 forward() 和一次 backward() ,前向运算forward() 和反向传播backward()是成对存在的,一般一次backward()也是够用的。但是不排除,由于自定义loss等的复杂性,需要一次forward(),多个不同loss的backward()来累积同一个网络的grad,来更新参数。于是,若在当前backward()后,不执行forward() 而可以执行另一个backward(),需要在当前backward()时,指定保留计算图,即backward(retain_graph)
注意:只有标量才能直接使用 backward(),即loss.backward() , pytorch 框架中的各种nn.xxLoss(),得出的都是minibatch 中各结果 平均/求和 后的值。如果使用自定义的函数,得到的不是标量,则backward()时需要传入 grad_variable 参数,这一点详见博客 https://sherlockliao.github.io/2017/07/10/backward/ 。
对于自己的非标量,第一个传入 偏导系数 即可:
对于一维向量:
m=(x1,x2)=(2,3),n=(x12,x23)
m = Variable(torch.FloatTensor([[2, 3]]), requires_grad=True)
n = Variable(torch.zeros(1, 2))
n[0, 0] = m[0, 0] ** 2
n[0, 1] = m[0, 1] ** 3
n.backward(torch.FloatTensor([[1, 1]]),retain_graph=True)########既有两次求导,又需要设置[1,1]的系数,具体体现在下面二维可以看出
print(m.grad)
print(m.grad)
tensor([[ 4., 27.]])
对于高维向量:
求jacobian矩阵,
![]()
# jacobian
j = t.zeros(2 ,2)
k = v(t.zeros(1, 2))
m.grad.data.zero_()
k[0, 0] = m[0, 0] ** 2 + 3 * m[0 ,1]
k[0, 1] = m[0, 1] ** 2 + 2 * m[0, 0]
k.backward(t.FloatTensor([[1, 0]]), retain_variables=True)###只获取对x1的偏导
j[:, 0] = m.grad.data
m.grad.data.zero_()
k.backward(t.FloatTensor([[0, 1]]))###只获取对x2的偏导
j[:, 1] = m.grad.data
print('jacobian matrix is')
print(j)
out:
jacobian matrix is
tensor([[4., 2.],
[3., 6.]])
更新 .step()
- 一些特殊的情况:
固定特定网络:
for p in sub_module.parameters():
p.requires_grad = False
ref
https://blog.csdn.net/douhaoexia/article/details/78821428