2020杭电多校第二场部分题解(1001, 1005, 1006, 1007, 1009, 1010, 1012)

1001 Total Eclipse

题意：给一个n点m边的图，每个点有点权。每次可以选择一个点权全是正数的点组成的连通块，让它们的权值整体-1.问让全部的点权变为0需要多少次操作.$(1\le n,m\le 1e5)$
（一开始题目意思其实是任选若干个点组成的连通块，后来出题人发现不对劲就改成这样的题意了）

解题思路：对于一个连通块来说，可以一直操作 $min(a_i)$次（$a_i$是连通块内权值最小的那个点)，然后最小的那些点就会变成0，此时可能会让连通块分裂成多个连通块。这种删除边得到多个连通块的情况不好处理，可以反过来想：处理添加边把连通块融合的情况。那就从最大的点开始倒着添加边。一开始加入新的点，它作为单独的个体$i$，所以要操作$a_i$次，然后把它的边依次加上。如果加了这个边使得两个连通块融合，那么这两个连通块里面的点权都是大于等于$a_i$的，所以它们可以共享这$a_i$次操作，所以省去了$a_i$次操作，答案-$a_i$。

#include
#define ll long long
#define pb push_back
#define lowbit(x) ((x)&(-(x)))
#define mid ((l+r)>>1)
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define fors(i, a, b) for(int i = (a); i < (b); ++i)
#define P pair
using namespace std;
const int maxn = 1e5 + 5;
vector<int> g[maxn];
int fa[maxn];
P a[maxn];
int n, m;
int vis[maxn];
int fnd(int x){
    if(fa[x] == x) return x;
    return fa[x] = fnd(fa[x]);
}
void link(int x, int y){
    int rx = fnd(x), ry = fnd(y);
    if(rx != ry) fa[rx] = ry;
    return;
}
void init(){
    scanf("%d%d", &n, &m);
    fors(i, 1, n+1) scanf("%d", &a[i].first),a[i].second = i, g[i].clear(), fa[i] = i, vis[i] = 0;
    while(m--){
        int u, v; scanf("%d%d", &u, &v);
        g[u].pb(v); g[v].pb(u);
    }
}
void sol(){
    sort(a+1,a+1+n);
    ll ans = 0;
    for(int i = n; i > 0; --i){
        ans += a[i].first;
        int u = a[i].second;
        for(int v: g[u]){
            if(!vis[v]) continue;
            int rt = fnd(v);
            if(fnd(u) != rt) {
                link(u, v); ans -= a[i].first;
            }
        }
        vis[u] = 1;
    }
    printf("%lld\n", ans);
}
int main()
{
    int T; cin>>T;
    while(T--){
        init();
        sol();
    }
}

1005 New Equipments

题意：n个工人，m个机器，第$i$个工人和第$j$个机器匹配的权值是$a_i{j}^2+b_{i}j+c_i$，问取k个两个配对工人机器的最小权值是多少。k取1,2,…n。一个工人只能匹配一个机器，一个机器只能匹配一个工人。($1\le n\le 50,n\le m\le 1e8)$

解题思路: 最大权匹配问题，如果n和m都比较小可以使用费用流来解决这个问题，每增广一次输出答案即可。但是m很大，有1e8级别。但是观察权值我们可以发现这是一个二次函数，对于特定的工人很容易找到让这个权值最小的j。那我们在这个点附近取n个点，这个工人匹配的机器一定在这n个点之中。那么我们就有了一张$n+n^2+2$个点，$n\ast n+2n$条边的网络流图。跑费用流就可以了。
一点优化：其实对于单个工人，它的最优点最多就两个，把这些点作为区间取出来，然后每有重叠的区间就进行合并并且把区间扩展2个点，这样可以保证区间内的点一定包含最优解需要点。这样每合并一次区间扩展两个点，最多扩展50次，一开始最多100个，得到了最多有250个点的网络流图。不过边数还是$n^2$级别的。

#include
#define ll long long
#define pb push_back
#define lowbit(x) ((x)&(-(x)))
#define mid ((l+r)>>1)
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define fors(i, a, b) for(int i = (a); i < (b); ++i)
using namespace std;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int maxn = 255;
struct node{
	int u,v,f,nxt;
	ll w;
}e[maxn*maxn];
int cnt = 0;
int head[maxn];
void add(int u,int v,int f,ll w){
	e[cnt].u = u;
	e[cnt].v = v;
	e[cnt].f = f;
	e[cnt].w = w;
	e[cnt].nxt = head[u];
	head[u] = cnt++;

	e[cnt].u = v;
	e[cnt].v = u;
	e[cnt].f = 0;
	e[cnt].w = -w;
	e[cnt].nxt = head[v];
	head[v] = cnt++;
}
int n,m;
int st,ed,ex;
int pre[maxn];
int inq[maxn];
int flow[maxn];
ll dis[maxn];
ll spfa(){
	memset(dis,0x3f,ex<<3);
	memset(pre,-1,ex<<2);
	memset(inq,0,ex<<2);
	queue<int> q;q.push(st);
	dis[st] = 0;inq[st] = 1;
	flow[st] = 0x3f3f3f3f;
	while(q.size()){
		int u = q.front();q.pop();inq[u] = 0;
		for(int i = head[u];i!=-1;i = e[i].nxt){
			int v = e[i].v;
			if(e[i].f && dis[v] > dis[u] + e[i].w){
				dis[v] = dis[u] + e[i].w;
				pre[v] = i;
				flow[v] = min(flow[u],e[i].f);
				if(!inq[v]) inq[v] = 1,q.push(v);
			}
		}
	}

	if(pre[ed] == -1) return -1;
	return flow[ed];
}
ll mfmv(){
	ll ans = 0;
	int d;
	int flag = 0;
	while((d = spfa())!=-1){
		ans += d*dis[ed];
		int v = ed;
		while(v!=st){
			e[pre[v]].f-=d;
			e[pre[v]^1].f+=d;
			v = e[pre[v]].u;
		}
		if(flag) printf(" ");
		printf("%lld", ans);
		flag = 1;
	}printf("\n");
	return ans;
}
ll a[55], b[55], c[55];
#define P pair
vector<P> Q;
P ready[55];
int tot = 0;
int mark[255], sz = 0;
void init(){//设置原点和终点and点数,连边
	cnt = 0;
	memset(head,-1,sizeof head);
	scanf("%d%d", &n, &m);
	fors(i, 1, n+1) scanf("%lld%lld%lld", &a[i], &b[i], &c[i]);
	st = 0;
	Q.clear();
	fors(i, 1, n+1){
        if(b[i] >= 0) Q.pb(P(1,2));
        else{
            int t1 = -b[i]/(2*a[i]);
            int t2 = t1+1;
            if(t1 == 0) t1 = 1, t2 = 2;
            else if(t1 >= m) t1 = m-1, t2 = m;
            Q.pb(P(t1,t2));
        }
	}
	sort(Q.begin(), Q.end());
	tot = 0; ready[tot++] = Q[0];
	fors(i,1,Q.size()){
        P t = Q[i];
        while(tot > 0 && t.first <= ready[tot-1].second){
            t.first = min(t.first, ready[tot-1].first);
            t.second = max(t.second, ready[tot-1].second);
            if(t.first == 1){
                fors(x, 0 , 2){
                    if(t.second+1 <= m) t.second++;
                }
            }else if(t.second == m){
                fors(x, 0 , 2){
                    if(t.first-1 >= 1) t.first--;
                }
            }else{
                t.first--; t.second++;
            }
            tot--;
        }
        ready[tot++] = t;
	}
	sz = 0;
	fors(i, 0, tot){
	    //cout<<"l:"<
        fors(x, ready[i].first, ready[i].second+1){
            mark[++sz] = x;
        }
	}
	ed = n + sz + 1;
	ex = ed+1;
    fors(i, 1, n+1) {
        add(st, i, 1, 0);
        fors(j, 1, sz+1){
            ll w = a[i]*(ll)mark[j]*(ll)mark[j] + b[i]*(ll)mark[j]+c[i];
            add(i, n+j, 1, w);
            //cout<<"w:"<
        }
    }
    fors(j, 1, sz+1){
        add(n+j, ed, 1, 0);
    }
}
void sol(){
    mfmv();
}
int main(){
    int T; scanf("%d", &T);
	while(T--){
		init();
		sol();
	}
}

1006 The Oculus

题意:给出A，B，C的斐波那契数列表达式，C = A*B。其中C的表达式的1位1被抹成了0, 问你是哪一位。
解题思路: 说出来你可能不信，直接算然后每一位依次判断过去就好。什么？溢出？没问题，A * B的结果不需要正确，只需要和C+fib(ans)相等就好。
附上队友的代码

#include
#define LL long long
#define ULL unsigned long long
using namespace std;
const int maxn = 1e6 + 50;
//int a[maxn],b[maxn],c[maxn<<1],n;
int n;
ULL fab[maxn<<1];
int s[maxn<<1];
void f(ULL &a)
{
    int t;
    scanf("%d",&n);
    for(int i=1;i<=n;++i)
    {
        scanf("%d",&t);
        if(t) a+=fab[i];
    }
}
int main()
{
    int T;
    scanf("%d",&T);
    fab[0]=fab[1]=1;
    for(int i=2;i<=2e6+10;++i) fab[i]=fab[i-1]+fab[i-2];
    while(T--)
    {
        ULL a=0,b=0,c=0;
        f(a);f(b);
        scanf("%d",&n);
        for(int i=1;i<=n;++i)
        {
            scanf("%d",s+i);
            if(s[i]) c+=fab[i];
        }
        a*=b;
        //cout<
        for(int i=1;i<n;++i)
        {
            if(s[i]==0)
            {
                s[i]=1;
                if(s[i]*s[i-1]||s[i]*s[i+1]) {s[i]=0;continue;}
                ULL t=c+fab[i];
                //cout<
                if(t==a) {printf("%d\n",i);break;}
                s[i]=0;
            }
        }
    }
    return 0;
}

1007 In Search of Gold

题意：给n($\le 2e4$)点的树，每条边有$a_i,b_i$两种权值，给一个数字$k(\le 20)$，必须选择k条边的权值是类型a，其他边权值是类型b的。问树的直径最小可以是多少。

解题思路：对答案进行二分。然后$dp(i,j)$表示以i为根的子树选择了j条边为a边，向下最远的距离最小可以是$dp(i,j)$，然后每次把儿子的子树加入到当前树的时候判断一下当前树向下的最大距离的最小值+边长+该儿子向下的最大距离的最小值是不是满足二分的限制条件，满足的条件下才能进行转移。如果一路顺利的求到了根节点1，并且$dp(1,k)$是有合法值的，那么我们在dp的过程中所有的可能的直径长度都不超过mid，二分答案的判断就是正确，否则说明中间出现了我不产生大于mid的路径就无法合并子树的情况。
这种合并子树的复杂度比较玄学，先$O(k)$合并第一个儿子的信息，后面的合并中加一个$j\le min(sz[u],k])$的限制条件则每次dp的复杂度是$O(nk)$的。具体证明貌似得看论文。总的复杂度$O(nk)log(ans)$

#include
#define ll long long
#define pb push_back
#define lowbit(x) ((x)&(-(x)))
#define mid ((l+r)>>1)
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define fors(i, a, b) for(int i = (a); i < (b); ++i)
using namespace std;
const int maxn = 2e4 + 50;
const ll inf = 0x3f3f3f3f3f3f3f3f;
struct node{
    int v,a,b;
};
int n, k;
vector<node> g[maxn];
ll dp[maxn][22];
void init(){
    scanf("%d%d", &n, &k);
    fors(i, 0, n+1) g[i].clear();
    fors(i,1,n){
        int u, v, a, b;
        scanf("%d%d%d%d", &u, &v, &a, &b);
        g[u].pb((node){v,a,b});
        g[v].pb((node){u,a,b});
    }
}
ll tmp[21];
int sz[maxn];
void get_sz(int u, int f){
    sz[u] = 0;
    for(node t: g[u]){
        int v = t.v;
        if(v!=f) get_sz(v, u), sz[u] += sz[v]+1;
    }
}
void dfs(int u, int f, ll lim){
    dp[u][0] = 0;
    int first = 1;
    for(node t: g[u]){
        int v = t.v;
        int a = t.a, b = t.b;
        if(v == f) continue;
        dfs(v, u, lim);
        if(first){
            first = 0;
            if(dp[v][0]+b <= lim) dp[u][0] = dp[v][0] + b;
            else dp[u][0] = inf;
            fors(j, 1, min(sz[u], k)+1){
                dp[u][j] = min(dp[v][j]+b, dp[v][j-1]+a);
                if(dp[u][j] > lim) dp[u][j] = inf;
            }
            continue;
        }
        fors(i, 0, k+1) tmp[i] = inf;
        for(int num = 0; num <= min(k, sz[u]); ++num){
            for(int j = 0; j <= num; ++j){
                if(dp[u][j]+b+dp[v][num-j] <= lim) {
                    tmp[num] = min(tmp[num], max(dp[u][j], dp[v][num-j] + b) );
                }
                if(j < num && dp[u][j] + a + dp[v][num-j-1] <= lim){
                    tmp[num] = min(tmp[num], max(dp[u][j], dp[v][num-j-1] + a) );
                }
            }
        }
        fors(i, 0, k+1) dp[u][i] = tmp[i];
    }
}
bool check(ll lim){
    fors(i, 0, n+1) fors(j, 0, k+1) dp[i][j] = inf;
    dfs(1, 1, lim);
    if(dp[1][k] < inf) return true;
    return false;
}
void sol(){
    get_sz(1,1);
    ll l = 1, r = 1e14;
    ll ans = 0;
    while(l <= r){
        if(check(mid)) ans = mid, r = mid-1;
        else l = mid+1;
    }
    printf("%lld\n", ans);
}
int main()
{

    int T; cin>>T;
    while(T--){
        init();
        sol();
    }
}
/*
10 5
1 2 1 1
2 3 1 1
3 4 1 1
4 5 1 1
1 6 1 1
1 7 1 1
3 8 1 1
3 9 1 1
6 10 1 1
*/

1009 It’s All Squares

题意：n*m的棋盘，每个格子上有权值$w_{i,j}$，q次询问，每次给出起点，在边线上 上下左右的走出一个简单多边形，问多边形内部有多少个不同的权值。
解题思路：每次向右走就把这条线下面所有格子对应的权值的cnt值-1，向左走就把这条线下面所有格子对应的权值的cnt值+1，这样最后如果一个格子对应的权值的cnt值不是0的话，它上面必然有奇数根线，则它一定在多边形内部。
(其实最后要么cnt全都小于等于0，要么全部大于等于0，不会有一部分正一部分负的情况）
每走一步需要操作最多400次，所以复杂度$O(\sum |S|\ast n)$

#include
#define ll long long
#define pb push_back
#define lowbit(x) ((x)&(-(x)))
#define mid ((l+r)>>1)
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define fors(i, a, b) for(int i = (a); i < (b); ++i)
using namespace std;
int n, m, q;
int w[404][404];
int cnt[404*404];
int ans;
void init(){
    scanf("%d%d%d", &n, &m, &q);
    fors(i,1,n+1)fors(j,1,m+1) scanf("%d", &w[i][j]);
}
const int maxn = 4e6 + 50;
char cmd[maxn];
vector<int> C;
void sol(){
    C.clear();
    while(q--){
        ans = 0;
        int x, y; scanf("%d%d", &x, &y);
        scanf("%s", cmd);
        char *s = cmd;
        while(*s){
            if(*s == 'R'){
                fors(i, 1, y+1){
                   cnt[w[x+1][i]]++;
                   if(cnt[w[x+1][i]] == 1) ans++, C.pb(w[x+1][i]);
                   else if(cnt[w[x+1][i]] == 0) ans--;
                }
                x++;
            }
            else if(*s == 'L'){
                fors(i, 1, y+1){
                    cnt[w[x][i]]--;
                    if(cnt[w[x][i]] == -1) ans++, C.pb(w[x][i]);
                    else if(cnt[w[x][i]] == 0) ans--;
                }
                x--;
            }else if(*s == 'U') y++;
            else if(*s == 'D') y--;
            s++;
        }
        for(int v: C) cnt[v] = 0;
        C.clear();
        printf("%d\n", ans);
    }
}
int main()
{
    int T; cin>>T;
    while(T--){
        init(); sol();
    }
}

1010 Lead of Wisdom

题意：n个装备k种种类，每个种类装备只能装一个，每个装备有abcd四个属性，总属性是

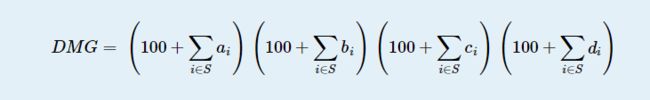
S是装上的装备
问DMG最大可以是多少。
解题思路：暴力搜索，可以特判装备数量<=1的装备。

#include
#define ll long long
#define pb push_back
#define lowbit(x) ((x)&(-(x)))
#define mid ((l+r)>>1)
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define fors(i, a, b) for(int i = (a); i < (b); ++i)
using namespace std;
int n, k;
struct node{int a,b,c,d;};
int vis[55];
vector<node> g[55];
void init(){
    scanf("%d%d", &n, &k);
    fors(i, 0, k+1) g[i].clear(), vis[i] = 0;
    fors(i,0,n){
        int t,a,b,c,d;
        scanf("%d%d%d%d%d", &t, &a, &b, &c, &d);
        vis[t]++;
        g[t].pb((node){a,b,c,d});
    }
}
int tot = 0;
int q[55];
int A, B, C, D;
ll ans;
void dfs(int p){
    if(p == tot){
        ans = max(ans, (ll)A*B*(ll)C*D);
        return;
    }
    for(node t: g[q[p]]){
        A += t.a; B += t.b; C += t.c; D += t.d;
        dfs(p+1);
        A -= t.a; B -= t.b; C -= t.c; D -= t.d;
    }return;
}
void sol(){
    A = B = C = D = 100;
    ans = A*B*C*D;//ans 初始化
    tot = 0;
    fors(i, 1, k+1){
        if(vis[i] == 1) {
            node t = g[i][0];
            A += t.a;
            B += t.b;
            C += t.c;
            D += t.d;
        }else if(vis[i] > 1){
            q[tot++] = i;
        }
    }
    dfs(0);
    printf("%lld\n", ans);
}
int main()
{
    int T; cin>>T;
    while(T--){
        init();
        sol();
    }
}

1012 String Distance

题意：给出字符串a,b，q次查询l,r, 求a[l…r]和b的最长公共子序列长度。b的长度$\le 20$，a的长度$\le 1e5$
解题思路：
nxt[i][j]表示a[i…n]中第一个字母j出现的位置。
$dp(i,j)$表示b的前i个字母匹配了j个，其中最后一个字母和$a[dp(i,j)]$匹配。
那$dp(i,j)$由$dp(i-1,j)和dp(i-1,j-1)$转移，前者代表b[i]不匹配，后者代表b[i]匹配。
每次查询的时候，dp[0][0] = l-1
每次查询进行这样m^2的dp，然后查询最大的使得$dp(m,j)$小于等于$r$的$j$就是公共子序列长度
答案是区间长度+m-2*公共子序列长度

#include
#define ll long long
#define pb push_back
#define lowbit(x) ((x)&(-(x)))
#define mid ((l+r)>>1)
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define fors(i, a, b) for(int i = (a); i < (b); ++i)
using namespace std;
const int maxn = 1e5 + 50;
char a[maxn], b[25];
int n, m;
int nxt[maxn][27];
void init(){
    scanf("%s", a+1); n = strlen(a+1);
    scanf("%s", b+1); m = strlen(b+1);
    fors(i, 0, 26) nxt[n+2][i] = nxt[n+1][i] = n+1;
    for(int i = n; i > 0; --i){
        fors(j, 0, 26) nxt[i][j] = nxt[i+1][j];
        nxt[i][a[i]-'a'] = i;
    }
}
int dp[22][22];
void sol(){
    int q;scanf("%d", &q);
    while(q--){
        int l, r; scanf("%d%d", &l, &r);
        dp[0][0] = l-1;
        int mx = 0;
        fors(i, 1, m+1){
            dp[i][0] = l-1;
            fors(j, 1, i+1){
                if(j <= i-1) dp[i][j] = min(dp[i-1][j], nxt[dp[i-1][j-1]+1][b[i]-'a'] );
                else dp[i][j] = nxt[dp[i-1][j-1]+1][b[i]-'a'];
                if(i == m && dp[i][j] <= r) mx = max(mx, j);
            }
        }
        int ans = (r-l+1+m-mx*2);
        printf("%d\n", ans);
    }
}
int main()
{
    int T; cin>>T;
    while(T--){
        init();
        sol();
    }
}