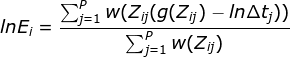Recovering High Dynamic Range Radiance Maps from Photographs

Abstract

We present a method of recovering high dynamic range radiance maps from photographs taken with conventional imaging equipment. In our method, multiple photographs of the scene are taken with different amounts of exposure. Our algorithm uses these differently exposed photographs to recover the response function of the imaging process, up to factor of scale, using the assumption of reciprocity. With the known response function, the algorithm can fuse the multiple photographs into a single, high dynamic range radiance map whose pixel values are proportional to the true radiance values in the scene. We demonstrate our method on images acquired with both photochemical and digital imaging processes. We discuss how this work is applicable in many areas of computer graphics involving digitized photographs, including image-based modeling, image compositing, and image processing. Lastly, we demonstrate a few applications of having high dynamic range radiance maps, such as synthesizing realistic motion blur and simulating the response of the human visual system.

提出了一种从传统成像设备拍摄的照片中恢复高动态范围辐射度图的方法。在我们的方法中，场景的多张照片是用不同的曝光量拍摄的。我们的算法使用这些不同曝光的照片恢复成像过程的响应函数，直到比例因子，使用互易性的假设。利用已知的响应函数，该算法可以将多张照片融合成单一的高动态范围辐射度图，其像素值与场景中的真实辐射度值成正比。我们展示了我们使用光化学和数字成像过程获得的图像的方法。我们将讨论这项工作如何适用于涉及数字化照片的计算机图形的许多领域，包括基于图像的建模，图像合成和图像处理。最后，我们展示了一些具有高动态范围辐射图的应用，例如合成逼真的运动模糊和模拟人类视觉系统的响应。

1.Introduction

Digitized photographs are becoming increasingly important in computer graphics. More than ever, scanned images are used as texture maps for geometric models, and recent work in image-based modeling and rendering uses images as the fundamental modeling primitive. Furthermore, many of today’s graphics applications require computer-generated images to mesh seamlessly with real photographic imagery. Properly using photographically acquired imagery in these applications can greatly benefit from an accurate model of the photographic process.

数字照片在计算机图形学中越来越重要。扫描图像比以往任何时候都更常被用作几何模型的纹理映射，而最近基于图像的建模和绘制工作则将图像作为基本的建模原语。此外，当今许多图形应用程序需要计算机生成的图像与真实的摄影图像无缝地结合在一起。在这些应用中正确地使用摄影获得的图像可以从摄影过程的精确模型中大大受益。

When we photograph a scene, either with film or an electronic imaging array, and digitize the photograph to obtain a twodimensional array of “brightness” values, these values are rarely true measurements of relative radiance in the scene. For example, if one pixel has twice the value of another, it is unlikely that it observed twice the radiance. Instead, there is usually an unknown, nonlinear mapping that determines how radiance in the scene becomes pixel values in the image.

当我们用胶片或电子成像阵列拍摄场景，并将照片数字化以获得二维“亮度”值阵列时，这些值很少是场景中相对辐射度的真实测量值。例如，如果一个像素的值是另一个的两倍，那么它不太可能观测到两倍的辐射。相反，通常存在一个未知的非线性映射，它决定了场景中的亮度如何成为图像中的像素值。

This nonlinear mapping is hard to know beforehand because it is actually the composition of several nonlinear mappings that occur in the photographic process. In a conventional camera (see Fig. 1), the film is first exposed to light to form a latent image. The film is then developed to change this latent image into variations in transparency, or density, on the film. The film can then be digitized using a film scanner, which projects light through the film onto an electronic light-sensitive array, converting the image to electrical voltages. These voltages are digitized, and then manipulated before finally being written to the storage medium. If prints of the film are scanned rather than the film itself, then the printing process can also introduce nonlinear mappings.

这种非线性映射很难事先知道，因为它实际上是摄影过程中出现的几个非线性映射的组合。在传统相机(见图1)中，胶片首先暴露在光线下形成潜影。然后冲洗胶卷，使这种潜在的影像变成胶片上透明度或密度的变化。然后可以使用胶片扫描仪将胶片数字化，扫描仪将光线投射到电子光敏阵列上，将图像转换为电压。这些电压被数字化，然后在最终写入存储介质之前进行操作。如果是扫描胶片而不是胶片本身，那么打印过程也会引入非线性映射。

In the first stage of the process, the film response to variations in exposure X (which is , the product of the irradiance E the film receives and the exposure time t) is a non-linear function, called the “characteristic curve” of the film. Noteworthy in the typical characteristic curve is the presence of a small response with no exposure and saturation at high exposures. The development, scanning and digitization processes usually introduce their own nonlinearities which compose to give the aggregate nonlinear relationship between the image pixel exposures X and their values Z.

在这个过程的第一阶段，胶片对曝光X变化的响应(即，胶片接收到的辐照度E与曝光时间的乘积)是一个非线性函数，称为胶片的“特征曲线”。在典型特征曲线中值得注意的是，在高曝光时，无曝光和饱和的响应较小。在图像的发展、扫描和数字化过程中，通常会引入自身的非线性，这些非线性构成了图像像素曝光X与其值Z之间的聚合非线性关系。

Digital cameras, which use charge coupled device (CCD) arrays to image the scene, are prone to the same difficulties. Although the charge collected by a CCD element is proportional to its irradiance, most digital cameras apply a nonlinear mapping to the CCD outputs before they are written to the storage medium. This nonlinear mapping is used in various ways to mimic the response characteristics of film, anticipate nonlinear responses in the display device, and often to convert 12-bit output from the CCD’s analog-to-digital converters to 8-bit values commonly used to store images. As with film, the most significant nonlinearity in the response curve is at its saturation point, where any pixel with a radiance above a certain level is mapped to the same maximum image value.

使用电荷耦合器件阵列(CCD)对场景进行成像的数码相机也容易遇到同样的困难。虽然电荷耦合器件所收集的电荷与其辐照度成正比，但大多数数码相机在将电荷耦合器件输出写入存储介质之前，都会对其进行非线性映射。这种非线性映射用于模拟胶片的响应特性，预测显示设备中的非线性响应，并常常将CCD模数转换器的12位输出转换为通常用于存储图像的8位值。与胶片一样，响应曲线中最显著的非线性是在饱和点处，在饱和点处，任何辐射度高于某一水平的像素都映射到相同的最大图像值。

Why is this any problem at all? The most obvious difficulty, as any amateur or professional photographer knows, is that of limited dynamic range—one has to choose the range of radiance values that are of interest and determine the exposure time suitably. Sunlit scenes, and scenes with shiny materials and artificial light sources, often have extreme differences in radiance values that are impossible to capture without either under-exposing or saturating the film. To cover the full dynamic range in such a scene, one can take a series of photographs with different exposures. This then poses a problem: how can we combine these separate images into a composite radiance map? Here the fact that the mapping from scene radiance to pixel values is unknown and nonlinear begins to haunt us. The purpose of this paper is to present a simple technique for recovering this response function, up to a scale factor, using nothing more than a set of photographs taken with varying, known exposure durations. With this mapping, we then use the pixel values from all available photographs to construct an accurate map of the radiance in the scene, up to a factor of scale. This radiance map will cover the entire dynamic range captured by the original photographs.

这有什么问题吗?任何业余或专业摄影师都知道，最明显的困难是动态范围有限，必须选择感兴趣的辐射度值范围，并适当确定曝光时间。阳光照射的场景，以及使用闪亮材料和人造光源的场景，通常在亮度值上存在极端的差异，如果没有曝光不足或胶片饱和，就不可能捕捉到这种差异。为了在这样一个场景中覆盖整个动态范围，人们可以拍摄一系列不同曝光的照片。这就产生了一个问题：我们如何将这些独立的图像组合成一个复合辐射度图。在这里，从场景辐射到像素值的映射是未知的和非线性的，这一事实开始困扰我们。本文的目的是提出一种简单的技术来恢复这个响应函数，直到一个比例因子，使用的只是一组不同的照片，已知的曝光时间。有了这种映射，我们就可以使用所有可用照片的像素值来构建场景中辐射的精确映射，直到比例系数。这幅辐射图将覆盖原始照片所捕获的整个动态范围。

图1 Image Acquisition Pipeline 显示场景亮度如何成为像素值的胶卷和数码相机。在曝光、显影、扫描、数字化和重映射过程中，可能会出现未知的非线性映射。本文算法确定了一组不同曝光图像从场景辐射度L到像素值Z的聚合映射。

1.1 Application

Our technique of deriving imaging response functions and recovering high dynamic range radiance maps has many possible applications in computer graphics:

我们的成像响应函数的推导和高动态范围辐射度图的恢复技术在计算机图形学中有许多可能的应用：

Image-based modeling and rendering

Image-based modeling and rendering systems to date (e.g. [11, 15, 2, 3, 12, 6, 17]) make the assumption that all the images are taken with the same exposure settings and film response functions. However, almost any large-scale environment will have some areas that are much brighter than others, making it impossible to adequately photograph the scene using a single exposure setting. In indoor scenes with windows, this situation often arises within the field of view of a single photograph, since the areas visible through the windows can be far brighter than the areas inside the building.

基于图像的建模和渲染系统(如[11,15,2,3,12,6,17])假定所有的图像都是在相同的曝光设置和胶片响应函数下拍摄的。然而，几乎任何大型环境都会有一些区域比其他区域更明亮，这使得使用单一曝光设置无法充分拍摄场景。在有窗户的室内场景中，这种情况经常出现在一张照片的视野内，因为透过窗户可以看到的区域比建筑内部的区域要明亮得多。

By determining the response functions of the imaging device, the method presented here allows one to correctly fuse pixel data from photographs taken at different exposure settings. As a result, one can properly photograph outdoor areas with short exposures, and indoor areas with longer exposures, without creating inconsistencies in the data set. Furthermore, knowing the response functions can be helpful in merging photographs taken with different imaging systems, such as video cameras, digital cameras, and film cameras with various film stocks and digitization processes.

通过确定成像设备的响应函数，本文提出的方法可以正确地融合不同曝光设置下拍摄的照片中的像素数据。因此，人们可以适当地拍摄短曝光的室外区域和长曝光的室内区域，而不会造成数据集的不一致。此外，了解响应函数有助于将所拍摄的照片与不同的成像系统(如摄像机、数码相机和胶片相机)结合起来，这些成像系统具有不同的胶片库存和数字化过程。

The area of image-based modeling and rendering is working toward recovering more advanced reflection models (up to complete BRDF’s) of the surfaces in the scene (e.g. [21]). These methods, which involve observing surface radiance in various directions under various lighting conditions, require absolute radiance values rather than the nonlinearly mapped pixel values found in conventional images. Just as important, the recovery of high dynamic range images will allow these methods to obtain accurate radiance values from surface specularities and from incident light sources. Such higher radiance values usually become clamped in conventional images.

基于图像的建模和渲染领域正致力于恢复场景中表面(如[21])更高级的反射模型(直到完成BRDF's)。这些方法包括在不同光照条件下对不同方向的表面辐射度进行观测，需要的是绝对辐射度值，而不是传统图像中的非线性映射像素值。同样重要的是，对高动态范围图像的恢复将使这些方法能够从表面反射和入射光源获得精确的辐射值。这种较高的辐射度值通常在传统图像中被夹住。

Image processing

Most image processing operations, such as blurring, edge detection, color correction, and image correspondence, expect pixel values to be proportional to the scene radiance. Because of nonlinear image response, especially at the point of saturation, these operations can produce incorrect results for conventional images.

大多数图像处理操作，如模糊、边缘检测、颜色校正和图像对应，都希望像素值与场景亮度成比例。由于图像的非线性响应，特别是在饱和点处，这些操作会对传统图像产生不正确的结果。

In computer graphics, one common image processing operation is the application of synthetic motion blur to images. In our results (Section 3), we will show that using true radiance maps produces significantly more realistic motion blur effects for high dynamic range scenes.

在计算机图形学中，一种常见的图像处理操作是将合成运动模糊应用于图像。在我们的结果(第3部分)中，我们将展示使用真实的辐射贴图为高动态范围场景产生更逼真的运动模糊效果。

Image compositing

Many applications in computer graphics involve compositing image data from images obtained by different processes. For example, a background matte might be shot with a still camera, live action might be shot with a different film stock or scanning process, and CG elements would be produced by rendering algorithms. When there are significant differences in the response curves of these imaging processes, the composite image can be visually unconvincing. The technique presented in this paper provides a convenient and robust method of determining the overall response curve of any imaging process, allowing images from different processes to be used consistently as radiance maps. Furthermore, the recovered response curves can be inverted to render the composite radiance map as if it had been photographed with any of the original imaging processes, or a different imaging process entirely.

计算机图形学中的许多应用涉及到从不同处理过程获得的图像中合成图像数据。例如，背景哑光可以用静态相机拍摄，真人动作可以用不同的胶片或扫描过程拍摄，CG元素可以通过渲染算法生成。当这些成像过程的响应曲线存在显著差异时，合成图像在视觉上可能无法令人信服。本文提出的技术提供了一种方便、鲁棒的方法来确定任何成像过程的整体响应曲线，允许不同过程的图像被一致地用作辐射度图。此外，还可以将恢复的响应曲线倒置，以呈现复合辐射度图，就好像它是用任何原始成像过程拍摄的，或者是完全不同的成像过程拍摄的。

A research tool

One goal of computer graphics is to simulate the image formation process in a way that produces results that are consistent with what happens in the real world. Recovering radiance maps of real-world scenes should allow more quantitative evaluations of rendering algorithms to be made in addition to the qualitative scrutiny they traditionally receive. In particular, the method should be useful for developing reflectance and illumination models, and comparing global illumination solutions against ground truth data.

计算机图形学的目标之一是模拟图像的形成过程，以产生与现实世界中发生的事情相一致的结果。恢复真实场景的辐射度图应该允许对渲染算法进行更多的定量评估，而不是传统的定性审查。该方法尤其适用于建立反射率和光照模型，并将全局光照解与地面真值数据进行比较。

Rendering high dynamic range scenes on conventional display devices is the subject of considerable previous work, including [20, 16, 5, 23]. The work presented in this paper will allow such methods to be tested on real radiance maps in addition to synthetically computed radiance solutions.

在传统显示设备上绘制高动态范围场景是前人大量工作的课题，包括[20,16,5,23]。本文所提出的工作将允许这些方法在实际辐射图上测试，除了综合计算辐射度的解决方案。

1.2 Background

The photochemical processes involved in silver halide photography have been the subject of continued innovation and research ever since the invention of the daguerretype in 1839. [18] and [8] provide a comprehensive treatment of the theory and mechanisms involved. For the newer technology of solid-state imaging with charge coupled devices, [19] is an excellent reference. The technical and artistic problem of representing the dynamic range of a natural scene on the limited range of film has concerned photographers from the early days – [1] presents one of the best known systems to choose shutter speeds, lens apertures, and developing conditions to best coerce the dynamic range of a scene to fit into what is possible on a print. In scientific applications of photography, such as in astronomy, the nonlinear film response has been addressed by suitable calibration procedures. It is our objective instead to develop a simple self-calibrating procedure not requiring calibration charts or photometric measuring devices.

自1839年达盖尔照相法发明以来，卤化银照相所涉及的光化学过程一直是不断创新和研究的主题。[18]和[8]对所涉及的理论和机制进行了全面的论述。对于电荷耦合器件固态成像的新技术，[19]是一个很好的参考。在有限范围的胶片中表现自然场景的动态范围的技术和艺术问题涉及早期的摄影师 -  [1]提出了一个最著名的系统选择快门速度，镜头光圈，和发展条件最好强迫一个场景的动态范围，以适应打印什么是可能的。在摄影的科学应用中，例如在天文学中，用适当的校准程序处理了非线性胶片响应。我们的目标是开发一种简单的自校准程序，不需要校准图表或光度测量设备。

In previous work, [13] used multiple flux integration times of a CCD array to acquire extended dynamic range images. Since direct CCD outputs were available, the work did not need to deal with the problem of nonlinear pixel value response. [14] addressed the problem of nonlinear response but provide a rather limited method of recovering the response curve. Specifically, a parametric form of the response curve is arbitrarily assumed, there is no satisfactory treatment of image noise, and the recovery process makes only partial use of the available data.

在之前的工作中，[13]利用CCD阵列的多次通量积分时间来获取扩展的动态范围图像。由于CCD可以直接输出，因此不需要处理像素值的非线性响应问题。[14]解决了非线性响应问题，但提供了一种相当有限的恢复响应曲线的方法。具体来说，响应曲线的参数形式是任意假设的，图像噪声没有得到满意的处理，恢复过程只部分利用了可用数据。

2 The Algorithm

This section presents our algorithm for recovering the film response function, and then presents our method of reconstructing the high dynamic range radiance image from the multiple photographs. We describe the algorithm assuming a grayscale imaging device. We discuss how to deal with color in Section 2.6.

本节给出了恢复胶片响应函数的算法，并给出了从多幅图像中重建高动态范围辐射图像的方法。我们描述了假设灰度成像设备的算法。我们将在2.6节讨论如何处理颜色。

2.1 Film Response Recovery

Our algorithm is based on exploiting a physical property of imaging systems, both photochemical and electronic, known as reciprocity.

我们的算法是基于利用成像系统的物理特性，即光化学和电子的互易性。

Let us consider photographic film first. The response of a film to variations in exposure is summarized by the characteristic curve (or Hurter-Driffield curve). This is a graph of the optical density D of the processed film against the logarithm of the exposure X to which it has been subjected. The exposure X is defined as the product of the irradiance E at the film and exposure time, , so that its units are . Key to the very concept of the characteristic curve is the assumption that only the product E is important, that halving E and doubling will not change the resulting optical density D. Under extreme conditions (very large or very low t ), the reciprocity assumption can break down, a situation described as reciprocity failure. In typical print films, reciprocity holds to within 3 1 stop1 for exposure times of 10 seconds to 1/10,000 of a second.2 In the case of charge coupled arrays, reciprocity holds under the assumption that each site measures the total number of photons it absorbs during the integration time.

让我们先考虑胶卷。胶片对曝光变化的响应可用特征曲线(或Hurter-Driffield曲线)来概括。这是处理过的胶片的光密度D与它所受到的曝光X的对数的关系图。曝光X定义为胶片上的辐照度E与曝光时间的乘积，因此它的单位是。特征曲线概念的关键是假设只有乘积E是重要的，将E减半并将加倍不会改变结果的光密度D。在极端条件下(非常大或非常小的t)，互惠假设可以分解，这种情况称为互惠失效。在典型的印刷胶中，当曝光时间为10秒到1/ 10000秒时，相互作用保持在1/3 stop1内。在电荷耦合阵列的情况下，互易性是在每个位置测量其在积分时间内吸收的光子总数的假设下成立的。

After the development, scanning and digitization processes, we obtain a digital number Z, which is a nonlinear function of the original exposure X at the pixel. Let us call this function f, which is the composition of the characteristic curve of the film as well as all the nonlinearities introduced by the later processing steps. Our first goal will be to recover this function f. Once we have that, we can compute the exposure X at each pixel, as . We make the reasonable assumption that the function f is monotonically increasing, so its inverse is well defined. Knowing the exposure X and the exposure time , the irradiance E is recovered as E = X/, which we will take to be proportional to the radiance L in the scene.

经过发展、扫描和数字化处理，我们得到了一个数字Z，它是原始曝光X在像素处的非线性函数。我们称这个函数为f，它是胶片特征曲线的组成，也是后期处理步骤引入的所有非线性的组成。我们的第一个目标是恢复这个函数f。一旦我们有了它，我们就可以计算每个像素处的曝光X，因为。我们做了一个合理的假设，函数f是单调递增的，所以它的逆是有定义的。已知曝光X和曝光时间，将辐照度E恢复为E = X/，取其与场景中的辐照度L成正比。

Before proceeding further, we should discuss the consequences of the spectral response of the sensor. The exposure X should be thought of as a function of wavelength , and the abscissa on the characteristic curve should be the integral R where  is the spectral response of the sensing element at the pixel location. Strictly speaking, our use of irradiance, a radiometric quantity, is not justified. However, the spectral response of the sensor site may not be the photopic luminosity function , so the photometric term illuminance is not justified either. In what follows, we will use the term irradiance, while urging the reader to remember that the quantities we will be dealing with are weighted by the spectral response at the sensor site. For color photography, the color channels may be treated separately.

在进一步讨论之前，我们应该讨论传感器光谱响应的后果。曝光X应该被认为是波长的函数，特征曲线上的横坐标应该是积分，其中是像素位置处的传感元件的光谱响应。严格地说，我们使用的辐照度，一个辐射量，是不合理的。但是，由于传感器位置的光谱响应可能不是光度函数，因此光度项照度也不合理。在下面，我们将使用术语辐照度，同时敦促读者记住，我们将处理的数量是由传感器现场的光谱响应加权的。对于彩色摄影，彩色通道可以单独处理。

The input to our algorithm is a number of digitized photographs taken from the same vantage point with different known exposure durations . We will assume that the scene is static and that this process is completed quickly enough that lighting changes can be safely ignored. It can then be assumed that the film irradiance values Ei for each pixel i are constant. We will denote pixel values by Zij where i is a spatial index over pixels and j indexes over exposure times . We may now write down the film reciprocity equation as:

我们的算法的输入是一些从相同的有利位置拍摄的不同已知曝光时间的数字化照片。我们将假设场景是静态的，并且这个过程完成得足够快，可以安全地忽略灯光的变化。然后可以假设每个像素i的胶片辐照度值Ei是常数。我们将通过Zij表示像素值，其中i是像素上的空间索引和曝光时间上的j个索引。我们现在可以把胶片的互易方程写成：

(1)

Since we assume f is monotonic, it is invertible, and we can rewrite (1) as:

因为我们假设f是单调的，它是可逆的，我们可以把(1)重写为：

Taking the natural logarithm of both sides, we have:

两边同时取自然对数：

To simplify notation, let us define function g = ln f 1. We then have the set of equations:

为了简化符号，我们定义函数。然后我们得到了方程组：

(2)

where i ranges over pixels and j ranges over exposure durations. In this set of equations, the Zij are known, as are the . The unknowns are the irradiances Ei, as well as the function g, although we assume that g is smooth and monotonic.

i的范围是像素，j的范围是曝光时间。在这个方程组中，Zij和是已知的。未知数是辐照度Ei，还有函数g，尽管我们假设g是光滑单调的。

We wish to recover the function g and the irradiances Ei that best satisfy the set of equations arising from Equation 2 in a least-squared error sense. We note that recovering g only requires recovering the finite number of values that g(z) can take since the domain of Z, pixel brightness values, is finite. Letting Zmin and Zmax be the least and greatest pixel values (integers), N be the number of pixel locations and P be the number of photographs, we formulate the problem as one of finding the (Zmax - Zmin + 1) values of g(Z) and the N values of ln Ei that minimize the following quadratic objective function:

我们希望在误差最小的平方意义上恢复函数g和最能满足由方程2产生的方程组的辐照度Ei。我们注意到，恢复g只需要恢复g(z)可以取的有限数量的值，因为z的域，即像素亮度值，是有限的。假设Zmin和Zmax是最小和最大像素值（整数），N是像素位置的数量，P是照片的数量，我们将问题表示为找到g(Z)的（Zmax - Zmin + 1）值和ln Ei的N值之一，使下面的二次目标函数最小化：

(3)

The first term ensures that the solution satisfies the set of equations arising from Equation 2 in a least squares sense. The second term is a smoothness term on the sum of squared values of the second derivative of g to ensure that the function g is smooth; in this discrete setting we use . This smoothness term is essential to the formulation in that it provides coupling between the values g(z) in the minimization. The scalar  weights the smoothness term relative to the data fitting term, and should be chosen appropriately for the amount of noise expected in the Zij measurements.

第一项保证解在最小二乘意义上满足由方程2导出的方程组。第二项是平滑项对g的二阶导数的平方值求和确保函数g是平滑的；在这个离散的设置中，我们使用，这个平滑项对于公式至关重要，因为它提供了最小值g(z)之间的耦合。该标量对平滑项相对于数据拟合项进行加权，并应根据Zij测量中期望的噪声量进行适当选择。

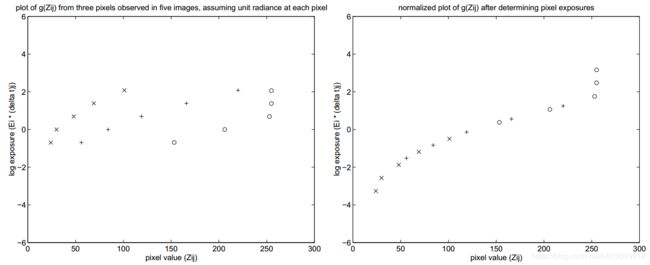
Because it is quadratic in the Ei’s and g(z)’s, minimizing O is a straightforward linear least squares problem. The overdetermined system of linear equations is robustly solved using the singular value decomposition (SVD) method. An intuitive explanation of the procedure may be found in Fig. 2.

因为它是Ei和g(z)的二次函数，所以最小化O是一个简单的线性最小二乘问题。采用奇异值分解(SVD)方法对线性方程组的超定问题进行了稳健求解。图2可以直观地解释这个过程。

We need to make three additional points to complete our description of the algorithm:

我们需要另外提出三点来完成对算法的描述：

First, the solution for the g(z) and Ei values can only be up to a single scale factor . If each log irradiance value ln Ei were replaced by ln Ei + , and the function g replaced by g + , the system of equations 2 and also the objective function O would remain unchanged. To establish a scale factor, we introduce the additional constraint g(Zmid) = 0, where Zmid = 1/2 (Zmin + Zmax), simply by adding this as an equation in the linear system. The meaning of this constraint is that a pixel with value midway between Zmin and Zmax will be assumed to have unit exposure.

首先，g(z)和Ei值的解只能是单个比例因子。如果将每个对数辐照度值替换为，函数g替换为，则方程组2和目标函数O不变。为了建立一个比例因子，我们引入额外的约束条件g(Zmid) = 0，其中Zmid = 1/2(Zmin + Zmax)，只需将其作为线性系统中的方程相加即可。这个约束的含义是，假设一个值位于Zmin和Zmax之间的像素具有单位曝光。

Second, the solution can be made to have a much better fit by anticipating the basic shape of the response function. Since g(z) will typically have a steep slope near Zmin and Zmax, we should expect that g(z) will be less smooth and will fit the data more poorly near these extremes. To recognize this, we can introduce a weighting function w(z) to emphasize the smoothness and fitting terms toward the middle of the curve. A sensible choice of w is a simple hat function:

其次，通过预测响应函数的基本形状，可以使求解具有更好的拟合性。由于g(z)通常在Zmin和Zmax附近有一个陡峭的斜率，所以我们应该预计g(z)将不太平滑，并且在这些极端附近更不适合数据。为了认识到这一点，我们可以引入加权函数w(z)来强调曲线中间的平滑度和拟合项。明智地选择w是一个简单的hat函数：

(4)

Equation 3 now becomes:

方程3变成：

Finally, we need not use every available pixel site in this solution procedure. Given measurements of N pixels in P photographs, we have to solve for N values of ln Ei and (Zmax-Zmin ) samples of g. To ensure a sufficiently overdetermined system, we want N (P-1) > (Zmax-Zmin ). For the pixel value range (Zmax-Zmin ) = 255, P = 11 photographs, a choice of N on the order of 50 pixels is more than adequate. Since the size of the system of linear equations arising from Equation 3 is on the order of NxP + Zmax-Zmin, computational complexity considerations make it impractical to use every pixel location in this algorithm. Clearly, the pixel locations should be chosen so that they have a reasonably even distribution of pixel values from Zmin to Zmax, and so that they are spatially well distributed in the image. Furthermore, the pixels are best sampled from regions of the image with low intensity variance so that radiance can be assumed to be constant across the area of the pixel, and the effect of optical blur of the imaging system is minimized. So far we have performed this task by hand, though it could easily be automated.

最后，我们不需要在这个解决方案过程中使用所有可用的像素站点。给定P张照片中的N个像素的测量值，我们必须解出g的lnEi和(Zmax-Zmin)样本的N个值。为了确保一个充分确定的系统，我们需要N (P-1) > (Zmax-Zmin)。对于像素值范围(Zmax-Zmin) = 255, P = 11张照片，在50像素的顺序上选择N是绰绰有余的。由于由式3导出的线性方程组的大小为NxP + Zmax-Zmin阶，计算复杂度的考虑使得在该算法中使用每个像素的位置是不切实际的。显然，选择像素的位置是为了使像素值在Zmin到Zmax之间具有合理均匀的分布，使像素值在图像中具有良好的空间分布。此外，从低强度方差的图像区域中提取的像素是最优的采样点，这样可以假定辐射度在像素区域内是恒定的，从而最小化成像系统的光学模糊效应。到目前为止，我们已经手工完成了这项任务，尽管它很容易实现自动化。

Note that we have not explicitly enforced the constraint that g must be a monotonic function. If desired, this can be done by transforming the problem to a non-negative least squares problem. We have not found it necessary because, in our experience, the smoothness penalty term is enough to make the estimated g monotonic in addition to being smooth

注意，我们没有明确地规定g一定是一个单调函数。如果需要，可以将问题转换成非负最小二乘问题。我们没有发现它的必要性，因为在我们的经验中，光滑性惩罚项足够使估计的g单调除了光滑。

To show its simplicity, the MATLAB routine we used to minimize Equation 5 is included in the Appendix. Running times are on the order of a few seconds.

为了显示它的简单性，我们用来最小化方程5的MATLAB例程包含在附录中。运行时间大约是几秒钟。

2.2 Constructing the High Dynamic Range Radiance Map

Once the response curve g is recovered, it can be used to quickly convert pixel values to relative radiance values, assuming the exposure is known. Note that the curve can be used to determine radiance values in any image(s) acquired by the imaging process associated with g, not just the images used to recover the response function.

一旦恢复响应曲线g，它可以用来快速转换像素值到相对辐射值，假设曝光已知。注意，曲线可以用来确定与g相关的成像过程获得的任何图像的辐射值，而不仅仅是用来恢复响应函数的图像。

From Equation 2, we obtain:

从方程2中，我们得到：

(5)

For robustness, and to recover high dynamic range radiance values, we should use all the available exposures for a particular pixel to compute its radiance. For this, we reuse the weighting function in Equation 4 to give higher weight to exposures in which the pixel’s value is closer to the middle of the response function:

为了鲁棒性和恢复高动态范围的辐射值，我们应该使用特定像素的所有可用曝光来计算其辐射。为此，我们重新使用方程4中的加权函数，使像素值更接近响应函数中部的曝光具有更高的权重：

(6)

Combining the multiple exposures has the effect of reducing noise in the recovered radiance values. It also reduces the effects
of imaging artifacts such as film grain. Since the weighting function ignores saturated pixel values, “blooming” artifacts5 have little impact on the reconstructed radiance values.

组合多次曝光具有降低恢复的辐射值中的噪声的效果。 它还可以减少成像伪像（如胶片颗粒）的影响。 由于加权函数忽略饱和像素值，因此晕染伪影对重建的辐射值几乎没有影响。

2.2.1 Storage

In our implementation the recovered radiance map is computed as an array of single-precision floating point values. For efficiency, the map can be converted to the image format used in the RADIANCE [22] simulation and rendering system, which uses just eight bits for each of the mantissa and exponent. This format is particularly compact for color radiance maps, since it stores just one exponent value for all three color values at each pixel. Thus, in this format, a high dynamic range radiance map requires just one third more storage than a conventional RGB image.

在我们的实现中，恢复的辐射图被计算为一个单精度浮点值数组。为了提高效率，可以将映射转换为RADIANCE模拟和呈现系统中使用的图像格式，每个尾数和指数仅使用8位。这种格式特别适合于彩色辐射图，因为它在每个像素上只存储三个颜色值的一个指数值。因此，在这种格式中，一个高动态范围辐射亮度映射只需要比传统RGB图像多三分之一的存储空间。

2.3 How many images are necessary?

To decide on the number of images needed for the technique, it is convenient to consider the two aspects of the process:

为了确定技术所需的图像数量，可以方便地考虑过程的两个方面：

1. Recovering the film response curve: This requires a minimum of two photographs. Whether two photographs are enough
can be understood in terms of the heuristic explanation of the process of film response curve recovery shown in Fig. 2.
If the scene has sufficiently many different radiance values, the entire curve can, in principle, be assembled by sliding together the sampled curve segments, each with only two samples. Note that the photos must be similar enough in their exposure amounts that some pixels fall into the working range6 of the film in both images; otherwise, there is no information to relate the exposures to each other. Obviously, using more than two images with differing exposure times improves performance with respect to noise sensitivity.

1.恢复胶片响应曲线:这至少需要两张照片。从图2所示的胶片响应曲线恢复过程的启发解释可以理解两张照片是否足够。如果场景中有足够多的不同的辐射度值，原则上，整条曲线可以通过将采样曲线段滑动到一起来组装，每个采样段只有两个样本。请注意，两张照片的曝光量必须足够相似，以使两张照片中的某些像素落在胶片的工作范围内;否则，就没有信息来联系到彼此的暴光。显然，使用超过两张不同曝光时间的图像可以提高噪声灵敏度的性能。

2. Recovering a radiance map given the film response curve: The number of photographs needed here is a function of the dynamic range of radiance values in the scene. Suppose the range of maximum to minimum radiance values that we are interested in recovering accurately is R, and the film is capable of representing in its working range a dynamic range of F .
Then the minimum number of photographs needed is R/F to ensure that every part of the scene is imaged in at least one
photograph at an exposure duration that puts it in the working range of the film response curve. As in recovering the response curve, using more photographs than strictly necessary will result in better noise sensitivity.

2.根据胶片响应曲线恢复亮度图：这里需要的照片数量是场景中亮度值的动态范围的函数。假设我们感兴趣的准确恢复的最大到最小辐射度值的范围是R，并且胶片能够在其工作范围内表示F的动态范围。然后，需要的最小照片数量是R/F，以确保场景的每个部分都至少在一张照片中成像，曝光时间使其处于胶片响应曲线的工作范围内。正如在恢复响应曲线，使用更多的照片将导致更好的噪声灵敏度。

If one wanted to use as few photographs as possible, one might first recover the response curve of the imaging process by photographing a scene containing a diverse range of radiance values at three or four different exposures, differing by perhaps one or two stops. This response curve could be used to determine the working range of the imaging process, which for the processes we have seen would be as many as five or six stops. For the remainder of the shoot, the photographer could decide for any particular scene the number of shots necessary to cover its entire dynamic range. For diffuse indoor scenes, only one exposure might be necessary; for scenes with high dynamic range, several would be necessary. By recording the exposure amount for each shot, the images could then be converted to radiance maps using the pre-computed response curve.

如果一个人想要尽可能少地使用照片，他可以首先通过拍摄一个场景来恢复成像过程的响应曲线，这个场景包含了三到四次不同曝光下不同范围的辐射值，可能相差一到两stop。这个响应曲线可以用来确定成像过程的工作范围，对于我们已经看到的过程，可能需要5到6个stop。对于拍摄的剩余部分，摄影师可以为任何特定场景决定需要拍摄的镜头数量，以覆盖整个动态范围。对于漫反射的室内场景，可能只需要一次曝光；对于动态范围大的场景，需要几个场景。通过记录每个镜头的曝光量，然后可以使用预先计算的响应曲线将图像转换为辐射度图。

图2 在左边的图中，x符号代表了g曲线的样本，这些样本来自于5种不同的已知暴露条件下的一个像素的数字值，使用公式2。未知的lnEi的辐照度被假设为0。注意g曲线的形状是正确的，尽管它在垂直比例尺上的位置是任意的，对应于未知的lnEi。+和。符号表示考虑其他两个像素得到的g曲线段样本；同样，每一段的垂直位置是任意的。从本质上说，我们在优化过程中要实现的是将3个采样曲线段上下滑动(通过调整它们的ln Ei)，直到它们“对齐”成一条光滑的单调曲线，如图所示。复合曲线的垂直位置仍然是任意的。

2.4 Recovering extended dynamic range from single exposures

Most commericially available film scanners can detect reasonably close to the full range of useful densities present in film. However, many of these scanners (as well as the Kodak PhotoCD process) produce 8-bit-per-channel images designed to be viewed on a screen or printed on paper. Print film, however, records a significantly greater dynamic range than can be displayed with either of these media. As a result, such scanners deliver only a portion of the detected dynamic range of print film in a single scan, discarding information in either high or low density regions. The portion of the detected dynamic range that is delivered can usually be influenced by “brightness” or “density adjustment” controls.

大多数商业上可用的胶片扫描器都能合理地探测到接近胶片中所有有用密度的范围。然而，许多这样的扫描仪(以及柯达影印过程)每通道产生8位的图像，这些图像被设计成可以在屏幕上观看或打印在纸上。然而，打印胶片记录的动态范围要比这两种介质显示的动态范围大得多。因此，这种扫描仪在一次扫描中只传送被检测到的印刷胶片动态范围的一部分，在高或低密度区域丢弃信息。被检测到的动态范围的一部分通常会受到亮度或密度调节控制的影响。

The method presented in this paper enables two methods for recovering the full dynamic range of print film which we will briefly
outline. In the first method, the print negative is scanned with the scanner set to scan slide film. Most scanners will then record the entire detectable dynamic range of the film in the resulting image. As before, a series of differently exposed images of the same scene can be used to recover the response function of the imaging system with each of these scanner settings. This response function can then be used to convert individual exposures to radiance maps. Unfortunately, since the resulting image is still 8-bits-per-channel, this results in increased quantization.

本文提出的方法可以实现两种方法来恢复我们将简要概述的打印胶片的全动态范围。在第一种方法中，用扫描仪对打印底片进行扫描以扫描幻灯片。大多数扫描仪将记录整个可检测的动态范围的胶片在结果图像。与以前一样，通过这些扫描仪设置，可以利用同一场景的一系列不同曝光图像恢复成像系统的响应功能。然后，这个响应函数可以用来将单个曝光转换成辐射度图。不幸的是，由于得到的图像仍然是每个通道8位的，这导致了量化的增加。

In the second method, the film can be scanned twice with the scanner set to different density adjustment settings. A series of differently exposed images of the same scene can then be used to recover the response function of the imaging system at each of these density adjustment settings. These two response functions can then be used to combine two scans of any single negative using a similar technique as in Section 2.2.

在第二种方法中，胶片可以被扫描两次，扫描仪设置为不同的密度调整设置。然后，在这些密度调整设置中，同一场景的一系列不同曝光图像可以用来恢复成像系统的响应功能。然后，这两个响应函数可以使用与2.2节类似的技术组合任何单个负值的两个扫描。

2.5 Obtaining Absolute Radiance

For many applications, such as image processing and image compositing, the relative radiance values computed by our method are all that are necessary. If needed, an approximation to the scaling term necessary to convert to absolute radiance can be derived using the ASA of the film and the shutter speeds and exposure amounts in the photographs. With these numbers, formulas that give an approximate prediction of film response can be found in [9]. Such an approximation can be adequate for simulating visual artifacts such as glare, and predicting areas of scotopic retinal response. If desired, one could recover the scaling factor precisely by photographing a calibration luminaire of known radiance, and scaling the radiance
values to agree with the known radiance of the luminaire.
对于许多应用，如图像处理和图像合成，我们的方法计算的相对辐射值是必要的。如果需要，可以利用胶片的ASA、快门速度和照片的曝光量，得出转换成绝对辐射度所需的比例项的近似值。利用这些数字，可以在[9]中找到近似预测胶片响应的公式。这样的近似对于模拟诸如眩光等视觉伪影和预测视网膜暗视反应区域是足够的。如果需要，可以通过拍摄已知亮度的校准灯具来精确地恢复比例因子，并根据已知亮度对亮度值进行缩放。

2.6 Color

Color images, consisting of red, green, and blue channels, can be processed by reconstructing the imaging system response curve for each channel independently. Unfortunately, there will be three unknown scaling factors relating relative radiance to absolute radiance, one for each channel. As a result, different choices of these scaling factors will change the color balance of the radiance map.

彩色图像由红、绿、蓝三个通道组成，分别重建各通道的成像系统响应曲线进行处理。不幸的是，将会有三个未知的比例因子与相对辐射和绝对辐射相关，每个通道一个。因此，这些比例因子的不同选择会改变辐射度图的色彩平衡。

By default, the algorithm chooses the scaling factor such that a pixel with value Zmid will have unit exposure. Thus, any pixel with the RGB value (Zmid; Zmid; Zmid ) will have equal radiance values for R, G, and B, meaning that the pixel is achromatic. If the three channels of the imaging system actually do respond equally to achromatic light in the neighborhood of Zmid, then our procedure correctly reconstructs the relative radiances.

默认情况下，算法选择缩放因子，使值为Zmid的像素具有单位曝光。因此，任何具有RGB值的像素(Zmid;Zmid;Zmid)对R、G、B的辐射度值相等，这意味着像素是消色差的。如果成像系统的三个通道确实对Zmid附近的消色光有相同的响应，那么我们的程序正确地重建了相对辐射。

However, films are usually calibrated to respond achromatically to a particular color of light C, such as sunlight or fluorescent light. In this case, the radiance values of the three channels should be scaled so that the pixel value (Zmid; Zmid; Zmid ) maps to a radiance with the same color ratios as C. To properly model the color response of the entire imaging process rather than just the film response, the scaling terms can be adjusted by photographing a calibration luminaire of known color.

然而，胶片通常被校准以对特定颜色的光如日光或荧光灯做出无色反应。在这种情况下，需要对三个通道的辐射度值进行缩放，使像素值(Zmid;Zmid;Zmid)映射到与C颜色比相同的亮度。为了正确地模拟整个成像过程的颜色响应，而不仅仅是胶片响应，可以通过拍摄已知颜色的标定灯具来调整尺度项。

2.7 Taking virtual photographs

The recovered response functions can also be used to map radiance values back to pixel values for a given exposure t using Equation 1. This process can be thought of as taking a virtual photograph of the radiance map, in that the resulting image will exhibit the response qualities of the modeled imaging system. Note that the response functions used need not be the same response functions used to construct the original radiance map, which allows photographs acquired with one imaging process to be rendered as if they were acquired with another.

恢复后的响应函数还可以使用公式1将给定曝光t的辐射值映射回像素值。这一过程可以被认为是对辐射图的一张虚拟照片，因为生成的图像将显示建模成像系统的响应特性。请注意，使用的响应函数不一定是构造原始辐射图所用的响应函数，这允许用一个成像过程获得的照片被渲染成用另一个成像过程获得的照片。

3 Results

Figures 3-5 show the results of using our algorithm to determine the response curve of a DCS460 digital camera. Eleven grayscale photographs filtered down to 765509 resolution (Fig. 3) were taken at f/8 with exposure times ranging from 30 1 of a second to 30 seconds, with each image receiving twice the exposure of the previous one. The film curve recovered by our algorithm from 45 pixel locations observed across the image sequence is shown in Fig. 4. Note that although CCD image arrays naturally produce linear output, from the curve it is evident that the camera nonlinearly remaps the data, presumably to mimic the response curves found in film. The underlying registered data are shown as light circles underneath
the curve; some outliers are due to sensor artifacts (light horizontal bands across some of the darker images.)

图3-5显示了使用我们的算法确定DCS460数码相机的响应曲线的结果。在f/8拍摄的11张灰度照片被过滤到765x509分辨率(图3)，曝光时间从1/30秒到30秒不等，每张照片的曝光量是前一张照片的两倍。我们的算法从图像序列中观察到的45个像素位置恢复出的胶片曲线如图4所示。请注意，尽管CCD图像阵列自然产生线性输出，但从曲线上可以明显看出，摄像机非线性地重新映射数据，可能是为了模拟胶片中的响应曲线。基础注册数据以曲线下方的光圈表示；一些离群值是由传感器伪影造成的(一些较暗图像上的水平光带)。

Fig. 5 shows the reconstructed high dynamic range radiance map. To display this map, we have taken the logarithm of the radiance values and mapped the range of these values into the range of the display. In this representation, the pixels at the light regions do not saturate, and detail in the shadow regions can be made out, indicating that all of the information from the original image sequence is present in the radiance map. The large range of values present in the radiance map (over four orders of magnitude of useful dynamic range) is shown by the values at the marked pixel locations.

图5为重构的高动态范围辐射度图。为了显示这张地图，我们取了辐射值的对数，并将这些值的范围映射到显示的范围中。在这个表示中，光区域的像素不饱和，阴影区域的细节可以被辨认出来，表明所有来自原始图像序列的信息都存在于辐射图中。辐射度图中出现的大范围的值(超过有用的动态范围的四个数量级)由标记像素位置的值显示。

Figure 6 shows sixteen photographs taken inside a church with a Canon 35mm SLR camera on Fuji 100 ASA color print film. A fisheye 15mm lens set at f/8 was used, with exposure times ranging from 30 seconds to 1/1000 of a second in 1-stop increments. The film was developed professionally and scanned in using a Kodak PhotoCD film scanner. The scanner was set so that it would not individually adjust the brightness and contrast of the images10 to guarantee that each image would be digitized using the same response function.

图6是在富士100彩色胶片上用佳能35mm单反相机在教堂内拍摄的16张照片。使用f/8的鱼眼15mm镜头，曝光时间从30秒到1/1000秒不等，每隔一站增加一次。该胶卷是专业开发的，并在使用柯达胶卷扫描仪扫描。扫描仪的设置使其不会单独调整图像的亮度和对比度，以确保每幅图像都将使用相同的响应函数进行数字化。

An unfortunate aspect of the PhotoCD process is that it does not scan precisely the same area of each negative relative to the extents of the image.11 To counteract this effect, we geometrically registered the images to each other using a using normalized correlation (see [4]) to determine, with sub-pixel accuracy, corresponding pixels between pairs of images

遗憾的是，PhotoCD处理的一个方面是，相对于图像的宽度，它不能精确扫描每个底片的相同区域。为了抵消这种影响，我们使用归一化相关(见[4])对图像进行几何注册，以亚像素精度确定对图像之间的对应像素。

Fig. 7(a-c) shows the response functions for the red, green, and blue channels of the church sequence recovered from 28 pixel locations. Fig. 7(d) shows the recovered red, green, and blue response curves plotted on the same set of axes. From this plot, we can see that while the red and green curves are very consistent, the blue curve rises significantly above the others for low exposure values. This indicates that dark regions in the images exhibit a slight blue cast. Since this artifact is modeled by the response curves, it will not affect the relative radiance values.

图7(a-c)为教堂序列从28个像素位置恢复的红、绿、蓝通道的响应函数。图7(d)为同一组坐标轴上恢复的红、绿、蓝响应曲线。从图中我们可以看出，虽然红色和绿色曲线非常一致，但是蓝色曲线在低曝光值下明显高于其他曲线。这表明图像中的暗区域呈现出轻微的蓝色偏差。 由于此artifact由响应曲线建模，因此不会影响相对辐亮度值。

Fig. 8 interprets the recovered high dynamic range radiance map in a variety of ways. Fig. 8(a) is one of the actual photographs, which lacks detail in its darker regions at the same time that many values within the two rightmost stained glass windows are saturated. Figs. 8(b,c) show the radiance map, linearly scaled to the display device using two different scaling factors. Although one scaling factor is one thousand times the other, there is useful detail in both images. Fig. 8(d) is a false-color image showing radiance values for a grayscale version of the radiance map; the highest listed radiance value is nearly 250,000 times that of the lowest. Figs. 8(e,f) show two renderings of the radiance map using a new tone reproduction algorithm [23]. Although the rightmost stained glass window has radiance values over a thousand times higher than the darker areas
in the rafters, these renderings exhibit detail in both areas.

图8以多种方式解释了恢复后的高动态范围辐射图。图8(a)是实际的照片之一，它在较暗的区域缺乏细节，同时两个最右边的彩色玻璃窗内的许多值都饱和了。图8(b,c)显示了使用两个不同比例因子线性缩放到显示设备的辐射图。虽然一个比例因子是另一个的一千倍，但在这两幅图像中都有有用的细节。图8(d)为辐射度图灰度版本的辐射度值的伪彩色图像；最高的辐射值是最低辐射值的25万倍。图8(e,f)为采用新的色调再现算法[23]的辐射度图的两幅效果图。虽然最右边的彩色玻璃窗的亮度值比椽子上较暗的区域高1000倍以上，但这些渲染图在这两个区域都表现出了细节。

Figure 9 demonstrates two applications of the techniques presented in this paper: accurate signal processing and virtual photography. The task is to simulate the effects of motion blur caused by moving the camera during the exposure. Fig. 9(a) shows the results of convolving an actual, low-dynamic range photograph with a 37 x 1 pixel box filter to simulate horizontal motion blur. Fig. 9(b) shows the results of applying this same filter to the high dynamic range radiance map, and then sending this filtered radiance map back through the recovered film response functions using the same exposure time as in the actual photograph. Because we are seeing this image through the actual image response curves, the two left images are tonally consistent with each other. However, there is a large difference between these two images near the bright spots. In the photograph, the bright radiance values have been clamped to the maximum pixel values by the response function. As a result, these clamped values blur with lower neighboring values and fail to saturate the image in the final result, giving a muddy appearance.

图9展示了本文提出的技术的两个应用：精确信号处理和虚拟摄影。这个任务是模拟在曝光过程中移动相机所造成的运动模糊的效果。图9(a)显示了将实际的低动态范围照片与37x1像素盒滤波器进行卷积以模拟水平运动模糊的结果。图9(b)为将该滤波器应用于高动态范围辐射度图的结果，然后使用与实际照片相同的曝光时间，将该滤波后的辐射度图通过回收的胶片响应函数发送回去。因为我们是通过实际的图像响应曲线看到这个图像的，所以左边的两个图像在音调上是一致的。然而，这两幅图像在亮点附近有很大的差异。在照片中，响应函数将亮度值夹紧到最大像素值。结果，这些夹紧的值与相邻的较低的值模糊，最终无法使图像饱和，呈现浑浊的外观。

In Fig. 9(b), the extremely high pixel values were represented properly in the radiance map and thus remained at values above the level of the response function’s saturation point within most of the blurred region. As a result, the resulting virtual photograph exhibits several crisply-defined saturated regions

在图9(b)中，极高的像素值在辐射度图中得到了恰当的表示，因此在大部分模糊区域内仍保持在响应函数饱和点以上的值。因此，生成的虚拟照片显示了几个由褶皱定义的饱和区域。

Fig. 9(c) is an actual photograph with real motion blur induced by spinning the camera on the tripod during the exposure, which is equal in duration to Fig. 9(a) and the exposure simulated in Fig. 9(b). Clearly, in the bright regions, the blurring effect is qualitatively similar to the synthetic blur in 9(b) but not 9(a). The precise shape of the real motion blur is curved and was not modeled for this demonstration.

图9(c)是在曝光过程中，三脚架上旋转相机所产生的真实运动模糊的实景照片，与图9(a)和图9(b)所模拟的曝光时间相等。显然，在明亮区域，模糊效果在质量上类似于9(b)中的合成模糊，但不是9(a)中的合成模糊。真实运动模糊的精确形状是弯曲的，并没有为这个演示建模。

4 Conclusion

We have presented a simple, practical, robust and accurate method of recovering high dynamic range radiance maps from ordinary photographs. Our method uses the constraint of sensor reciprocity to derive the response function and relative radiance values directly from a set of images taken with different exposures. This work has a wide variety of applications in the areas of image-based modeling and rendering, image processing, and image compositing, a few of which we have demonstrated. It is our hope that this work will be able to help both researchers and practitioners of computer graphics
make much more effective use of digitized photographs.

提出了一种简单、实用、鲁棒、准确的从普通照片中恢复高动态距离辐射幅值的方法。我们的方法利用传感器互易性的约束，直接从一组不同曝光的图像中得到响应函数和相对辐射值。该工作在基于图像的建模和渲染、图像处理和图像合成等领域有着广泛的应用，我们已经演示了其中的一些。我们希望这项工作能够帮助计算机图形学的研究者和实践者更有效地利用数字化照片。

Acknowledgments

The authors wish to thank Tim Hawkins, Carlo S´ equin, David Forsyth, Steve Chenney, Chris Healey, and our reviewers for their valuable help in revising this paper. This research was supported by a Multidisciplinary University Research Initiative on three dimensional direct visualization from ONR and BMDO, grant FDN00014- 96-1-1200.

作者感谢Tim Hawkins、Carlo S equin、David Forsyth、Steve Chenney、Chris Healey以及我们的审稿人对本文的修改提供了宝贵的帮助。本研究得到了来自ONR和BMDO的三维直接可视化的多学科大学研究计划的支持，授予FDN00014- 96-1-1200。