NLP实习笔试面试题汇总四
一、决策树有哪些常用的启发函数?如何对决策树进行剪枝?
- 决策树的分类
离散性决策树:离散性决策树,其目标变量是离散的,如性别:男或女等;
连续性决策树:连续性决策树,其目标变量是连续的,如工资、价格、年龄等;
决策树相关的重要概念:
(1)根结点(Root Node):它表示整个样本集合,并且该节点可以进一步划分成两个或多个子集。
(2)拆分(Splitting):表示将一个结点拆分成多个子集的过程。
(3)决策结点(Decision Node):当一个子结点进一步被拆分成多个子节点时,这个子节点就叫做决策结点。
(4)叶子结点(Leaf/Terminal Node):无法再拆分的结点被称为叶子结点。
(5)剪枝(Pruning):移除决策树中子结点的过程就叫做剪枝,跟拆分过程相反。
(6)分支/子树(Branch/Sub-Tree):一棵决策树的一部分就叫做分支或子树。
(7)父结点和子结点(Paren and Child Node):一个结点被拆分成多个子节点,这个结点就叫做父节点;其拆分后的子结点也叫做子结点。
决策树的构造过程
决策树的构造过程一般分为3个部分,分别是特征选择、决策树生产和决策树裁剪。
(1)特征选择:
特征选择表示从众多的特征中选择一个特征作为当前节点分裂的标准,如何选择特征有不同的量化评估方法,从而衍生出不同的决策树,如ID3(通过信息增益选择特征)、C4.5(通过信息增益比选择特征)、CART(通过Gini指数选择特征)等。
目的(准则):使用某特征对数据集划分之后,各数据子集的纯度要比划分钱的数据集D的纯度高(也就是不确定性要比划分前数据集D的不确定性低)
(2)决策树的生成
根据选择的特征评估标准,从上至下递归地生成子节点,直到数据集不可分则停止决策树停止生长。这个过程实际上就是使用满足划分准则的特征不断的将数据集划分成纯度更高,不确定行更小的子集的过程。对于当前数据集的每一次划分,都希望根据某个特征划分之后的各个子集的纯度更高,不确定性更小。
(3)决策树的裁剪
决策树容易过拟合,一般需要剪枝来缩小树结构规模、缓解过拟合。
决策树的优缺点
- 决策树的优点:
(1)具有可读性,如果给定一个模型,那么过呢据所产生的决策树很容易推理出相应的逻辑表达。
(2)分类速度快,能在相对短的时间内能够对大型数据源做出可行且效果良好的结果。
- 决策树的缺点:
对未知的测试数据未必有好的分类、泛化能力,即可能发生过拟合现象,此时可采用剪枝或随机森林。
常见的决策树算法:
- ID3----最大信息增益
(1)熵
在信息论中,熵(entropy)是随机变量不确定性的度量,也就是熵越大,则随机变量的不确定性越大。设X是一个取有限个值得离散随机变量,其概率分布为:

则随机变量X的熵定义为:
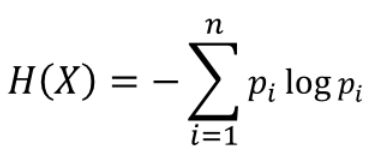
(2)条件熵
设有随机变量(X, Y),其联合概率分布为:

条件熵H(Y|X)表示在已知随机变量X的条件下,随机变量Y的不确定性。随机变量X给定的条件下随机变量Y的条件熵H(Y|X),定义为X给定条件下Y的条件概率分布的熵对X的数学期望:

当熵和条件熵中的概率由数据估计得到时(如极大似然估计),所对应的熵与条件熵分别称为经验熵和经验条件熵。
(3)信息增益
定义:信息增益表示由于得知特征A的信息后儿时的数据集D的分类不确定性减少的程度,定义为:
Gain(D,A) = H(D) – H(D|A)
即集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(H|A)之差。
理解:选择划分后信息增益大的作为划分特征,说明使用该特征后划分得到的子集纯度越高,即不确定性越小。因此我们总是选择当前使得信息增益最大的特征来划分数据集。
缺点:信息增益偏向取值较多的特征(原因:当特征的取值较多时,根据此特征划分更容易得到纯度更高的子集,因此划分后的熵更低,即不确定性更低,因此信息增益更大)

- C4.5----最大信息增益比
C4.5算法与ID3算法很相似,C4.5算法是对ID3算法做了改进,在生成决策树过程中采用信息增益比来选择特征


最大信息增益方法对于可选值较多的方法偏好较大,因其纯度较大。信息增益比对较多值进行惩罚。提供泛化能力。
- ID3只能处理离散变量。C4.5和CART都能处理连续。CART处理连续是将其转为离散。
- ID3和C4.5只能分类任务。CART可以回归。
- ID3对缺失值敏感,C4.5和CART可以处理缺失值。
- 如何对决策树进行剪枝?
决策树容易过拟合,需要剪枝。分为预剪枝和后剪枝
- 预剪枝
预剪枝核心思想在于对树中节点扩展之前,先计算当前划分能否带来模型泛化能力的提升。若不能,则不再继续生长子树。 - 后剪枝
后剪枝核心思想先让算法生成一个完全生长的决策树,然后自底向上计算是否剪枝。剪枝过程将子树切除,用叶节点代替。也可以在验证集上,判断能否提升验证集准确率来决定是否剪枝。
二、GBDT的介绍
梯度提升决策树(Gradient Boosting Decision Tree,GBDT)是Boosting算法中非常流行的一个。GBDT非常好地体现了“从错误中学习”的理念,基于决策树预测的残差进行迭代的学习。
集成学习的两大框架:Bagging和Boosting。Bagging并行化,每个弱分类器可以独立地进行训练,而Boosting弱分类器需要一次生成。在每一轮迭代中,基于已生成的弱分类器集合(即当前模型)的预测结果,新的分类器重点关注那些没有被预测正确的样本。
Gradient Boosting是Boosting中的一大类算法,其基本思想是根据当前模型损失函数的负梯度信息来训练新加入的弱分类器,然后把训练好的分类器以累加的形式加入到现有模型中去。
Gradient Boosting的流程:在每一轮迭代中,首先计算出当前模型在所有样本上的负梯度,然后以该值为目标训练出一个新的弱分类器进行拟合并计算出该弱分类器的权重。最终实现对模型的更新。
采用决策树作为弱分类器的Gradient Boosting算法称为GBDT。GBDT中使用的决策树通常为CART。
由于GBDT是利用残差训练的。预测过程需要把所有树的预测值加起来,得到最后的预测结果。
三、Xgboost与GBDT的区别与联系
XGBoost是一个开源机器学习项目,高效实现了GBDT算法并进行了许多改进。
- GBDT是机器学习算法,XGBoost是该算法的工程实现
- 在使用CART作为基分类器的时候,XGBoost显式地加入了正则项来控制模型复杂度,有利于防止过拟合
- GBDT在模型训练时只使用了代价函数的一阶导数信息,XGBoost对代价函数进行二阶泰勒展开,可以同时使用一阶和二阶函数
- 传统的GBDT采样CART作为基分类器,而XGBoost支持多种类型的基分类器,比如线性分类器
- 传统的GBDT在每轮迭代时使用全部数据,XGBoost支持对数据进行采样
- 传统的GBDT没有设计对缺失值的处理,XGBoost能自动学出缺失值处理策略
四、深度学习优化算法
1. SGD 随机梯度下降
普通的梯度下降法每进行一次 迭代 都需要将所有的样本进行计算,当样本量十分大的时候,会非常消耗计算资源,收敛速度会很慢。尤其如果像ImageNet那样规模的数据,几乎是不可能完成的。同时由于每次计算都考虑了所有的训练数据,也容易造成过拟合。在某种程度上考虑的太多也会丧失随机性 。于是有人提出,既然如此,那可不可以每一次迭代只计算一个样本的loss呢?然后再逐渐遍历所有的样本,完成一轮(epoch)的计算。答案是可以的,虽然每次依据单个样本会产生较大的波动,但是从整体上来看,最终还是可以成功收敛。由于计算量大大减少,计算速度也可以极大地提升。这种逐个样本进行loss计算进行迭代的方法,称之为 Stochasitc Gradient Descent 简称SGD。

2. mini-batch SGD 小批量随机梯度下降
SGD随机梯度下降法对经典的梯度下降法有了极大速度的提升。但有一个问题就是由于过于自由 导致训练的loss波动很大。那么如何可以兼顾经典GD的稳定下降同时又保有SGD的随机特性呢?于是小批量梯度下降法, mini-batch gradient descent 便被提了出来。其主要思想就是每次只拿总训练集的一小部分来训练,比如一共有5000个样本,每次拿100个样本来计算loss,更新参数。50次后完成整个样本集的训练,为一轮(epoch)。由于每次更新用了多个样本来计算loss,就使得loss的计算和参数的更新更加具有代表性。不像原始SGD很容易被某一个样本给带偏 。loss的下降更加稳定,同时小批量的计算,也减少了计算资源的占用。

3. momentum 动量法


4. Adagrad

5. RMSprop

6. Adam

7. Adamax

8. Nadam

说明

此处有各个优化算法的动态视图:https://blog.csdn.net/u012759136/article/details/52302426
五、Dropout
- Dropout简介
1.1 Dropout出现的原因
在机器学习的模型中,如果模型的参数太多,而训练样本又太少,训练出来的模型很容易产生过拟合的现象。在训练神经网络的时候经常会遇到过拟合的问题,过拟合具体表现在:模型在训练数据上损失函数较小,预测准确率较高;但是在测试数据上损失函数比较大,预测准确率较低。
过拟合是很多机器学习的通病。如果模型过拟合,那么得到的模型几乎不能用。为了解决过拟合问题,一般会采用模型集成的方法,即训练多个模型进行组合。此时,训练模型费时就成为一个很大的问题,不仅训练多个模型费时,测试多个模型也是很费时。
综上所述,训练深度神经网络的时候,总是会遇到两大缺点:
(1)容易过拟合
(2)费时
Dropout可以比较有效的缓解过拟合的发生,在一定程度上达到正则化的效果。
1.2 什么是Dropout
在前向传播的时候,让某个神经元的激活值以一定的概率p停止工作,这样可以使模型泛化性更强,因为它不会太依赖某些局部的特征


1.3 为什么说Dropout可以解决过拟合?
(1)取平均的作用: 先回到标准的模型即没有dropout,我们用相同的训练数据去训练5个不同的神经网络,一般会得到5个不同的结果,此时我们可以采用 “5个结果取均值”或者“多数取胜的投票策略”去决定最终结果。例如3个网络判断结果为数字9,那么很有可能真正的结果就是数字9,其它两个网络给出了错误结果。这种“综合起来取平均”的策略通常可以有效防止过拟合问题。因为不同的网络可能产生不同的过拟合,取平均则有可能让一些“相反的”拟合互相抵消。dropout掉不同的隐藏神经元就类似在训练不同的网络,随机删掉一半隐藏神经元导致网络结构已经不同,整个dropout过程就相当于对很多个不同的神经网络取平均。而不同的网络产生不同的过拟合,一些互为“反向”的拟合相互抵消就可以达到整体上减少过拟合。
(2)减少神经元之间复杂的共适应关系: 因为dropout程序导致两个神经元不一定每次都在一个dropout网络中出现。这样权值的更新不再依赖于有固定关系的隐含节点的共同作用,阻止了某些特征仅仅在其它特定特征下才有效果的情况 。迫使网络去学习更加鲁棒的特征 ,这些特征在其它的神经元的随机子集中也存在。换句话说假如我们的神经网络是在做出某种预测,它不应该对一些特定的线索片段太过敏感,即使丢失特定的线索,它也应该可以从众多其它线索中学习一些共同的特征。从这个角度看dropout就有点像L1,L2正则,减少权重使得网络对丢失特定神经元连接的鲁棒性提高。
(3)Dropout类似于性别在生物进化中的角色:物种为了生存往往会倾向于适应这种环境,环境突变则会导致物种难以做出及时反应,性别的出现可以繁衍出适应新环境的变种,有效的阻止过拟合,即避免环境改变时物种可能面临的灭绝。
referance:
https://blog.csdn.net/program_developer/article/details/80737724
