MATLAB一维数据分布情况（稳定程度））

by HPC_ZY

---

搞研究的小伙伴们，经常需要对实验结果进行分析，获取实验的稳定性等。这里提供一个小函数，能对一维数据（实验结果）进行分析，并以图示方式显示其分布情况和稳定性。

---

一、具体实现

主要通过均值方差统计分布实现，不多解释直接上代码。

%   计算一维数据分布情况
%
%   输入：
%       data - 一维数据
%       barnum - （统计）分段数
%       style - 坐标显示风格，0-数据值，1-五线值
%   输出：
%       meandata - 平均值
%       vardata - 标准差
%
%   例：
%       % 随机生成一组数据
%       data = 32+(randn(50,1)-0.5)*5;
%       % 按32段计算并显示分布情况
%       [meandata,vardata] = datadistr(data,32,1);
%
%   注：对于基于统计的分布情况中的各显示参数，不要过于纠结，
%   若真的很感兴趣，可以自己推导。
%
%   by HPC_ZY 20200623

function [meandata,vardata] = datadistr(data,barnum,style)

% 数量、均值、标准差
data = data(:);
num = length(data);
meandata = mean(data);
vardata = sum(sqrt((data-meandata).^2))/num;

%% 直接在数据点上显示分布情况

x = 1:num;
y = data;

% 显示
figure
subplot(211)
plot(x,y,'r*'),hold on
line([0,num+1],[1,1]*meandata,'LineStyle','-','Color',[1,1,1]*0)
line([0,num+1],[1,1]*(meandata+vardata),'LineStyle','-.','Color',[1,1,1]*0.25)
line([0,num+1],[1,1]*(meandata-vardata),'LineStyle','-.','Color',[1,1,1]*0.25)
line([0,num+1],[1,1]*(meandata+3*vardata),'LineStyle','--','Color',[1,1,1]*0.5)
line([0,num+1],[1,1]*(meandata-3*vardata),'LineStyle','--','Color',[1,1,1]*0.5)
axis([0,num+1,meandata-4*vardata,meandata+4*vardata])
legend('data','\mu','+\sigma','-\sigma','+3\sigma','-3\sigma')

if style
    ytick = round((meandata+vardata*[-3,-1,0,1,3])*100)/100;
    yticks(ytick)
    yticklabels(num2cell(ytick))
end

%% 基于统计的分布情况

% 分段统计数量
mindata = min(data)-0.1;
maxdata = max(data)+0.1;
barwidth = (maxdata-mindata)/barnum;
datalist = ceil((data-mindata)/barwidth);
barList = zeros(barnum,1);
for k = 1:num
    barList(datalist(k)) = barList(datalist(k))+1;
end


% 显示（不要纠结各显示参数）
subplot(212)
bar(barList),hold on

if style
    xtick = round(((meandata+[-3,-1,0,1,3]*vardata-mindata)/barwidth+0.5)*100)/100;
    xticks(xtick)
    xticklabels(num2cell(xtick))
else
    xticks(1:barnum)
    xticklabels(num2cell(round((mindata+barwidth*(0.5:barnum))*10)/10))
end

yticks(1:max(barList))
yticklabels(num2cell(1:max(barList)))

line([1,1]*((meandata-mindata)/barwidth+0.5),[0,max(barList)+1],...
    'LineStyle','-','Color',[1,1,1]*0)
line([1,1]*((meandata+vardata-mindata)/barwidth+0.5),[0,max(barList)+1],...
    'LineStyle','-.','Color',[1,1,1]*0.25)
line([1,1]*((meandata-vardata-mindata)/barwidth+0.5),[0,max(barList)+1],...
    'LineStyle','-.','Color',[1,1,1]*0.25)
line([1,1]*((meandata+3*vardata-mindata)/barwidth+0.5),[0,max(barList)+1],...
    'LineStyle','--','Color',[1,1,1]*0.5)
line([1,1]*((meandata-3*vardata-mindata)/barwidth+0.5),[0,max(barList)+1],...
    'LineStyle','--','Color',[1,1,1]*0.5)

gaussx = ((meandata-3*vardata-mindata)/barwidth-0.5):0.1:((meandata+3*vardata-mindata)/barwidth+1);
gaussy = max(barList+0.5)*exp(-(gaussx-((meandata-mindata)/barwidth+0.5)).^2/2/(vardata/barwidth)^2);
plot(gaussx,gaussy,'r--')
legend('data','\mu','+\sigma','-\sigma','+3\sigma','-3\sigma','NDC')
axis([(meandata-4*vardata-mindata)/barwidth-0.5,...
    (meandata+4*vardata-mindata)/barwidth+0.5,0,max(barList+1)])

end

二、测试

通过以下两个实例，大概演示不同参数的效果

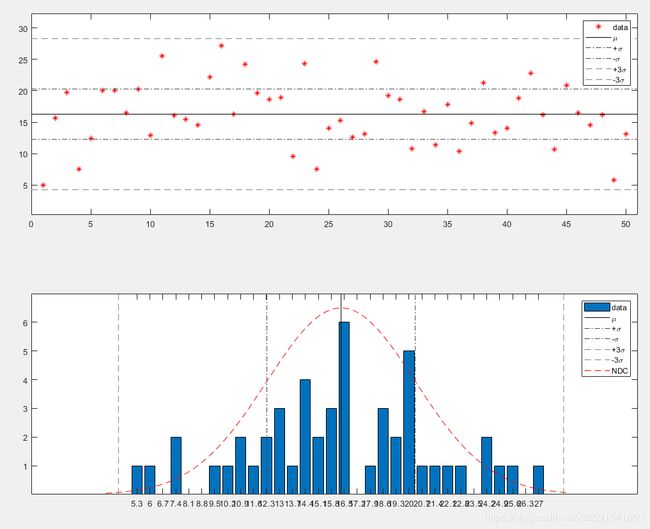
1. 32段+坐标值

% 随机生成一组数据
data = 20+(randn(50,1)-0.5)*5;
% 按32段计算并显示分布情况
[meandata,vardata] = datadistr(data,32,0);

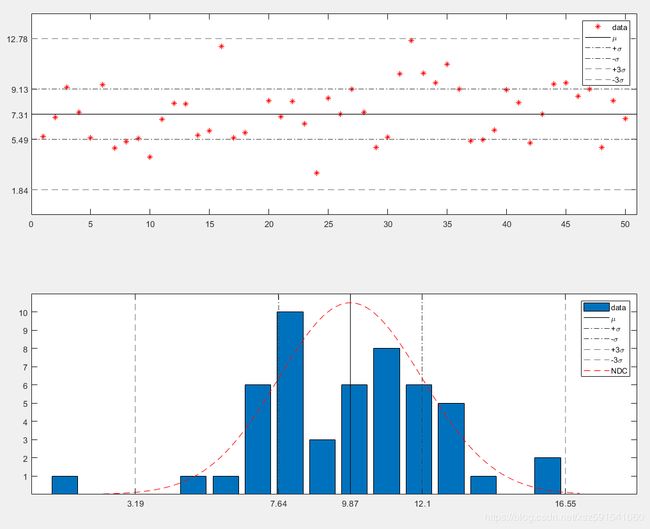
2. 16段+五线值

% 随机生成一组数据
data = 8+(randn(50,1)-0.5)*2;
% 按16段计算并显示分布情况
[meandata,vardata] = datadistr(data,16,1);

三、其他

欢迎复制拿走，如果觉得还行不妨留言点赞，爱了爱了