网络与信息安全领域专项赛 writeup
crypto sm4:
题目提示这是一个sm4加密的题目,给出了key和密文,于是在网上找了一个sm4加密的代码(https://blog.csdn.net/songdawww/article/details/79112548),稍加修改即可得到正确答案(将源代码主函数的ecb解密留下,将密钥和密文放入即可)
key_data = [13, 204, 99, 177, 254, 41, 198, 163, 201, 226, 56, 214, 192, 194, 98, 104]
iv_data = [0x5a]*16
en_data=[46, 48, 220, 156, 184, 218, 57, 13, 246, 91, 1, 63, 60, 67, 105, 64, 149, 240, 217, 77, 107, 49, 222, 61, 155, 225, 231, 196, 167, 121, 9, 16, 60, 182, 65, 101, 39, 253, 250, 224, 9, 204, 154, 122, 206, 43, 97, 59]
sm4_d.sm4_set_key(key_data, DECRYPT)
de_data = sm4_d.sm4_crypt_ecb(en_data)
de_data_str = "".join([chr(x) for x in de_data])
print de_data_str![]()
crypto dp:
题目中我们可以拿到e,n,dp,c,这里dp=e^(-1)mod(p-1)。于是我们有m^(e*dp) mod p=m,即m^(e*dp)=k*p+m,于是我们有(m^(e*dp)) mod n=(k*p+m) mod n= k*p+m,这时我们有gcd(((m^(e*dp)) mod n)-m,n)=gcd(k*p,n)=p,即可正常将n分解
代码如下
import binascii
import gmpy2
e=65537
n=9637571466652899741848142654451413405801976834328667418509217149503238513830870985353918314633160277580591819016181785300521866901536670666234046521697590230079161867282389124998093526637796571100147052430445089605759722456767679930869250538932528092292071024877213105462554819256136145385237821098127348787416199401770954567019811050508888349297579329222552491826770225583983899834347983888473219771888063393354348613119521862989609112706536794212028369088219375364362615622092005578099889045473175051574207130932430162265994221914833343534531743589037146933738549770365029230545884239551015472122598634133661853901
dp=81339405704902517676022188908547543689627829453799865550091494842725439570571310071337729038516525539158092247771184675844795891671744082925462138427070614848951224652874430072917346702280925974595608822751382808802457160317381440319175601623719969138918927272712366710634393379149593082774688540571485214097
c=5971372776574706905158546698157178098706187597204981662036310534369575915776950962893790809274833462545672702278129839887482283641996814437707885716134279091994238891294614019371247451378504745748882207694219990495603397913371579808848136183106703158532870472345648247817132700604598385677497138485776569096958910782582696229046024695529762572289705021673895852985396416704278321332667281973074372362761992335826576550161390158761314769544548809326036026461123102509831887999493584436939086255411387879202594399181211724444617225689922628790388129032022982596393215038044861544602046137258904612792518629229736324827
# Random R
r = 2
# n = pq
p = gmpy2.gcd(n, pow(r, (e*dp), n) - r)
q = gmpy2.div(n, p)
print("p: %d" % p)
print("q: %d" % q)
# calculate d
phi = (p-1) * (q-1)
d = gmpy2.invert(e, phi)
print("phi: %d" % phi)
print("d: %d" % d)
# Calculate message
m = int(pow(c, d, n))
print("m: %d" % m)
# Convert int message to string
mHex = format(m, 'x')
print(mHex)
message = binascii.unhexlify(mHex).decode("utf-8")
print(message)re src_leak:
我们查看源码发现我们需要符合func3< func2
sum=0;
for i in xrange(1,963):
sum=sum+(2*i+1)
print sum我们将这范围的数字代入 func3< func2
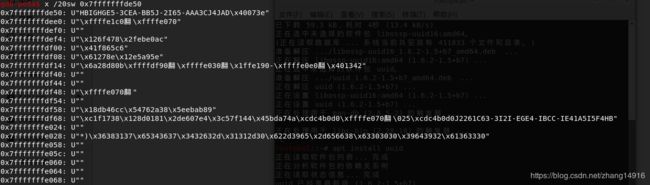
接下来我们需要知道在0 re flat 题目提示uuid,所以我们输入flag{uuid},即可到uuid的检查,逐步执行uuid检查程序,我们发现在程序中做了如下的更改,他将原先的uuid中的数字“0123456789”转为“ABCDEFGHIJ",将字母abcdef转为数字”123456“,然后我们可以在执行的时候观察栈我们会发现我们的uuid加密后得到的密文和最后要检验的密文,所以我们只需要将密文解密即可得到答案 dict1={"A":"0","B":"1","C":"2","D":"3","E":"4","F":"5","G":"6","H":"7","I":"8","J":"9","1":"a","2":"b","3":"c","4":"d","5":"e","6":"f"}
cipher="J2261C63-3I2I-EGE4-IBCC-IE41A5I5F4HB"
message=""
for i in cipher:
if dict1.has_key(i):
message=message+dict1[i]
else:
message=message+i
print message