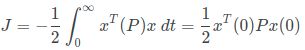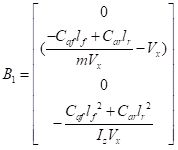自动驾驶(七十二)---------LQR控制算法
之前有写过MPC的控制算法,主要介绍的也是理论部分,在实际使用过程中发现C++没有高效的优化方法,类似python中的cvxpy的库,所以想绕过去,研究一下LQR控制算法。
1. 控制系统
这里我们先介绍常用的控制系统逻辑:
假设我们现在状态是x0,我们有状态方程 : 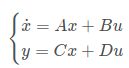 (u为控制矩阵)
(u为控制矩阵)
特别的,这里我们是对偏差建立方程,x是偏差的状态,优化的目的是x=0,针对![]() 我们通过一些假设可以得到详细的方程,这里我直接先给出
我们通过一些假设可以得到详细的方程,这里我直接先给出![]() 其中,
其中,
详细的推导有兴趣可以看最后。
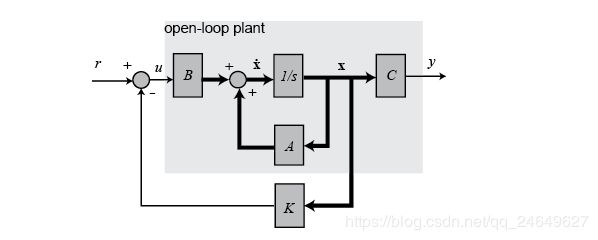
再假设有一个反馈控制器: ![]() 这里很重要,可以认为是当前的控制量是通过当前的状态量计算出来的。
这里很重要,可以认为是当前的控制量是通过当前的状态量计算出来的。
通过这套方法,我们就能得到一个稳定的系统 : ![]()
当然这是基本的理论,再进一步,我们就会思考,通过这些控制量作为自变量,再设计一个代价函数,来优化这些控制量?
2. LQR控制算法
讲到这里就很自然引出LQR了,首先的问题代价函数是什么?这里我直接给出:
其中x为状态量,u为控制量,Q为状态权重矩阵,R为控制权重矩阵。
特别的x和u中取值有正有负,所以需要平方和最小,在矩阵中没有平方,这里我们采用转置乘以本身的做法模拟矩阵的平方,如x^T*x 。这里状态量x和控制量u都是多维向量,上式计算的结果是一个标量。
其实我们可以把![]() 看作是
看作是![]() 的多维扩展表达式,这里我们需要Q为半正定,就是希望Q能起到a≥0的效果,R为正定矩阵就是希望矩阵R能够起到a>0的效果。
的多维扩展表达式,这里我们需要Q为半正定,就是希望Q能起到a≥0的效果,R为正定矩阵就是希望矩阵R能够起到a>0的效果。
一般的我们认为状态量x为:横向偏差、横向变化率、角度偏差、角度变化率。Q为我们提前标定的对角矩阵,标定值对应以上不同维度的权重,也可以为非对角矩阵,考虑不同维度之间的相互关系。
控制向量u为:前轮转角、加速度。同样的R也为提前标定的对角矩阵。也可以考虑相互关系。
我的理解是Q11选取较大的值,会让x1很快到0;另外一方面,加大R的值,会使得对应的控制量减小,控制器执行更少的动作,意味着系统的状态衰减将变慢。所以要综合看具体的实际应用场景来调节,鱼和熊掌不可兼得。建议在不同场景下采用不同的参数。
3. 公式求解
有了上面的优化目标后,就是如何求解最优的控制量了。下面我们先进行一些转换:
1. 将u=−Kx代入代价函数后: ![]() ,u=−Kx即我们认为当前的控制量可以通过当前的状态量计算出来。如果我们能计算出-K就很简单了,可以直接套出控制量。
,u=−Kx即我们认为当前的控制量可以通过当前的状态量计算出来。如果我们能计算出-K就很简单了,可以直接套出控制量。
2. 假设纯在一个常量矩阵P使得, ![]() ,这里就直接这么假设,接着往下看,有需要深入的同学可以看后面详细推导,总之,在等式成立的情况下,J取最小值,达到我们的优化目标。
,这里就直接这么假设,接着往下看,有需要深入的同学可以看后面详细推导,总之,在等式成立的情况下,J取最小值,达到我们的优化目标。
4. 把2中的方程微分展开:![]()
通过矩阵得知上式要想有解只有中间部分为零,即:![]()
6. 把![]() 代入上式:
代入上式:![]()
整理得到: ![]()
7. 这里我们再令 ![]() 这里需要思考一下,为什么可以这样假设,凑出结果?为了不增加复杂度,把这里的推导我放在最后,感兴趣的朋友可以继续研究。总之 在上面等式成立的情况下,可以得到
这里需要思考一下,为什么可以这样假设,凑出结果?为了不增加复杂度,把这里的推导我放在最后,感兴趣的朋友可以继续研究。总之 在上面等式成立的情况下,可以得到![]() 。
。
代入:![]()
整理得到: ![]() ,得到这一步就很简单了,式中A、B、Q、R都是已知量,很容易就能计算出P的结果。
,得到这一步就很简单了,式中A、B、Q、R都是已知量,很容易就能计算出P的结果。
8. 计算出P再通过![]() 就可以计算出K,也就是达到了我们一开始的目标,轻松得到当前的控制量。
就可以计算出K,也就是达到了我们一开始的目标,轻松得到当前的控制量。
4. MPC与LQR比较
首先,LQR的研究对象是现代控制理论中的状态空间方程给出的线性系统,而MPC的研究对象可以是线性系统,也可以是非线性系统。不过现在很多的做法都是将非线性系统线性化,然后进行相关计算,具体要根据自己的工程情况来确定哪种方式比较好,比如之前做MPC的时候,线控车底层速度控制接口就是加速度,那就没必要根据IMU再套嵌个一层PID。
其次,既然是优化问题,那就离不开目标函数的设计,LQR的目标函数在上面已经有描述,MPC的目标函数,多数都是多个优化目标乘以不同权重然后求和的方式。虽然方式不同,不过都是对达到控制目标的代价累计。
最后,工作时域上的不同,LQR的计算针对同一工作时域,在一个控制周期内,LQR只计算一次,并将此次计算出的最优解下发给控制器即可;而MPC是滚动优化的,计算未来一段时间内,每个采样周期都会经过计算,得出一组控制序列,但是只将第一个控制值下发给控制器。
对于LQR所有的理论部分都介绍完毕,下面是之前的一些公司推导部分,有兴趣的可以阅读:
1. 运动学模型的推导
在小角度偏角的情况下有,轮胎的侧向力与轮胎的偏离角成正比. ,分别为前、后轮的侧偏刚度:![]()
![]() 横摆角角度偏差;
横摆角角度偏差;
![]() (8)横向偏差变化率
(8)横向偏差变化率
车辆模型的连续状态空间方程 ![]()
状态变量X的选择分别为横向偏差、横向偏差变化率,横摆角角度偏差,横摆角角度偏差变化率。控制量u为前轮偏角。
选择合适的状态变量后得到A,B,B1,B2矩阵分别如下
由于![]() 只对横摆角角度偏差变化率的导数产生影响,在横向控制中主要是控制横向偏差、横向偏差变化率,横摆角角度偏差,横摆角角度偏差变化率,因而忽略了公式中
只对横摆角角度偏差变化率的导数产生影响,在横向控制中主要是控制横向偏差、横向偏差变化率,横摆角角度偏差,横摆角角度偏差变化率,因而忽略了公式中![]() 的
的![]() 项。车辆系统的状态空间方程表示为
项。车辆系统的状态空间方程表示为![]() (10)
(10)
2. 最优化目标的等价条件
首先控制理论是一门学科,我建议其他专业同学,直接使用以上的结论,如果你非要想完全理解,你需要具备以下知识:泛函极值、哈密尔顿方程、正则方程、无约束条件泛函、变分法、拉格朗日方程、黎卡提微分方程、控制域、欧拉方程、等周长积分方程......等等知识点。如果说你都具备,欢迎你往下看,不然你还是多看几遍上面把。
3.对于 ![]() 的推导
的推导
在前面的公式中,我们假设![]() ,到底这部分假设有没有数学推导呢?
,到底这部分假设有没有数学推导呢?
回到之前的公式: ![]() ,
,
同时我们知道R是正定对称矩阵,则一定存在一个矩阵M使得:![]() ,因为R的每一项大于零,M也为对角矩阵,数字为其平方根。
,因为R的每一项大于零,M也为对角矩阵,数字为其平方根。
代入R得到: