详解堆

堆的定义

①堆是一颗完全二叉树
②堆中的任意一个节点大于（或小于）它所有子树的节点的值。

堆的分类

①大顶堆：如果堆中任意节点的值大于等于子树的任意节点
②小顶堆：如果堆中任意节点的值小于等于子树的任意节点
大顶堆：
小顶堆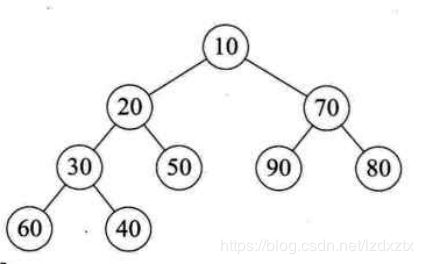

堆的存储

堆是一颗存在数组里的二叉树，若从下标1开始存储数据元素，则它的左儿子为Data[2i],右儿子为 Data[2i+1],若从下标0开始存储数据元素，则它的左儿子为Data[2i+1],右儿子为Data[2i+2]。

堆的相关操作

为了代码的标准性，笔者参考了mooc上浙江大学的代码

以大顶堆为例，且从1开始存储元素

申请空间

typedef struct Hnode* Heap;
struct Hnode
{
    int* Data;
    int  Size;//为堆当前的元素数目
    int max_size;//能放的最大元素数量
};
Heap Create_Heap(int max_size)
{
    Heap H=(Heap)malloc(sizeof(struct Hnode));
    H->Data=(int*)malloc(sizeof(int)*max_size);//申请空间，建立数组
    H->Size=0;//现有元素个数为0
    H->max_size=max_size-1;//因为0不存储数据元素，所以最多有max_size-1个
    return H;
}

插入

假设堆中现在有n个元素，现在往堆中插入元素x。
①先把元素放在n+1的位置，然后与它的父节点比较，如果父节点的值小于x，那么说明x比父节点的值“更有资格”做在父亲的位置，所以他们要发生交换，直到x的值小于父节点的值。
代码如下：

bool Insert(Heap H,int x)
{
    if(H->Size==H->max_size)
    {
        printf("堆满\n");//判断堆是否满
        return false;
    }
    else{
        int i=++H->Size;//i为x的待插入位置，一定是++H->Size,不是H->Size++
        while((i>=2)&&(H->Data[i/2]<x))//i>=2 是为了让它有父节点 后一个条件是x能否与父节点交换数据
        {
            H->Data[i]=H->Data[i/2];
            i/=2;
        }
        H->Data[i]=x;//i为x的最终位置
        return true;
    }
}

删除

①大顶堆的根节点肯定是最大的，（堆在c++中貌似跟优先级队列很像），所以每次把Data[1]拿走，然后让最后一个元素x放在Data[1]。
②然后对剩下的n-1个元素进行调整，重新调整成为一个堆。
代码如下：

int Delete(Heap H)
{
    if(H->Size==0)
    {
        printf("堆空");
        return -1;
    }
    else{
        int max_num=H->Data[1];//最后返回最大值
        int x=H->Data[H->Size--];//把最后的一个元素拿到第一个位置，同时元素个数减一
        int parent,child;//parent为x待放位置
        for(parent=1;parent*2<=H->Size;parent=child)
        {
            child=2*parent;
            if(child!=H->Size&&H->Data[child]<H->Data[child+1])//第一个条件是为了保证x有右儿子，第二个是取左右儿子中较大的一者
                child++;
            if(x>=H->Data[child])break;//符合堆的性质，不用交换
            else H->Data[parent]=H->Data[child];//否则，“不配”做在父亲的位置上，与儿子交换
        }
        H->Data[parent]=x;//x找打合适的位置
        return max_num;//返回最大值
    }
}

如何建堆？

建堆有两种操作：
①插入建堆。
每次读入一个节点，进行一次插入操作：

 for(int i=1;i<=n;i++)
    {
        scanf("%d",&x);
        Insert(H,x);
    }

此算法的时间复杂度为nlog(n)
②调整建堆
一次性读入所有数据，然后从第一个含有儿子节点的节点开始调整。
即从(H->Size)/2开始，到1结束，这时需要到一个调整函数，此函数其实在堆的删除操作中用过，即从上往下过滤。

void Prec_Down(Heap H,int i,int n)//x元素现在堆中的位置为i,此函数为x找到一个合适的位置，使之符合堆的特性，前n个元素需要调整
{
    int x=H->Data[i];
    int parent,child;
    for(parent=i;parent*2<=n;parent=child)
    {
        child=2*parent;
        if(child!=n&&H->Data[child]<H->Data[child+1])
            child++;
        if(x>=H->Data[child])break;
        else H->Data[parent]=H->Data[child];
    }
    H->Data[parent]=x;
}

调整建堆代码：

for(int i=1;i<=n;i++)
    {
        scanf("%d",&H->Data[i]);
    }
    H->Size=n;//要手动设置！
    for(int i=H->Size/2;i>=1;i--)
        Prec_Down(H,i,H->Size);

此方法建堆的时间复杂度为O(n)

堆排序

升序一般建立大顶堆，降序一般建立小顶堆
代码：

void Heap_Sort(Heap H)
{
    for(int i=H->Size;i>1;i--)
    {
        swap(H->Data[1],H->Data[i]);
        Prec_Down(H,1,i-1);
    }
}