基于对偶四元数的姿轨耦合动力学模型
基于对偶四元数的航天器姿轨耦合建模
对偶四元数能一体化描述空间刚体转动和平动,基于对偶四元数建立航天器相对运动的姿轨耦合动力学模型。对偶四元数表示的动力学模型形式简洁,具有明确的物理意义,与四元数描述的相对姿态动力学模型形式相似,继承了四元数不含三角运算、无奇异性的优点。
研究现状
传统的航天器六自由度建模多采用“独立-耦合”方法,即用不同的数学方法描述航天器姿态运动和轨道运动,然后考虑姿轨耦合因素,联立实现航天器姿轨一体化建模过程。由于所建立的姿轨模型中姿态和轨道参数描述不统一,模型求解过程比较困难,这不是真正的姿轨一体化模型。
传统的航天器六自由度相对运动模型实际上是一种“伪六自由度模型”,忽略了相对姿态运动和相对位置运动之间的耦合,本质上仍为两个三自由度分离模型。为了更加贴合航天器姿轨一体化控制任务的实际需求,六自由度运动描述方法建立姿轨耦合运动学和动力学模型。
对偶四元数不仅可以描述航天器相对姿态运动,还可以同时且协同地描述相对位置变化。基于误差对偶四元数建立的航天器姿态和轨道相对运动学和动力学模型与基于误差四元数的航天器相对姿态运动模型具有相同的形式。
在同一数学框架内建立航天器的姿态运动和轨道运动模型,才是实现姿轨一体化的正确方法。
邹晖:几何代数的方法。
坐标系定义
惯性坐标系 O i x i y i z i O_{i}x_{i}y_{i}z_{i} Oixiyizi,原点为地心,简称I系
追踪航天器本体坐标系 O b x b y b z b O_{b}x_{b}y_{b}z_{b} Obxbybzb,原点为追踪航天器质心 O b O_{b} Ob,简称B系。
目标航天器本体坐标系 O t x t y t z t O_{t}x_{t}y_{t}z_{t} Otxtytzt,原点为目标航天器质心 O t O_{t} Ot,简称T系。
期望坐标系 O d x d y d z d O_dx_dy_dz_d Odxdydzd,根据任务需求而定义,简称D系。交会对接任务中,D系与I系保持相对静止;绕飞和监视任务中,D系相对I系实时变化。D系的引入增加了控制目标设计的灵活性。
四元数
四元数的定义、运算法则和物理含义
四元数的基本定义:
q = q 0 + q 1 i ⃗ + q 2 j ⃗ + q 3 k ⃗ = q 0 + q ⃗ q = q_{0} + q_{1}\vec{i} + q_{2}\vec{j} + q_{3}\vec{k} = q_{0} + \vec{q} q=q0+q1i+q2j+q3k=q0+q
其中, q 0 q_{0} q0是四元数的标量部分(Scalar Part), q ⃗ \vec{q} q是四元数的矢量部分(Vector Part)。也可以表示为列向量的形式 q = ( q 0 , q ⃗ ) q = (q_{0},\vec{q}) q=(q0,q)。
四元数乘法:
令 q = η + ξ 1 i ⃗ + ξ 2 j ⃗ + ξ 3 k ⃗ = [ η , ξ ⃗ T ] T q = \eta + \xi_1 \vec i + \xi_2 \vec j + \xi_3 \vec k = [\eta, \vec{\xi}^T]^T q=η+ξ1i+ξ2j+ξ3k=[η,ξT]T,其中, ξ ⃗ = [ ξ 1 , ξ 2 , ξ 3 ] T \vec{\xi} = [\xi_1, \xi_2, \xi_3]^T ξ=[ξ1,ξ2,ξ3]T,那么 q 1 = [ η 1 , ξ ⃗ 1 T ] q_1 = [\eta_1, \vec{\xi}_1^T] q1=[η1,ξ1T], q 2 = [ η 2 , ξ ⃗ 2 T ] q_2 = [\eta_2, \vec{\xi}_2^T] q2=[η2,ξ2T]。则其乘法运算法则为:
q 1 ⊗ q 2 = [ η 1 η 2 − ξ ⃗ 1 T ξ ⃗ 2 , ( η 1 ξ ⃗ 2 + η 2 ξ ⃗ 1 + ξ ⃗ 1 × ξ ⃗ 2 ) ] T = [ q 1 ] ⊗ q 2 q_1 \otimes q_2 = [\eta_1 \eta_2 - \vec{\xi}_1^T \vec{\xi}_2, (\eta_1 \vec{\xi}_2 + \eta_2 \vec{\xi}_1 + \vec{\xi}_1 \times \vec{\xi}_2)]^T = [q_1]_{\otimes}q_2 q1⊗q2=[η1η2−ξ1Tξ2,(η1ξ2+η2ξ1+ξ1×ξ2)]T=[q1]⊗q2
其中, [ q 1 ] ⊗ [q_1]_{\otimes} [q1]⊗表示一个参数矩阵,定义为:
[ q 1 ] ⊗ = [ η − ξ ⃗ 2 ξ ⃗ η I 3 × 3 + S ( ξ ⃗ ) ] [q_1]_{\otimes} = \left[ \begin{matrix} \eta & -\vec{\xi}^2 \\ \vec{\xi} & \eta {\bf{I}}_{3 \times 3} + S(\vec{\xi}) \end{matrix} \right] [q1]⊗=[ηξ−ξ2ηI3×3+S(ξ)]
参数矩阵 S ( ⋅ ) S(\cdot) S(⋅)表示对应三维向量的反对称矩阵,以 ξ ⃗ \vec \xi ξ为例,其表达式为:
S ( ξ ⃗ ) = [ 0 − ξ 3 ξ 2 ξ 3 0 − ξ 1 − ξ 2 ξ 1 0 ] S(\vec \xi) = \left[ \begin{matrix} 0 & -\xi_3 & \xi_2 \\ \xi_3 & 0 & -\xi_1 \\ -\xi_2 & \xi_1 & 0 \end{matrix} \right] S(ξ)=⎣⎡0ξ3−ξ2−ξ30ξ1ξ2−ξ10⎦⎤
欧拉转动定理指出,在三维空间中,一个刚体在位移时,若刚体上至少有某一点保持固定不动,则此位移等价于绕着通过这一固定点的某固定轴的旋转。记这一固定轴(欧拉旋转轴)的单位矢量方向为 e ⃗ \vec{e} e,并以 θ \theta θ表示等价旋转运动的旋转角(欧拉角),则这一等价的旋转运动可由一个单位四元数 q = [ η , ξ ⃗ T ] T q = [\eta, \vec{\xi}^T]^T q=[η,ξT]T表示,且 η \eta η和 ξ ⃗ \vec{\xi} ξ满足:
η = cos ( θ 2 ) ξ ⃗ = e ⃗ sin ( θ 2 ) \eta = \cos(\frac{\theta}{2}) \\ \vec{\xi} = \vec{e} \sin(\frac{\theta}{2}) η=cos(2θ)ξ=esin(2θ)
定性来讲, η \eta η描述了欧拉角的大小,而 ξ ⃗ \vec{\xi} ξ描述了欧拉旋转轴的方向,且为单位四元数。
单位四元数既可以描述两坐标系的相对位姿关系,也可以表达某一向量在不同坐标系中的投影映射关系。
基于四元数的航天器姿态运动学模型
见“基于误差四元数的相对姿态运动学模型”。
基于四元数的航天器姿态动力学学模型
见“基于误差四元数的相对姿态动力学模型”。
基于误差四元数的相对姿态运动学模型
追踪器的姿态运动学方程为:
q ˙ B I = 1 2 q B I ⊗ ω ⃗ B I B = 1 2 ω ⃗ B I I ⊗ q B I \dot{q}_{BI} = \frac{1}{2} q_{BI} \otimes \vec{\omega}_{BI}^B = \frac{1}{2} \vec{\omega}_{BI}^I \otimes q_{BI} q˙BI=21qBI⊗ωBIB=21ωBII⊗qBI
目标器的姿态运动学方程为:
q ˙ T I = 1 2 q T I ⊗ ω ⃗ T I B = 1 2 ω ⃗ T I I ⊗ q T I \dot{q}_{TI} = \frac{1}{2} q_{TI} \otimes \vec{\omega}_{TI}^B = \frac{1}{2} \vec{\omega}_{TI}^I \otimes q_{TI} q˙TI=21qTI⊗ωTIB=21ωTII⊗qTI
其中, ω ⃗ B I B \vec{\omega}_{BI}^B ωBIB表示追踪器相对于I系的姿态角速度在B系下的分量, ω ⃗ T I T \vec{\omega}_{TI}^T ωTIT表示目标相对于I系的姿态角速度在T系下的分量。
定义误差四元数为:
q B T = q T I ∗ ⊗ q B I q_{BT} = q_{TI}^* \otimes q_{BI} qBT=qTI∗⊗qBI
则相对姿态运动学方程为:
q ˙ B T = 1 2 q B T ⊗ ω ⃗ B T T = 1 2 ω ⃗ B T T ⊗ q B T \dot{q}_{BT} = \frac{1}{2} q_{BT} \otimes \vec{\omega}_{BT}^T = \frac{1}{2} \vec{\omega}_{BT}^T \otimes q_{BT} q˙BT=21qBT⊗ωBTT=21ωBTT⊗qBT
其中,相对角速度在B系和T系下的分量分别为:
ω ⃗ B T B = ω ⃗ B I B − ω ⃗ T I B ω ⃗ B T T = ω ⃗ B I T − ω ⃗ T I T \vec{\omega}_{BT}^B = \vec{\omega}_{BI}^B - \vec{\omega}_{TI}^B \\ \vec{\omega}_{BT}^T = \vec{\omega}_{BI}^T - \vec{\omega}_{TI}^T ωBTB=ωBIB−ωTIBωBTT=ωBIT−ωTIT
基于误差四元数的相对姿态动力学模型
追踪器姿态动力学方程:
J ˉ ω ⃗ ˙ B I B + ω ⃗ B I B × ( J ˉ ω ⃗ B I B ) = T B \bar{J} \dot{\vec{\omega}}_{BI}^{B} + \vec{\omega}_{BI}^{B} \times (\bar{J} \vec{\omega}_{BI}^{B}) = T^{B} Jˉω˙BIB+ωBIB×(JˉωBIB)=TB
目标器姿态动力学方程在追踪器本体坐标系B系下的表达式为(我猜):
J ˉ ω ⃗ ˙ T I B + ω ⃗ T I B × ( J ˉ ω ⃗ T I B ) = T B \bar{J} \dot{\vec{\omega}}_{TI}^{B} + \vec{\omega}_{TI}^{B} \times (\bar{J} \vec{\omega}_{TI}^{B}) = T^{B} Jˉω˙TIB+ωTIB×(JˉωTIB)=TB
其中, J ˉ \bar{J} Jˉ表示本体系下追踪器or目标转动惯量矩阵, T B T^{B} TB表示作用于追踪器或目标的总力矩。
将 ω ⃗ ˙ B I B = ω ⃗ ˙ B T B + ω ⃗ ˙ T I B \dot{\vec{\omega}}_{BI}^B = \dot{\vec{\omega}}_{BT}^B + \dot{\vec{\omega}}_{TI}^B ω˙BIB=ω˙BTB+ω˙TIB代入到追踪器姿态动力学方程中,可得相对姿态动力学方程为:
ω ⃗ ˙ B T B = J − 1 ( T B − ( ω ⃗ B T B + ω ⃗ T I B ) × ( J ( ω ⃗ B T B + ω ⃗ T I B ) ) ) − q B T ∗ × ω ⃗ ˙ T I T × q B T − ω ⃗ T I B × ω ⃗ B T B \dot{\vec{\omega}}_{BT}^B = J^{-1}(T^B - (\vec{\omega}_{BT}^B + \vec{\omega}_{TI}^B) \times (J(\vec{\omega}_{BT}^B + \vec{\omega}_{TI}^B))) - q_{BT}^* \times \dot{\vec{\omega}}_{TI}^T \times q_{BT} - \vec{\omega}_{TI}^B \times \vec{\omega}_{BT}^B ω˙BTB=J−1(TB−(ωBTB+ωTIB)×(J(ωBTB+ωTIB)))−qBT∗×ω˙TIT×qBT−ωTIB×ωBTB
J J J与 J ˉ \bar{J} Jˉ的形式如下:
J = [ 1 0 1 × 3 0 3 × 1 J ˉ ] , J ˉ = [ J 11 J 12 J 13 J 21 J 22 J 23 J 31 J 32 J 33 ] J = \left[ \begin{matrix} 1 & 0_{1 \times 3} \\ 0_{3 \times 1} & \bar J \end{matrix} \right], \bar{J} = \left[ \begin{matrix} J_{11} & J_{12} & J_{13} \\ J_{21} & J_{22} & J_{23} \\ J_{31} & J_{32} & J_{33} \\ \end{matrix} \right] J=[103×101×3Jˉ],Jˉ=⎣⎡J11J21J31J12J22J32J13J23J33⎦⎤
对偶数和对偶四元数
对偶数的定义和运算法则
对偶数(Dual Number)的定义:
z ^ = z + ϵ z ′ \hat{z} = z + \epsilon z' z^=z+ϵz′
其中, z z z和 z ′ z' z′是实数, z z z称作对偶数的实部, z ′ z' z′称为对偶数的对偶部, ϵ \epsilon ϵ称为对偶单位,可以理解为 ϵ = [ 0 0 x 0 ] \epsilon = \left[ \begin{matrix} 0 & 0 \\ x & 0 \end{matrix} \right] ϵ=[0x00],有 ϵ 2 = 0 {\epsilon}^2 = 0 ϵ2=0和 ϵ ≠ 0 \epsilon \neq 0 ϵ=0成立。
如果对偶数的实部和对偶部都是向量,即 v ⃗ ^ = v ⃗ + ϵ v ⃗ ′ \hat{\vec{v}} = \vec{v} + \epsilon \vec{v}' v^=v+ϵv′,则该对偶数称为对偶向量,可以理解为实部和对偶部都是向量的的对偶数,也可以理解为元素为对偶数的向量。类似的,对偶矩阵和对偶四元数都可以这么理解。
如果对偶向量实部 v ⃗ \vec{v} v是定位矢量,即与参考点的选择无关,对偶部 v ⃗ ′ \vec{v}' v′为自由矢量,这样的对偶向量称为“旋量”,后面航天器动力学中的对偶速度矢量、对偶力矢量都可以看做旋量。
对偶四元数的定义和物理含义
对偶四元数的定义和运算法则
对偶四元数(Dual Quaternions)是对偶数和四元数在多维空间相结合的产物,可以理解为元素为四元数的对偶数,也可以理解为元素为对偶数的四元数。四元数只能表示3D旋转,对偶数只能表示平移,对偶四元数集成了两者的共同特性,从而能统一的表示旋转和平移。形式如下:
q ^ = [ η ^ , ξ ⃗ ^ ] = [ η + ϵ η ′ , ξ ⃗ + ϵ ξ ⃗ ′ ] = q r + ϵ q d = η + ξ 1 i ⃗ + ξ 2 j ⃗ + ξ 3 k ⃗ + ϵ ( η ′ + ξ ′ 1 i ⃗ + ξ ′ 2 j ⃗ + ξ ′ 3 k ⃗ ) = [ η + ϵ η ′ , ξ 1 + ϵ ξ 1 ′ , ξ 2 + ϵ ξ 2 ′ , ξ 3 + ϵ ξ 3 ′ ] \hat{q} = [\hat{{\eta}}, \hat{\vec{\xi}}] = [\eta + \epsilon {\eta}', \vec{\xi} + \epsilon \vec{\xi}'] = q_r + \epsilon q_d \\ \ \ \, = {\eta} + {\xi}_1 \vec{i} + {\xi}_2 \vec{j} + {\xi}_3 \vec{k} + \epsilon ({\eta'} + {\xi'}_1 \vec{i} + {\xi'}_2 \vec{j} + {\xi'}_3 \vec{k}) \\ = [\eta + \epsilon {\eta}', \xi_1 + \epsilon {\xi_1}', \xi_2 + \epsilon {\xi_2}', \xi_3 + \epsilon {\xi_3}'] \ \ \ \ \ \ \ \ \ \ \ \ \ q^=[η^,ξ^]=[η+ϵη′,ξ+ϵξ′]=qr+ϵqd =η+ξ1i+ξ2j+ξ3k+ϵ(η′+ξ′1i+ξ′2j+ξ′3k)=[η+ϵη′,ξ1+ϵξ1′,ξ2+ϵξ2′,ξ3+ϵξ3′]
其中, η ⃗ ^ \hat{\vec{\eta}} η^和 ξ ⃗ ^ \hat{\vec{\xi}} ξ^为对偶数和对偶向量, q r q_r qr和 q d q_d qd是普通的四元数,分别称为对偶四元数的实部和对偶部。
对偶四元数的乘法运算法则:
q ^ 1 ⊗ q ^ 2 = [ η ^ 1 η ^ 2 − ξ ⃗ ^ 1 T ξ ⃗ ^ 2 , ( η ^ 1 ξ ⃗ ^ 2 + η ^ 2 ξ ⃗ ^ 1 + ξ ⃗ ^ 1 × ξ ⃗ ^ 2 ) T ] T = ( q 1 r ⊗ q 2 r ) + ϵ ( q 1 r ⊗ q 2 d + q 1 d ⊗ q 2 r ) = [ q 1 ] ⊗ q 2 \hat q_1 \otimes \hat q_2 = [\hat\eta_1 \hat\eta_2 - \hat{\vec{\xi}}_1^T \hat{\vec{\xi}}_2, (\hat \eta_1 \hat{\vec{\xi}}_2 + \hat\eta_2 \hat{\vec{\xi}}_1 + \hat{\vec{\xi}}_1 \times \hat{\vec{\xi}}_2)^T]^T = (q_{1r} \otimes q_{2r}) + \epsilon (q_{1r} \otimes q_{2d} + q_{1d} \otimes q_{2r}) \\ = [q_1]_{\otimes} q_2 q^1⊗q^2=[η^1η^2−ξ^1Tξ^2,(η^1ξ^2+η^2ξ^1+ξ^1×ξ^2)T]T=(q1r⊗q2r)+ϵ(q1r⊗q2d+q1d⊗q2r)=[q1]⊗q2
对偶四元数的物理解释
Chasles定理:任何一般性刚体运动都可以通过绕某个轴的旋转和沿相同轴的平移实现。这种旋转和平移的组合很像是一种螺旋式的运动。
两坐标系之间的螺旋运动变换如下图所示, n ⃗ ^ \hat{\vec{n}} n^、 d d d、 θ \theta θ分别为螺旋轴、螺距和转角。类似于单位四元数可以描述姿态运动,单位对偶四元数可以用来同时描述坐标系的平动和转动。单位四元数 q B I q_{BI} qBI的几何意义为一个大圆弧矢量,类似的,单位对偶四元数 q ^ B I \hat{q}_{BI} q^BI的几何意义是一个螺旋弧矢量,可以看做是四元数和大圆法线矢量的合成。 q ^ B I \hat{q}_{BI} q^BI可以写为如下形式:
q ^ B I = [ cos ( θ ^ 2 ) , sin ( θ ^ 2 ) n ⃗ ^ ] , θ ^ = θ + ϵ d \hat{q}_{BI} = [\cos{(\frac{\hat{\theta}}{2})}, \sin{(\frac{\hat{\theta}}{2})} \hat{\vec{n}}], \hat{\theta} = \theta + \epsilon d q^BI=[cos(2θ^),sin(2θ^)n^],θ^=θ+ϵd
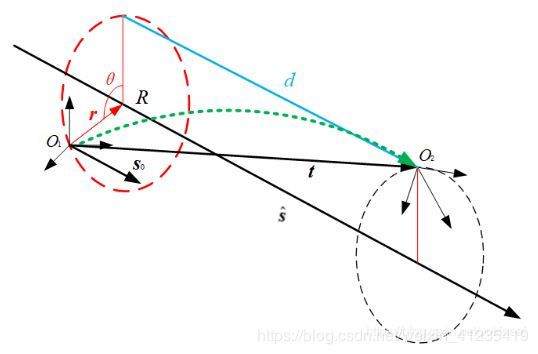
坐标系I到坐标系B的运动可以先转动 q B I q_{BI} qBI再平动 r B I B r_{BI}^{B} rBIB得到,也可以先平动 r B I B r_{BI}^{B} rBIB再转动 q B I q_{BI} qBI得到。空间暜吕克直线在两坐标系中的表达分别为 l ⃗ ^ I = l ⃗ I + ϵ m ⃗ I \hat{\vec{l}}^I = \vec{l}^I + \epsilon \vec{m}^I l^I=lI+ϵmI和 l ⃗ ^ B = l ⃗ B + ϵ m ⃗ B \hat{\vec{l}}^B = \vec{l}^B + \epsilon \vec{m}^B l^B=lB+ϵmB,可知 l ⃗ B = q B I ∗ ⊗ l ⃗ I ⊗ q B I {\vec{l}}^B = q_{BI}^* \otimes {\vec{l}}^I \otimes q_{BI} lB=qBI∗⊗lI⊗qBI。其中 l ⃗ I \vec{l}^I lI等矢量与四元数运算时标量部分按0的矢量四元数来处理。那么可以得到如下空间暜吕克直线的旋转公式,可以理解为同一对偶矢量在不同坐标系下的表示,也可以理解为同一坐标系中对偶矢量 l ⃗ ^ I \hat{\vec{l}}^I l^I进过六自由度运动到 l ⃗ ^ B \hat{\vec{l}}^B l^B。
l ⃗ ^ B = q ^ B I ∗ ⊗ l ⃗ ^ I ⊗ q ^ B I \hat{\vec{l}}^B = \hat q_{BI}^* \otimes \hat{\vec{l}}^I \otimes \hat q_{BI} l^B=q^BI∗⊗l^I⊗q^BI
其中, q ^ B I = q B I + ϵ q d \hat{q}_{BI} = q_{BI} + \epsilon q_d q^BI=qBI+ϵqd,且 q d = 1 2 q B I ⊗ r ⃗ B I B q_d = \frac{1}{2} q_{BI} \otimes \vec{r}_{BI}^B qd=21qBI⊗rBIB。
基于对偶四元数的航天器运动学模型
对于单航天器,轨道运动学和轨道动力学+姿态运动学和姿态动力学。轨道运动学和轨道动力学都是将航天器当成质点来研究的,因此不对动力学和运动学进行区分,统称为轨道动力学。
运动学是从几何的角度(不涉及物体本身的物理性质和加在物体上的力)描述和研究物体位置随时间的变化规律的力学分支。
动力学主要研究作用于物体上的力与物体运动的关系。动力学普遍定理包括动量定理、动量矩定理、动能定理,以及由这三个基本定理推导出的其他定理。
因此简单来讲,二体问题的运动方程即为单航天器轨道运动学模型,加上控制力后即为单航天器轨道动力学模型。而航天器相对轨道运动学模型也可以理解为无控制力(控制加速度)的C-W方程(T-H方程等),航天器相对轨道动力学模型即为有控制力(控制加速度)的C-W方程(T-H方程等)。
而航天器姿态运动学模型和姿态动力学模型就不能简单理解为有无控制力矩的问题(也可以这么理解?)。
坐标系I到坐标系B的运动可以先转动 q B I q_{BI} qBI再平动 r B I B r_{BI}^{B} rBIB得到,也可以先平动 r B I B r_{BI}^{B} rBIB再转动 q B I q_{BI} qBI得到。空间暜吕克直线在两坐标系中的表达分别为 l ⃗ ^ I = l ⃗ I + ϵ m ⃗ I \hat{\vec{l}}^I = \vec{l}^I + \epsilon \vec{m}^I l^I=lI+ϵmI和 l ⃗ ^ B = l ⃗ B + ϵ m ⃗ B \hat{\vec{l}}^B = \vec{l}^B + \epsilon \vec{m}^B l^B=lB+ϵmB,可知 l ⃗ B = q B I ∗ ∘ l ⃗ I ∘ q B I \vec{l}^B = q_{BI}^* \circ \vec{l}^I \circ q_{BI} lB=qBI∗∘lI∘qBI。其中 l ⃗ I \vec{l}^I lI等矢量与四元数运算时标量部分按0的矢量四元数来处理。
单位对偶四元数的八个量中独立变量只有六个,正好对应着刚体空间运动六自由度。对偶四元数的实部代表航天器姿态运动,对偶部代表航天器轨道运动。
基于对偶四元数的刚体空间运动学方程为:
q ^ ˙ B I = 1 2 q ^ B I ⊗ ω ⃗ ^ B I B = 1 2 ω ⃗ ^ B I I ⊗ q ^ B I \dot{\hat{q}}_{BI} = \frac{1}{2} \hat{q}_{BI} \otimes \hat {\vec{\omega}}_{BI}^B = \frac{1}{2} \hat {\vec{\omega}}_{BI}^I \otimes \hat{q}_{BI} q^˙BI=21q^BI⊗ω^BIB=21ω^BII⊗q^BI
从上式可以发现对偶四元数描述的刚体六自由度运动与四元数描述的刚体旋转运动由相似的表达式。
基于对偶四元数的航天器动力学模型
对偶四元数在描述旋量时,表示描述方向的实部不因参考点的选择而变化,而对偶部则与参考点的选择有关。
对偶形式的动力学方程为:
M ^ ω ⃗ ^ ˙ B I B = − ω ⃗ ^ B I B + F ^ B \hat{M} \dot{\hat{\vec\omega}}_{BI}^{B} = -\hat{\vec{\omega}}_{BI}^{B} + \hat{F}^B M^ω^˙BIB=−ω^BIB+F^B
其中, M ^ = m d d ϵ I 4 × 4 + ϵ J \hat{M} = m \frac{d}{d \epsilon} {\bf{I}}_{4 \times 4} + \epsilon J M^=mdϵdI4×4+ϵJ是追踪器对偶惯量阵, F ^ B = F B + ϵ T B = F ^ a + F ^ g + F ^ d \hat{F}^B = F^B + \epsilon T^B = \hat{F}_a + \hat{F}_g + \hat{F}_d F^B=FB+ϵTB=F^a+F^g+F^d是对偶力在B系下的分量,接下来的叙述省略上标 B B B。 F ^ a \hat{F}_a F^a实部为控制力,对偶部为控制力矩; F ^ g \hat{F}_g F^g实部为引力,对偶部为重力梯度力矩;对偶干扰力 F ^ d \hat{F}_d F^d在仿真时给出。
基于误差对偶四元数的相对姿轨耦合运动学模型
传统的航天器六自由度相对运动模型实际上式一种“伪六自由度模型”,忽略了相对姿态运动和相对位置运动之间的耦合,本质上仍为两个三自由度分离模型。为了更加贴合航天器姿轨一体化控制任务的实际需求,六自由度运动描述方法建立姿轨耦合运动学和动力学模型。对偶四元数可以同时且协同地描述相对位置变化。
坐标系B相对于坐标系T的误差对偶四元数定义为:
q ^ B T = q ^ T I ∗ ⊗ q ^ B I \hat{q}_{BT} = \hat{q}_{TI}^* \otimes \hat{q}_{BI} q^BT=q^TI∗⊗q^BI
显然,误差对偶四元数也是一个单位对偶四元数。 q ^ B T \hat{q}_{BT} q^BT满足如下表达式:
q ^ B T = q B T + ϵ 1 2 q B T ⊗ r B T B = q B T + ϵ 1 2 r B T T ⊗ q B T = q B T + ϵ q B T d \hat{q}_{BT} = q_{BT} + \epsilon \frac{1}{2} q_{BT} \otimes r_{BT}^B \\ = q_{BT} + \epsilon \frac{1}{2} r_{BT}^T \otimes q_{BT} = q_{BT} + \epsilon q_{BTd} q^BT=qBT+ϵ21qBT⊗rBTB=qBT+ϵ21rBTT⊗qBT=qBT+ϵqBTd
其中, r B T B r_{BT}^B rBTB和 r B T T r_{BT}^T rBTT分别为追踪器与目标的相对位置矢量在B系与T系的分量。
基于误差对偶四元数的姿轨耦合相对运动方程:
q ^ ˙ B T = 1 2 q ^ B T ⊗ ω ⃗ ^ B T B \dot{\hat q}_{BT} = \frac{1}{2} \hat{q}_{BT} \otimes \hat{\vec{\omega}}_{BT}^B q^˙BT=21q^BT⊗ω^BTB
其中 ω ⃗ ^ B T B \hat{\vec{\omega}}_{BT}^B ω^BTB为相对速度旋量在B系中的表达式。 ω ⃗ ^ B T B \hat{\vec{\omega}}_{BT}^B ω^BTB也可以写为如下形式:
ω ⃗ ^ B T B = ω ⃗ B T B + ϵ ( r ˙ B T B + ω ⃗ B T B × r B T B ) \hat{\vec{\omega}}_{BT}^B = \vec{\omega}_{BT}^B + \epsilon(\dot{r}_{BT}^B + \vec{\omega}_{BT}^B \times r_{BT}^B) ω^BTB=ωBTB+ϵ(r˙BTB+ωBTB×rBTB)
基于误差对偶四元数的相对姿轨耦合动力学模型
追踪航天器相对于目标航天器的姿轨耦合动力学方程为:
ω ⃗ ^ ˙ B T B = M ^ − 1 ( K ^ ω ⃗ ^ B T B + L ^ + F ^ ) \dot{\hat{\vec{\omega}}}_{BT}^B = \hat{M}^{-1} (\hat{K} {\hat{\vec{\omega}}}_{BT}^B + \hat L + \hat F) ω^˙BTB=M^−1(K^ω^BTB+L^+F^)
其中:
K ^ = K 1 d d ϵ + ϵ K 2 K 1 = − m ( ω ⃗ B T B + 2 ω ⃗ T I B ) × K 2 = ( J ( ω ⃗ B T B + ω ⃗ T I B ) ) × − ( ω ⃗ T I B ) × J − J ( ω ⃗ T I B ) × L ^ = L 1 + ϵ L 2 L 1 = − m q B T ∗ ⊗ v ˙ T I T ⊗ q B T − m ( q B T ∗ ⊗ ω ⃗ ˙ T I T ⊗ q B T ) × r ⃗ B T B − m ω ⃗ T I B × ( v T I B + ω ⃗ T I B × r ⃗ B T B ) L 2 = − J ( q B T ∗ ⊗ ω ⃗ ˙ T I T ⊗ q B T ) − ω ⃗ T I B ⊗ J ω ⃗ T I B \hat{K} = K_1 \frac{d}{d \epsilon} + \epsilon K_2 \\ K_1 = -m(\vec{\omega}_{BT}^B + 2 \vec{\omega}_{TI}^B)^{\times} \\ K_2 = (J(\vec{\omega}_{BT}^B + \vec{\omega}_{TI}^B))^{\times} - (\vec{\omega}_{TI}^B)^{\times}J - J (\vec{\omega}_{TI}^B)^{\times} \\ \hat L = L_1 + \epsilon L_2 \\ L_1 = -m q_{BT}^* \otimes \dot{v}_{TI}^T \otimes q_{BT} - m (q_{BT}^* \otimes \dot{\vec{\omega}}_{TI}^T \otimes q_{BT}) \times \vec{r}_{BT}^B - m \vec{\omega}_{TI}^B \times (v_{TI}^B + \vec{\omega}_{TI}^B \times \vec{r}_{BT}^B) \\ L_2 = -J(q_{BT}^* \otimes \dot{\vec{\omega}}_{TI}^T \otimes q_{BT}) - \vec{\omega}_{TI}^B \otimes J \vec{\omega}_{TI}^B K^=K1dϵd+ϵK2K1=−m(ωBTB+2ωTIB)×K2=(J(ωBTB+ωTIB))×−(ωTIB)×J−J(ωTIB)×L^=L1+ϵL2L1=−mqBT∗⊗v˙TIT⊗qBT−m(qBT∗⊗ω˙TIT⊗qBT)×rBTB−mωTIB×(vTIB+ωTIB×rBTB)L2=−J(qBT∗⊗ω˙TIT⊗qBT)−ωTIB⊗JωTIB
为方便控制器设计,可以将上式进一步展开。可以看出,轨道部分包含姿态参数,即表明轨道相对运动受到姿态相对运动的影响,耦合项是由动量在动坐标系中求导和航天器受力在不同坐标系中的表达带来的。同时,相对姿态运动方程中的 T g T_g Tg和 T d T_d Td与相对位置有关,但相对卫星轨道高度来说,相对位置是小量,可以忽略不计。
航天器相对运动控制中的问题
-
质量与惯量不确定性问题。
燃料消耗、载荷安装偏移、结构改变等因素将引起在轨航天器质量与惯量参数的变化。
-
线速度和角速度不可测问题。
-
运动约束问题。
由于受制于敏感元件、执行机构或其他载荷的各种限制,以及处于飞行安全和完成某些特殊任务的考虑,在轨航天器经常需要满足各类运动约束。
-
执行机构存在故障时的容错控制问题。
数值仿真
如何实现基于对偶四元数的航天器相对姿轨耦合运动学方程,需要搞懂每一个变量和系数的物理含义。
参考文献
- 杨嘉庚. 航天器相对运动姿轨耦合跟踪控制[D]. 2016. 哈尔滨工业大学.
- 吴锦杰. 航天器相对运动姿轨一体化动力学建模与控制技术研究[D]. 2013. 国防科技大学.
- 机器人学代数基础——对偶四元数与速度旋量(或运动螺旋)之间的转换.
- 董宏洋. 基于对偶四元数的航天器位姿一体化控制方法研究[D]. 2017. 哈尔滨工业大学.
- 孙俊. 在轨服务航天器位姿一体化规划与控制[D]. 2017. 哈尔滨工业大学.