本文作为金融量化分析的入门基础之一,手把手带领大家使用Python计算股票的收益率,重点展示如何利用Python对日收益率数据向月、年收益率转换,然后演示个股Alpha和Beta值的计算。
#先引入后面可能用到的包(package)
import pandas as pd
import numpy as np
from scipy import stats
import tushare as ts
import matplotlib.pyplot as plt
%matplotlib inline
#正常显示画图时出现的中文和负号
from pylab import mpl
mpl.rcParams['font.sans-serif']=['SimHei']
mpl.rcParams['axes.unicode_minus']=False
收益率转化
对日期进行处理,分别将日对数收益率转化为月和年收益率。主要有三个步骤:
(1)估计股票每日对数收益率;
(2)加总对数收益率到每月(年);
(3)将月(年)收益率转化为百分比收益率
stock='sh'
df=ts.get_k_data(stock,start='1990-12-20')
使用tushare中的get_k_data()得到的数据框索引是顺序数字,而不是日期序列,因此,为分析方面,需要进行变换,即使用“date”作为索引。
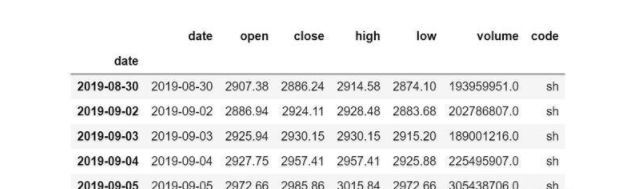
df.index=pd.to_datetime(df.date)
#del df['date'] #删掉该列
df.tail() #这时候可以看到索引已经是date了
遇到问题没人解答,小编创建了一个Python学习交流裙:五二八 三九七 六一七, 寻找有志同道合的小 伙伴,互帮互助,群里还有不错的学习视频教程和PDF电子书分享!
步骤一:计算对数收益率
#计算的时候第一个数成为缺失值,删掉
lograte=np.log(df.close/df.close.shift(1))[1:]
步骤二:加总对数收益率到每月
month=[]
index=lograte.index
for i in range(0,np.size(lograte)):
month.append(''.join([index[i].strftime("%Y"),index[i].strftime("%m")]))
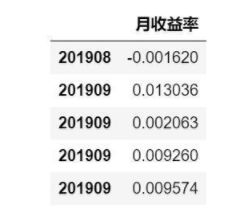
y=pd.DataFrame(lograte.values,month,columns=['月收益率'])
y.tail()
步骤三:将月(年)收益率转化为百分比收益率
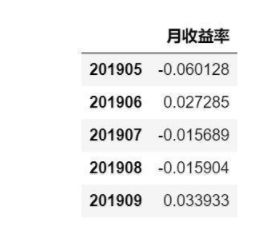
ret_monthly=y.groupby(y.index).sum()
ret_monthly.tail()
#将日收益率转化为年收益率
stock='601318'
df = ts.get_k_data(code=stock, ktype='D', autype='qfq', start='2007-3-1')
df.index=pd.to_datetime(df['date'])
logret=np.log(df.close/df.close.shift(1))[1:]
year=[]
d0=df.index
for i in range(0,np.size(logret)):
year.append(d0[i].strftime("%Y"))
y=pd.DataFrame(logret.values,year,columns=['年收益率'])
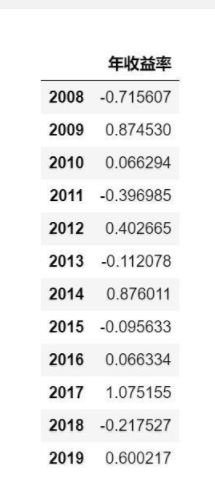
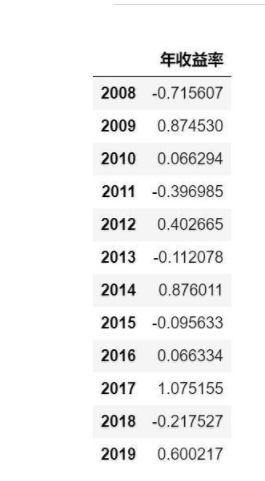
ret_annual=np.exp(y.groupby(y.index).sum())-1
ret_annual
计算股票的$\beta$系数和$\alpha值$
这里的beta和alpha系数都来自资本资产定价模型,先来看看CAPM:
E(ri)=rf+β(E(rm)−rf),
其中,E(ri)是股票i的预期收益率,rf是无风险利率,E(rm)是市场指数收益率;
β系数是系统性风险,在评估股市波动风险与投资机会的方法中,常用来衡量结构性与系统性风险,可以简单理解为个股波动相对大盘波动的偏离程度。CAPM的计量模型可以表示为:
ri=α+βrm+ε,
其中α可以理解为超额收益率,ε是随机扰动,可以理解为个体风险。
#先定义获取股票数据和计算收益率的函数
def get_return(code,startdate,endate):
df=ts.get_k_data(code,ktype='D',autype='qfq',
start=startdate,end=endate)
p1=np.array(df.close[1:])
p0=np.array(df.close[:-1])
logret = np.log(p1/p0)
rate=pd.DataFrame()
rate[code]=logret
rate.index=df['date'][1:]
return rate
#定义求beta和alpha的函数
def alpha_beta(code,startdate,endate):
mkt_ret=get_return('sh',startdate,endate)
stock_ret=get_return(code,startdate,endate)
df=pd.merge(mkt_ret,stock_ret,left_index=True,right_index=True)
x=df.iloc[:,0]
y=df.iloc[:,1]
beta,alpha,r_value,p_value,std_err=stats.linregress(x,y)
return (alpha,beta)
#定义求一系列股票在某个时间段的股票
def stocks_alpha_beta(stocks,startdate,endate):
df=pd.DataFrame()
alpha=[]
beta=[]
for code in stocks.values():
a,b=alpha_beta(code,startdate,endate)
alpha.append(float('%.4f'%a))
beta.append(float('%.2f'%b))
df['alpha']=alpha
df['beta']=beta
df.index=stocks.keys()
return df
startdate='2017-01-01'
endate='2018-11-09'
stocks={'中国平安':'601318','格力电器':'000651',
'招商银行':'600036','恒生电子':'600570',
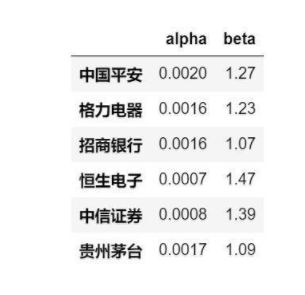
'中信证券':'600030','贵州茅台':'600519'}
stocks_alpha_beta(stocks,startdate,endate)
import statsmodels.api as sm
import tushare as ts
import pandas as pd
import numpy as np
def get_return(code,d0,d1):
df=ts.get_k_data(code,start=d0,end=d1)
p1=np.array(df.close[1:])
p0=np.array(df.close[:-1])
logret = np.log(p1/p0)
rate=pd.DataFrame()
rate[code]=logret
rate.index=df['date'][1:]
return rate
def beta(code,d0,d1):
s_ret=get_return(code,d0,d1)
sh_ret=get_return('sh',d0,d1)
df=pd.merge(s_ret,sh_ret,left_index=True,right_index=True)
y=df.iloc[:,0]
x=df.iloc[:,1]
x=sm.add_constant(x)
model=sm.OLS(y,x)
results=model.fit()
b=results.params[1]
return b
stocks={'中国平安':'601318','格力电器':'000651','招商银行':'600036',
'中信证券':'600030','贵州茅台':'600519'}
d0='2018-01-01'
d1='2018-11-13'
for stock in stocks.values():
s=list (stocks.keys())[list(stocks.values()).index(stock)]
print(s+"的市场风险beta:%.3f" % beta(stock,d0,d1))
中国平安的市场风险beta:1.278
格力电器的市场风险beta:1.219
招商银行的市场风险beta:1.053
中信证券的市场风险beta:1.425
贵州茅台的市场风险beta:1.145