一般图最大匹配-带花树算法
一般图最大匹配-带花树算法
前置知识:
二分图最大匹配
问题
对于一个图G(V,E),它的匹配M是二元组(u,v)组成的集合,其中u,v∈V,(u,v)∈E,并且M中不存在重复的点。
当|M|最大的时候,我们称M为G的最大匹配。
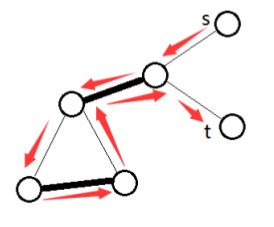
当G是一个二分图的时候,它的最大匹配可以用经典的匈牙利算法或网络流算法求解。然而当G是一个一般的图时,直接进行增广就变得不可行了,例如下面这个例子:
这个问题出现的原因,就是一个一般图中会含有奇环,即一个点数为2k+1,k>0的环,而如果经过一个奇环,那么会得到两条含有同一个点的匹配边,这其实是不符合定义的。那为什么二分图可以直接增广呢?因为二分图中不可能含有奇环,它所有的环都是偶环。因此,在一般图匹配问题中,我们需要一种改进算法来解决奇环的问题。
算法
基本算法依然是分为n个阶段寻找增广路。问题主要在奇环上,那么我们分析一下这个奇环的性质。首先,奇环中有2k+1个点,所以最多有k组匹配。这就是说,有一个点没有匹配,即这个点在环内两边的连边都不是匹配边,也只有这个点可以向环外连边。
发现了这个性质,我们可以把整个奇环缩成一个点。缩完点后的图如果可以找到一条增广路,那么原图中也可以找到一条增广路,因为如果增广路经过奇环那么奇环内的增广路可以还原出来。
这就是带花树算法的思想。整个求解过程分为n个阶段,每个阶段从没有匹配的s点开始bfs找增广路。搜索的开始,把s点加入队列中,标记它为A类点。如果从x点出发,搜索到了一个未标记的点,有两种情况。如果这个未标记点有匹配,那么把这个点设为B类点,它的匹配点设为A类点,加入队列继续增广。如果这个点没有匹配,又因为我们是从一个未匹配点开始进行搜索的,所以这说明我们找到了一条增广路,沿着过来的边找回去,展开带花树,修改搜索的过程中,如果我们遇到了偶环,那么不管它,因为它不会影响求解。如果遇到了一个奇环,那么我们找到当前点x和找到的点v,求出他们的最近公共花祖先,然后把环缩掉。这里我们用并查集实现。
我们在缩环的时候,处理出一个pre数组,表示我们回跳的时候走到这里该往哪一个方向走回去。回跳的时候,每次找到pre,然后修改这条边,接着跳到pre原来的match处。如果我们倒着进入一个花的时候,上方的边为非匹配边,那么我们会往下走,这个时候pre就应该往下设。中间相遇的位置pre互相连接,pre[x]=y,pre[y]=x。
算法分为n个阶段,每个阶段最多把整个图遍历一次,每个点会最多被缩n次花,所以总复杂度为O(n3)。
模板 —— 来自kuangbin
#include
vector<int>ans;
for(int i = 1;i <= m;i++)
{
u = p[i].first;
v = p[i].second;
memcpy(Graph,g,sizeof(g));
for(int j = 1;j <= N;j++)
Graph[j][u] = Graph[u][j] = Graph[j][v] = Graph[v][j] = false;
int cnt = getMatch();
//cout<
if(cnt < cnt0-1)
ans.push_back(i);
}
int sz = ans.size();
printf("%d\n",sz);
for(int i = 0;i < sz;i++)
{
printf("%d",ans[i]);
if(i < sz-1)printf(" ");
}
printf("\n");
}
return 0;
}