基础知识之针孔相机模型
针孔相机模型
文章目录
- 针孔相机模型
- Pinhole camera model
- The geometry and mathematics of the pinhole camera
- Rotated image and the virtual image plane
- Homogeneous coordinates
- 与实际数字图像坐标的关系
- 参考链接
翻译自Wikipedia,外加自己的一点理解。
原始文档:https://www.yuque.com/lart/idh721/zgv3i6
Pinhole camera model
针孔相机模型(Pinhole camera model),描述了三维空间中的点的坐标与其在理想针孔相机的图像平面上的投影之间的数学关系,其中相机光圈被描述为一个点,并且没有使用透镜来聚焦光线。**该模型不包括例如由镜头和有限尺寸的光圈引起的几何变形或未聚焦对象的模糊。也没有考虑到大多数实际的相机仅具有离散的图像坐标。**这意味着针孔相机模型只能用作从3D场景到2D图像的映射的一阶近似(a first order approximation)。其有效性取决于相机的质量,并且通常随着镜头失真效果的增加而从图像的中心到边缘降低。
针孔相机模型没有考虑到的一些影响可以得到补偿,例如通过对图像坐标应用适当的坐标变换;如果使用高质量的照相机,其他的影响就足够小以至于可以忽略不计。这意味着针孔相机模型通常可以用来合理地描述相机如何描绘三维场景,例如在计算机视觉和计算机图形学中。
The geometry and mathematics of the pinhole camera
这一部分主要基于下图来介绍针孔相机模型各参数之间的关系。这个图画的真心好,用来解释针孔相机模型非常方便直观。
这里的X1X2X3坐标系是左手系(我们一般绘制会画成右手系),这样的结果是,这里的OZ轴(也就是图中的OX3轴)实际上是与过去常见的右手系中的表示相反。
在图中示出了与针孔相机映射有关的几何形状。该图包含以下基本对象:
- 一个原点在O点的三维正交坐标系,这也是相机光圈(camera aperture)的位置。坐标系的三个轴被称为X1、X2、X3。X3轴指向相机的观察方向(viewing direction),称为光轴(optical axis)、主轴(principal axis)或主射线(principal ray)。由轴X1和X2张成的平面(the plane which is spanned by axes X1 and X2)是相机的正面,或称主平面(principal plane)。
- 一个像平面(image plane),其中三维世界通过相机光圈进行投影。像平面平行于轴X1和X2,并且在X3轴的负方向上与原点O距离为f,其中f是针孔相机的焦距(focal length)。针孔相机的实际实现意味着像平面的位置应使与X3轴在坐标-f处相交,其中f>0。
- 在光轴(optical axis)和像平面相交处的点R,该点称为主点(principal point)或图像中心(image center)。
- 真实世界中的某一点P,有相对于轴X1、X2、X3的坐标(x1,x2,x3)。
- 点P在相机中的投影线(projection line)。也就是图中穿过点P和点O的绿线。
- 点P在像平面上的投影,记作点Q。这个点由投影线(绿色)与像平面的交点表示。在任何实际情况下,我们可以假设x3>0,这意味着交点(intersection point)是定义良好的。
- 在像平面上也有一个二维坐标系:原点在R,轴Y1和Y2分别平行于X1和X2。点Q相对于这个坐标系的坐标是(y1,y2)。
假设摄像机的针孔孔径是无穷小的一点,所有的投影线都必须通过针孔孔径。在文献http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/FUSIELLO4/tutorial.html#x1-30003中,在三维空间中的这一点被称为光学(或镜头或相机)中心(optical or lens or camera center)。
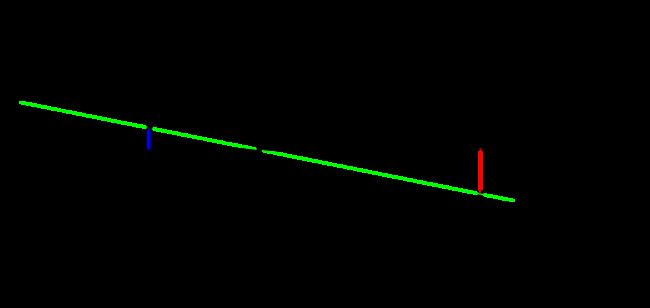
接下来,我们想了解坐标(y1,y2)上的点Q的与坐标(x1,x2,x3)上的点P之间的依赖关系。这可以在下图的帮助下完成,下图显示了与前一幅图相同的场景,但现在是沿着X2轴负方向从上方向下看。
在这个图中,我们看到两个相似的三角形,都有部分投影线(绿色)作为它们的斜边。左面的三角的两条直角边长度为-y1和f,右三角的为x1和x3。因此可以使用tan关系写成形式 − y 1 f = x 1 x 3 \frac{-y_1}{f}=\frac{x_1}{x_3} f−y1=x3x1或 y 1 = − f x 1 x 3 y_1=-\frac{fx_1}{x_3} y1=−x3fx1的形式。相似的,沿着X1轴的负方向观察,可以得到: − y 2 f = x 2 x 3 \frac{-y_2}{f}=\frac{x_2}{x_3} f−y2=x3x2或者 y 2 = − f x 2 x 3 y_2=-\frac{fx_2}{x_3} y2=−x3fx2。这可以整体写成如下形式:
该表达式描述了点P的三维坐标(x1,x2,x3)与其在像平面上的投影点Q的图像坐标(y1,y2)之间的关系。
Rotated image and the virtual image plane
针孔摄像机描述的从3D坐标到2D坐标的映射是透视投影(perspective projection),然后在图像平面中旋转180°。这对应于真实的针孔摄像机的工作方式;产生的图像旋转了180°,并且投影对象的相对大小取决于它们到焦点的距离,而图像的整体大小取决于像平面和焦点之间的距离f。为了产生不旋转的图像(这是我们对相机的期望),有两种可能性:
- 将像平面中的坐标系旋转180°(沿Y1或Y2任一方向)。这是任何针孔相机的实际实现方式解决该问题的方式。对于照相相机(photographic camera),我们在观看之前先旋转图像;对于数码相机(digital camera),我们按旋转的顺序读出像素。
- 将像平面放置在X3轴的f处而不是-f处,然后重新进行以前的计算。这将生成虚(或正面)像平面(virtual (or front) image plane),该像平面在实践中无法实现,但提供的理论相机比实际相机更易于分析。
在这两种情况下,从3D坐标到2D图像坐标的结果映射由上面的表达式给出,但是不再有负号。因此可得:

Homogeneous coordinates
从空间中点的3D坐标到2D图像坐标的映射也可以用齐次坐标(homogeneous coordinates)表示。假设x是齐次坐标(4维向量)中3D点的表示,而y则是该点在针孔相机(3维矢量)模型下,在图像中的表示。那么以下关系成立
![]()
其中C是3×4的相机矩阵(camera matrix),而 ∼ \sim ∼表示投影空间(projective spaces)元素之间的等价性(我们不考虑原始的相等,而是考虑按非零倍数伸缩后的相等)。这意味着左侧和右侧最多相差一个非零的标量倍数。这种关系的结果是C也可以看作是投影空间的元素。如果两个相机矩阵等价于标量乘法(仅相差个标量倍数),则它们是等效的。
针孔相机映射的这种描述(作为线性变换C,而不是作为两个线性表达式的一部分),可以简化3D和2D坐标之间关系的许多推导。
在计算机视觉中,相机矩阵或(相机)投影矩阵(camera matrix or (camera) projection matrix) 是描述针孔相机从真实世界3D点到图像上2D点的映射的3×4矩阵。
由针孔相机模型关系:
用齐次坐标(homogeneous coordinates)改写,进一步扩展和简化,这里不考虑原始对应的相等,而是考虑按非零倍数伸缩后的相等:
最终得到:
即:
这里的C可以进一步改写:
最后一步是C本身是一个投影元素。
更多细节参考对应的wiki。
与实际数字图像坐标的关系
这个时候,像平面的坐标实际上是从左上角开始的,所以这里对应的主点需要计算出来,相较于原始的实现:
这里需要修改这里的y1和y2。假设对应的主点的坐标为(c1,c2),则调整后可以得到:
( y 1 − c 1 ) × x 3 / f = x 1 ( y 2 − c 2 ) × x 3 / f = x 2 (y_1-c_1) \times x_3 / f = x_1 \\ (y_2-c_2) \times x_3 / f = x_2 (y1−c1)×x3/f=x1(y2−c2)×x3/f=x2
这里的正负号已经隐含在了计算中。
参考链接
- 针孔相机模型:https://en.wikipedia.org/wiki/Pinhole_camera_model
- 相机矩阵:https://en.wikipedia.org/wiki/Camera_matrix