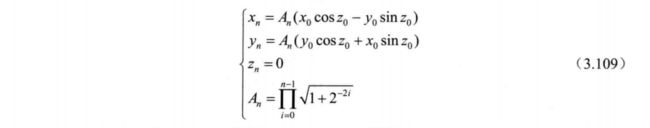CORDIC算法详解(一)-CORDIC 算法之圆周系统之旋转模式
CORDIC算法详解(一)- CORDIC 算法之圆周系统之旋转模式( Rotation Mode )
文章目录
- CORDIC算法详解(一)- CORDIC 算法之圆周系统之旋转模式( Rotation Mode )
- 1 CORDIC 算法之圆周系统及其数学应用
- 1.1 圆周系统之旋转模式( Rotation Mode )
- 1.2 思考
- 1.3 CORDIC算法应用
- 1.3.1 目标旋转角度的正、 余弦函数值
- 1.3.1 极坐标系向直角坐标系的转换
- 1.4 举例
- CORDIC 算法之圆周系统及其数学应用结束
网上有很多类似的介绍,但是本文会结合实例进行介绍,尽量以最简单的语言进行解析。
CORDIC ( Coordinate Rotation Digital Computer ) 是坐标旋转数字计算机算法的简称,
由 Vloder• 于 1959 年在设计美国航空导航控制系统的过程中首先提出[1], 主要用于解决导航系统中三角函数、 反三角函数和开方等运算的实时计算问题。 1971 年, Walther 将圆周系统、 线性系统和双曲系统统一到一个 CORDIC 迭代方程里 , 从而提出了一种统一的CORDIC 算法形式[2]。
CORDIC 算法应用广泛, 如离散傅里叶变换 、 离散余弦变换、 离散 Hartley 变换、Chirp-Z 变换、 各种滤波以及矩阵的奇异值分解中都可应用 CORDIC 算法。 从广义上讲,CORDIC 算法提供了一种数学计算的逼近方法。 由于它最终可分解为一系列的加减和移位操作, 故非常适合硬件实现。 例如, 在工程领域可采用 CORDIC 算法实现直接数字频率合成器。 本节在阐述 CORDIC 算法三种旋转模式的基础上, 介绍了利用 CORDIC 算法计算三角函数、 反三角函数和复数求模等相关理论。 以此为依据, 阐述了基于 FPGA 的 CORDIC 算法的设计与实现及其工程应用。
整个系列分别从圆周系统、 线性系统和双曲系统及硬件实现进行分析,如下:
CORDIC算法详解(一)- CORDIC 算法之圆周系统之旋转模式( Rotation Mode )
CORDIC算法详解(二)- CORDIC 算法之圆周系统之向量模式(Vectoring Mode)
CORDIC算法详解(三)- CORDIC 算法之线性系统及其数学应用
CORDIC算法详解(四)- CORDIC 算法之双曲系统及其数学应用
CORDIC算法详解(五)- 统一的 CORDIC 算法形式
CORDIC算法详解(六)- CORDIC 算法的硬件实现
其中第五篇及第六篇后会放出相关参考资料及源码。
1 CORDIC 算法之圆周系统及其数学应用
在圆周系统下, CORDIC 算法解决了三角函数的计算问题,其中圆周系统又分旋转模式和向量模式。
1.1 圆周系统之旋转模式( Rotation Mode )
如图 3.69 所示, 在单位圆上, 向量 OP与X轴正半轴夹角为 α , 故P点坐标可表示为式(3.91):
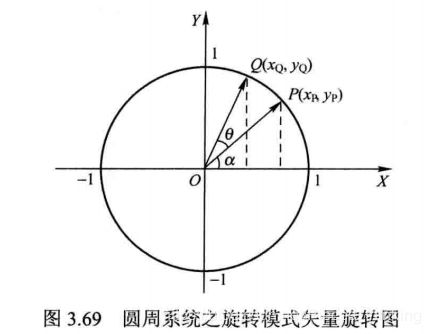

将向量 OP 逆 时 针 旋 转θ角 至 向 量 OQ,此 时 OQ与X轴正半轴夹角为 α + θ ,故 Q 点坐标可以表示为:

这里定义 θ为目标旋转角度。 根据三角函数公式可将式 (3.92) 展开为:

将式 (3.91 ) 代入式 (3.93) 可得:
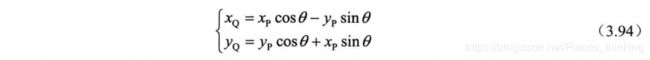
提取 cosθ , 式 (3.94) 可重新表示为:
![]()
从式 (3.95 ) 中可看出, cosθ只是改变了目标向量OQ的模长。 如果去掉 cosθ , 如图 3.70所示, 此时 OP旋转θ角之后到达 OR, 这种旋转称之为伪旋转( Pseudo Rotation) 。不难看出, OQ与OR 幅度 上 的 差 异, 且 可 证 明 向 量 OP 与 PR是正交的。 此时R点坐标可表示为:
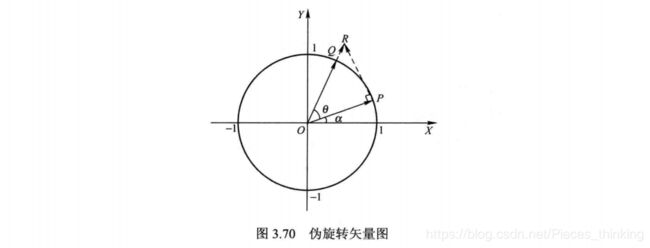

至此, 可通过对伪旋转的输出加以补偿来获得真实旋转的结果。
PS:对比可知每次旋转的角度是正确的,但是模值增大了1/cosθ
注意:并不能通过数学方法去除cosθ,但是去除cosθ可以简化坐标平面旋转的计算操作。
对于伪旋转, 可将 θ分解为一系列的微小角度的和, 即:
![]()
这样, 将一次旋转分解成为一系列的微旋转。 由式 (3.96) 可知, 第i+1 次旋转后的结果为:

下一步至关重要, 正是它使得该算法非常易于硬件实现, 即令:
![]()
这里di∈{-1,1}, 结合式( 3.99), 式 (3.98) 可重新改写为:
![]()
由式(3.100), 不难看出, 每次微旋转只需要加法 、 减法和移位操作即可完成。为了确定di的值,引入一个新的变量z,定义为:
![]()
z 初 始 化 为θ,即z0=θ,根据条件,对zi执行加或者减tan-12-i操作,使得z的最终值为0 ,该条件由di决定,即:

di为+1时表示逆时针旋转,为-1时表示顺时针旋转 。z的迭代过程是将z收敛于零的过程,也正是将θ分解为一系列θi的过程, 故zi可认为是第i次旋转剩余的角度。至此 ,CORDIC 算法之圆周系统的旋转模式迭代过程可表示为:

1.2 思考
- (1 ) 由式 (3.99) 所确定的目标旋转角度的范围;
![]()
- (2) 如何确定伪旋转到真实旋转的模长补偿因子。
(1)根据式 (3.99 ) 可确定一系列θi的值, 如表 3.17 所示, 还可确定目标旋转角度θ的最大值 θmax 和 最 小 值 θmin , 如式( 3.104 ) 所示。
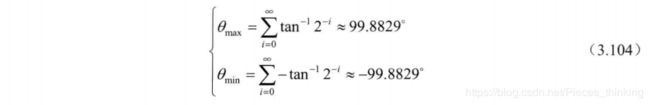
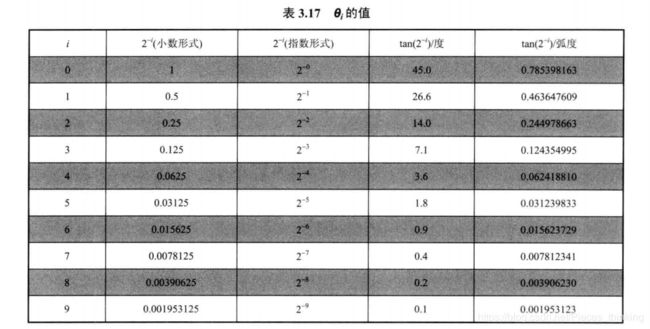
以目标旋转角度 55° 为例, 它可分解为
55° = 45.0° + 26.6° -14.0°- 7.1° + 3.6° + 1.8° - 0.9°
其迭代过程中角度的变化状况如表 3.18 所示。 假设初始向量位于X轴 正 半 轴, 前 3 次 的 微旋转如图 3.71 所示。


(2)在很多场合中需要目标旋转角度可以覆盖[-180°,180°], 这就需要预处理。 预处理的机制如表 3.19 所示, 不难看出, 只有当目标旋转角度|θ|>π/2 时需要预旋转 π/2 , 用公式表示如式 (3.105) 所示。


据此, 旋转过程可如图 3.72 所示。

由图 3.71 可以看出, 每次微旋转都导致向量模长发生了变化。以Ki表示第 i次微旋转模长补偿因子, 故第 i次微旋转真实旋转的结果应为:

其中,由于在伪旋转中,去掉了cosθi,所以Ki=cosθi 由式 (3.99) 可知:
![]()
![]()
若总的旋转次数为n, 则总的模长补偿因子K可表示为:

当n趋于无穷大时,K 逼近 0.607252935。
这部分计算,可以由matlab进行迭代计算:
具体如下:
close all;
clear;
clc;
% 初始化
die = 16;%迭代次数
jiao = zeros(die,1);%每次旋转的角度
cos_value = zeros(die,1);%每次旋转的角度的余弦值
K = zeros(die,1);%余弦值的N元乘积
K_1 = zeros(die,1);%余弦值的N元乘积的倒数
for i = 1 : die
a = 2^(-(i-1));
jiao(i) = atan(a);
cos_value(i) = cos(jiao(i));
if( i == 1)
K(i) = cos_value(i);
K_1(i) = 1/K(i);
else
K(i) = K(i-1)*cos_value(i);
K_1(i) = 1/K(i);
end
end
jiao = vpa(rad2deg(jiao)*256,10)
cos_value = vpa(cos_value,10)
K = vpa(K,10)
K_1 = vpa(K_1,10)

从上表也可以看出,当迭代次数为16,i=15时,cosθi的值已经非常趋近于1了,∏cosθi的值则约等于0.607253,1/∏cosθi为1.64676。所以当迭代次数等于16时,通过迭代得到的点坐标已经非常接近之前假设中的点坐标。
1.3 CORDIC算法应用
1.3.1 目标旋转角度的正、 余弦函数值
式中, 当 n 趋于无穷大时, An逼近 1.646760258。 根据式 (3.109 ) 可知, 令 x0=1/An且y0 = 0 可得目标旋转角度的正、 余弦函数值, 如图 3.73 所示。 此时, 初始化 z0 即为目标旋转角度 。 需要注意的是当目标旋转角度|θ|>π/2 时应先预处理 。

1.3.1 极坐标系向直角坐标系的转换
同样地, 由式 ( 3.109 ) 出发, 令 x0=r且y0 = 0,z0 =θ,则可以实现极坐标系向直角坐标系的转换, 如图 3.75 所示。 显然, 这里x0代表了极径, z0 代表了极角。

1.4 举例
利用CORDIC算法,计算cosθ和sinθ,其中θ=π/4(迭代次数16)
- x0=1/An=1/1.646760258=0.607253;
- y0 = 0;
- z0=π/4(由于|θ|<π/2,所以不需要进行预处理);
- 经过16次迭代计算后,得到的x16 和y16分别为cosθ和sinθ。
相关程序如下:
close all;
clear;
clc;
% 初始化
die = 16;%迭代次数
x = zeros(die+1,1);
y = zeros(die+1,1);
z = zeros(die+1,1);
x(1) = 0.607253;%初始设置
z(1) = pi/4;%待求角度θ
%迭代操作
for i = 1:die
if z(i) >= 0
d = 1;
else
d = -1;
end
x(i+1) = x(i) - d*y(i)*(2^(-(i-1)));
y(i+1) = y(i) + d*x(i)*(2^(-(i-1)));
z(i+1) = z(i) - d*atan(2^(-(i-1)));
end
cosa = vpa(x(17),10)
sina = vpa(y(17),10)
c = vpa(z(17),10)
最后得到的结果:
- x16=0.707095876358217
- y16=0.707117836980767
证明算法思路正确。