平面最近点对问题求解
平面最近点对问题求解
问题描述:
最近点对问题是指求解平面点集n个点中距离最近的两个点间的问题。为简单起见,在二维坐标平面来考虑该问题。如果说讨论的点以标准二维坐标给出,则有点
和
,那么这两点之间的距离
。通过这个公式,我们可以计算平面上任意两点之间的距离。
本章主要通过两种方法来求解
- 蛮力法
- 分治法
1.蛮力法
顾名思义,蛮力法指的就是通过遍历所有解之后通过对比求出最近点对问题。
基本思路:
对平面中的n个点两两进行组队,计算并记录最小距离。这里需要注意两个问题,其一,点对之间的距离是没有方向性的,即dis( Pi , Pj )=dis,( Pj , Pi ),所以任意两点只需要计算一次即可。其二,计算的时候如果只是求解大小,可以不同开方,这样有一定的优化,简化了公式的计算。
这里以杭电ACM 1007作为例子,蛮力法代码如下:
(由于是蛮力法,所以时间复杂度很高,无法AC1007,这里只是作为例子讲解)
题目链接:杭电ACM 1007
#include "stdio.h"
#include "math.h"
double Point[100001][2];
int main()
{
int N,a=0,b=0,i,j;
double Min;
while(scanf_s("%d",&N) && N!=0)
{
Min=9999999;
for(i=0;i"%lf%lf",&Point[i][0],&Point[i][1]);
for(i=0;i1;i++) //N-1
{
for(j=i+1;j//这里可以避免对同一对坐标计算两次距离
{
double dis=(Point[j][1]-Point[i][1])*(Point[j][1]-Point[i][1])+
(Point[j][0]-Point[i][0])*(Point[j][0]-Point[i][0]);
if(disdouble dis=sqrt((Point[b][1]-Point[a][1])*(Point[b][1]-Point[a][1])+
(Point[b][0]-Point[a][0])*(Point[b][0]-Point[a][0]));
printf("%.2lf\n",dis/2);
}
return 0;
}
2.分治法
分治法思路:
1) 把它分成两个或多个更小的问题;
2) 分别解决每个小问题;
3) 把各小问题的解答组合起来,即可得到原问题的解答。小问题通常与原问题相似,可以递归地使用分而治之策略来解决。
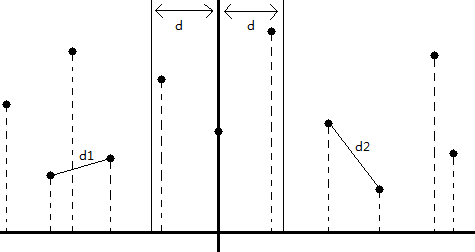
这里的分治算法的主要思路是将平面上的n个点分为两个子集S1,S2。每个子集中有n/2个点,然后递归的在每个子集中求解最近点对,两边求得的结果如图所示:
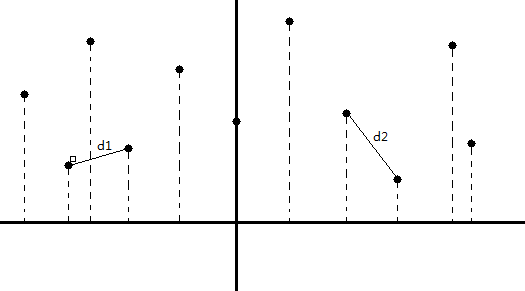
那么可以看出左边的最近点对的距离为d1,右边为d2.但是最近对可能一个点在S1中而另一个点在S2中。这样,我们,就要去想办法对其进行合并,然后求得合并区域的最近对距离,假设为d3,那么只需要比较d1,d2,d3的大小关系即可,最小的就是平面最近对的距离。通过分析我们可以知道,如果存在这样的最近对的点,那么这个点在S1集合中,肯定是横坐标最靠近中位线 L 的点,S2中同理。那么这个范围如何划定呢?
设d=min(d1,d2)假定中位线横坐标为X,那么范围就是[X-d,X+d].这个范围是怎么划定的呢?根据平面中点的位置我们就可以知道,两点的距离为横纵坐标之间的差值的平方和。那么如果要存在这样的点,他们之间的横坐标之间的差值的绝对值必须要小于等于d(这里包括这点恰好就在中位线 L 上)。这样可以筛选出横坐标为[X-d,X+d]的区域。如下图所示:
可以看出这个区域中包含三个点,只需要求出这三个点之间的最近点对即可(蛮力法)。这里还需要注意一点,上面是通过横坐标筛选的这个区域,这里可以根据纵坐标将纵坐标差的绝对值大于 d 的坐标剔除。
这里是分治法求解代码:
#include "stdio.h"
#include "math.h"
#include
#include "algorithm"
#define MAX 100005
const double inf = 1e20;
struct Point{
double x;
double y;
};
Point p[MAX];
int ans[MAX];
double dis(Point p1,Point p2)
{
return sqrt((p2.y-p1.y)*(p2.y-p1.y)+(p2.x-p1.x)*(p2.x-p1.x));
}
bool cmpy(const int & a,int& b)
{
return p[a].y < p[b].y;
}
bool compxy(const Point& p1,Point& p2)
{
if(p1.x!=p2.x)
return p1.xreturn p1.ydouble min(double a,double b)
{
return adouble divide(int left,int right)
{
double d=inf;
/*这里指只有一个点,那么最近点对的话距离自然就是inf了*/
if(left==right)
return d;
//这里是判断是否为只有两个点,如果只有两个点的话那么直接求解。
if(left+1==right)
return dis(p[left],p[right]);
//右移除2,对区域进行合理的划分,使得左右两边保持大致相等个数点
int mid=(left+right)>>1;
double d1=devide(left,mid);
double d2=devide(mid+1,right);
d=min(d1,d2);
int i,j,k=0;
//通过横坐标确定[X-d,X+d]区域
for(i=left;i<=right;i++)
{
if(fabs(p[mid].x-p[i].x)<=d)
ans[k++]=i;
}
//通过排序,确定这写点按照纵坐标升序
std::sort(ans, ans + k, cmpy);//线性扫描
for(i=0;i1;i++)
{
for(j=i+1;jdouble distance=dis(p[ans[i]],p[ans[j]]);
if(distance return d;
}
int main()
{
int i,j,N;
while(scanf_s("%d",&N) && N!=0)
{
for(i=0;i"%lf%lf",&p[i].x,&p[i].y);
std::sort(p,p+N,compxy);//这里按照横坐标大小预排序,利用横坐标求中位线
printf("%.2lf\n",divide(0,N-1)/2);
}
return 0;
}
其实,分治法的理解确实比较难,我在看了算法导论上面讲解之后也是一头雾水。所以后面就百度最近点对的分治算法。看了好多博客,最后终于明白了。所以这里真的非常感谢那些在自己明白了算法之后还乐于分享理解思路的博主们!所以,这里我也写一下自己对于算法的大概理解吧,或许在冥冥之中会给你带来一点点头绪。
Up_Junior1.
- *. ↩