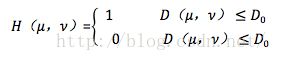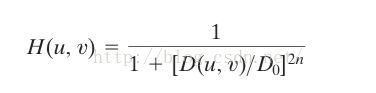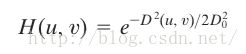关于数字图像处理中不同的低通滤波器的区别以及cut-off frequency 对于图像的影响

最近做课设的时候遇到了低通滤波器的问题。翻阅了下书籍，得到了一些收获，想来分享下。如有不对的地方，请大神斧正。

首先要清楚的概念是，图像（假设是灰度图，便于描述，或者是单个channel的图）在时域和频域中的分别是什么含义。在时域中，很显然，对应的是每个像素，每个像素上的点的灰度值。 如果该图像用matlab显示的话，（x,y）代表图中的每个像素，每个像素对应Z的值就是该图像在这个像素点的灰度。那么在频域中，也就是如果我对这个矩阵进行傅里叶变换，我们得到的该图像在频域中的表达。 图像在频域中，是该图像的颜色变化的剧烈程度。低频部分表示那些颜色变化不是很剧烈的部分，而高频部分则是那些颜色变化剧烈的部分。举个例子，如果我们有一副海洋和沙滩的图，沙滩上可能有些人以及其他的东西。 那么，我们可以发现，图像中，低频部分所关联的就是颜色变化平滑的，或者说不太变化的，如大片的沙滩以及海洋。而高频部分则关联的是颜色变化剧烈的部分，如海洋和沙滩交接的部分，或者其他颜色变化剧烈的东西，一般高频部分所关联的是两个颜色的相交接的部分，而这一般都发生在两个不同物体的轮廓上，所以，如果我们只取特定高频的部分，那我们就能得到物体的轮廓了（本文主要讲解低通滤波器，所以涉及的基本都是低频部分，高频部分会在其他博文中阐述）。

好了，现在我们对于图像的傅里叶变化有了一个大概的认识。那么我们来说说为什么在图像处理时，要使用低通滤波器呢。出于某些目的，我们希望我们的图像不那么清晰，即去除噪点或者不要有那么多的细节（比如，美图秀秀中磨皮。。。 我们不希望皮肤上的毛孔都出现在图像上，但现在的手机像素都很高，所以如果不做处理，那么脸上就会有很多细节都展现在图片上，如痘印啊，粗大的毛孔等）。那么这个时候，我们就需要使用低通滤波器了，即把那些高频的细节都过滤掉，留下的就只有平滑的皮肤了。

接下来，在来看看低通滤波器的种类。低通滤波器的种类有很多，比较常接触的大概是以下几类：

（1）理想的低通滤波器

   以上是二维中，低通滤波器的公式。其实很好理解，一维中的低通滤波器就是一个窗口函数，在D0的时候，直接从1变成0. 那么二维中的低通滤波器就是讲一维中的低通滤波器绕着y轴旋转一周，所得到的圆柱就是二维中低通滤波器的样子。而绕的点一般是图像的中心（P,Q代表了图像的横纵像素点的个数）。而D0 代表了截止频率。matlab中自己构造理想低通滤波器的话，代码应该如下所示：

lowPF = zeros(p,Q);

for i = 1:P
    for j =1:Q
        if((i-P/2)^2+(j-Q/2)^2 <=D0^2)
            lowPF(i,j) = 1;
        end
            
    end
end

figure;
title('low_pass_filter_cf=D0');
imshow(lowPF,[]);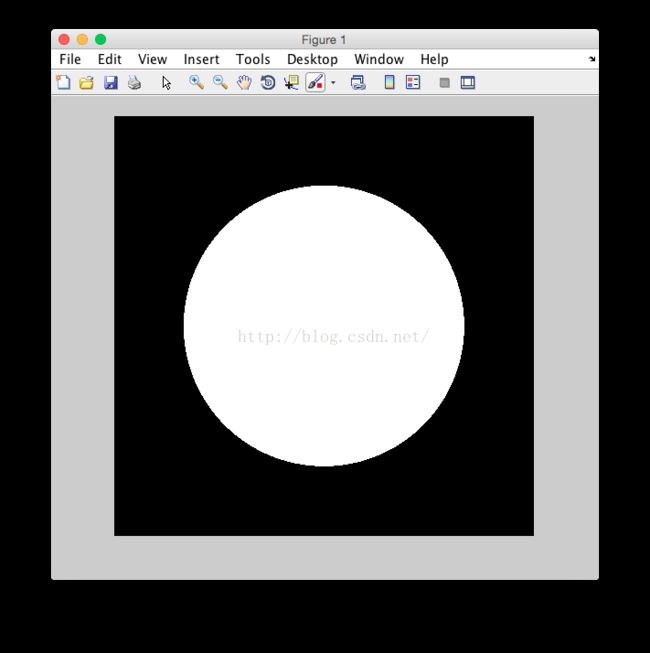

而得到的图像应该是这样的：

由于理想滤波器的傅里叶反变换的是二维的sinc函数，即将一维的sinc函数绕着y轴旋转一周（就像水波浪漾开那样），所以当用这种滤波器处理图像时，在边缘变化剧烈的地方会产生ringing。

然而正如它的名字一样，它是理想低通滤波器，在实际使用中，我们不会使用这种滤波器，原因有二：首先是在实际上来说，不可能产生瞬时的阶跃，即在D0位置，我们不可能能马上从1跳到0.二是因为理想滤波器所得到的图片ringing现象很严重（后文会有详细说明）

（2）Butterworth 低通滤波器

以上是Butterworth滤波器的公式，相比于理想滤波器，它的阶跃部分更加圆滑，而幂系数n可以改变滤波器的形状，n越大，则该滤波器越接近于理想滤波器。以下为该滤波器的侧面图，以及用图像显示的图。

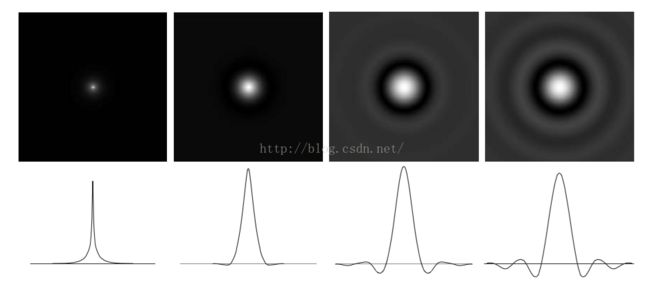
上图为n取1-4所得到的butterworth函数傅里叶反变换所得到的函数的侧视图，我们可以看到n越小，晕越少。

与理想滤波器相比，Butterworth函数的傅里叶反变换所产生的晕比理想滤波器更平滑，所以该滤波器形成的图片的ringing更少，且容易实现。以下是该滤波器的matlab代码

lowPF = zeros(P,Q);
n=1;

for i = 1:P
    for j =1:Q
      
            lowPF(i,j) = 1/(1+((i-P/2)^2+(j-Q/2)^2)^0.5/D0)^(2*n);
  
            
    end
end

figure;

imshow(lowPF,[]);

（3）.高斯低通滤波器

以上为高斯低通滤波器的公式，我们可以看到因为高斯滤波器是e的幂函数，所以该滤波器的傅里叶反变换应该也是e的幂函数，所以不会有晕的现象，相比以上两种滤波器，ringing现象几乎没有。以下为高斯滤波器的侧视图以及图像显示的图

高斯滤波器的matlab代码

lowPF3 = zeros(P,Q);

for i = 1:P
    for j =1:Q
        lowPF3(i,j) = exp(-((i-P/2)^2+(j-Q/2)^2)/(2*D0^2));
            
    end
end

（4）滤波器截止频率对于图像的影响

就像我们前面所说的，高频的部分是图像的细节，那么如果截止频率越大，则保留的细节越多，相反截止频率越小，那么就会有更多的细节被过滤了，所以图像会更模糊，且ringing现象会更明显。

以下上图分别为截止频率为460、160、60、30得到的图

可以发现当截止频率变为160时，字母a周围的晕变得十分明显，当截止频率变为30时，图像整个变得十分模糊。

(5)相同截止频率下选择不同滤波器的效果

以上我们可以看到相同的截止频率下，理想滤波器的ringing效果十分明显，Butterworth的有点朦胧，但是ringing效果比较弱，而高斯滤波器效果很不错。