题目:
给定无向连通图中一个节点的引用,返回该图的深拷贝(克隆)。图中的每个节点都包含它的值 val(Int) 和其邻居的列表(list[Node])。
Given a reference of a node in a connected undirected graph, return a deep copy (clone) of the graph. Each node in the graph contains a val (int) and a list (List[Node]) of its neighbors.
示例:
输入:
{"$id":"1","neighbors":[{"$id":"2","neighbors":[{"$ref":"1"},{"$id":"3","neighbors":[{"$ref":"2"},{"$id":"4","neighbors":[{"$ref":"3"},{"$ref":"1"}],"val":4}],"val":3}],"val":2},{"$ref":"4"}],"val":1}
解释:
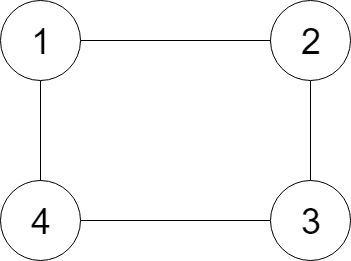
节点 1 的值是 1,它有两个邻居:节点 2 和 4 。
节点 2 的值是 2,它有两个邻居:节点 1 和 3 。
节点 3 的值是 3,它有两个邻居:节点 2 和 4 。
节点 4 的值是 4,它有两个邻居:节点 1 和 3 。
提示:
- 节点数介于 1 到 100 之间。
- 无向图是一个简单图,这意味着图中没有重复的边,也没有自环。
- 由于图是无向的,如果节点 p 是节点 q 的邻居,那么节点 q 也必须是节点 p 的邻居。
- 必须将给定节点的拷贝作为对克隆图的引用返回。
Note:
- The number of nodes will be between 1 and 100.
- The undirected graph is a simple graph, which means no repeated edges and no self-loops in the graph.
- Since the graph is undirected, if node p has node q as neighbor, then node q must have node p as neighbor too.
- You must return the copy of the given node as a reference to the cloned graph.
解题思路:
涉及到图的遍历无非就是DFS(深度优先搜索)、BFS(广度优先搜索),可以先看前几日的这篇文章:
BFS就需要借助队列实现,DFS可以借助栈也可以直接用递归实现。就这道题而言直接用递归更好一些,无需开辟额外的数据结构空间记录节点。BFS、DFS写法相对固定,建议花点时间一次性理解透,一劳永逸。
这道题思路很清晰,关键点是如何深拷贝随机节点,可以参考链表的这篇文章:LeetCode 138:复制带随机指针的链表 Copy List with Random Pointer
链表是线性的,可以 复制节点到每个节点之后,很巧妙的完成深拷贝。显然图这样的树状结构无法用这种方法,只能借助数据结构记录已拷贝过的节点。这种需要映射新旧节点关系自然就是用散列表(字典)。
Java:
class Solution {
public Node cloneGraph(Node node) {
if (node == null) return node;
Queue queue = new LinkedList<>();//借助队列实现BFS
Map map = new HashMap<>();//哈希映射
Node head = new Node(node.val, new ArrayList<>());//头节点
map.put(node, head);//哈希映射原节点和新节点
queue.add(node);//原节点加入到队列
while (!queue.isEmpty()) {//队列不为空就重复循环
Node tmp = queue.poll();//弹出队列头节点
for (Node n : tmp.neighbors) {//遍历邻居节点
if (!map.containsKey(n)) {//字典的键不包含该节点时
map.put(n, new Node(n.val, new ArrayList<>()));//新建映射关系加入字典
queue.add(n);//加入队列
}
map.get(tmp).neighbors.add(map.get(n));//加入邻居节点
}
}
return head;
}
}
Python3:
class Solution:
def cloneGraph(self, node: 'Node') -> 'Node':
if not node: return node
head = Node(node.val, [])#头节点
map = {node: head}#初始化字典,并建立新旧节点的映射关系
queue = collections.deque()#队列
queue.append(node)#原节点加入队列
while queue:#队列不为空
tmp = queue.popleft()#弹出队列头节点
for n in tmp.neighbors:#遍历邻居节点
if n in map.keys():#n节点存在于字典的键里时
map[tmp].neighbors.append(map[n])#直接加入到新节点的邻居节点
else:
map[n] = Node(n.val, [])#新建节点并建立映射关系
map[tmp].neighbors.append(map[n])#由新建的映射关系取出节点并加入邻居节点
queue.append(n)#该邻居节点加入队列
return head
DFS:
递归完成的深度优先搜索非常简洁,比较容易理解,唯一要注意的就是需要把字典定义在函数外。
Java:
class Solution {
Map map = new HashMap();
public Node cloneGraph(Node node) {
if (node == null) return node;
map.put(node, new Node(node.val, new ArrayList<>()));//每次都要新建节点并建立映射关系
for (Node n : node.neighbors) {
if (map.containsKey(n)) map.get(node).neighbors.add(map.get(n));
else map.get(node).neighbors.add(cloneGraph(n));
}
return map.get(node);
}
}
Python3:
class Solution:
map = dict()
def cloneGraph(self, node: 'Node') -> 'Node':
if not node: return node
self.map[node] = Node(node.val, [])
for n in node.neighbors:
if n in self.map.keys():
self.map[node].neighbors.append(self.map[n])
else:
self.map[node].neighbors.append(self.cloneGraph(n))
return self.map[node]
注意:
python中的字典取values时可以 dict().get(key) 也可以 dict[key] 时间复杂度都为1,但是在做算法题时肯定要用 dict[key] 这种方式。因为 get() 方法虽然效果一样,但是反复调用函数造成的时间消耗非常高,python语言本来就慢,应该养成尽可能优化代码的习惯。
欢迎关注微.信公.众号:爱写Bug