基于GBDT的商品销售预测

背景

商品销售预测几乎时每个运营部门的必备数据支持项目，无论是大型促销活动还是单品营销都是如此。这个项目就是针对某单品做的订单量预测。

项目主要应用技术

本项目用到的主要技术包括：

• 基本预处理，包括缺失值填充。
• 数据建模，包括交叉验证、集合回归方法GradientBoostingRegressor。
• 图形展示，使用matplotlib做折线图展示。

主要用到的库包括：pandas、numpy、matplotlib、sklearn、pickle，其中sklearn是数据建模的核心库。

本项目技术重点是设置集成回归算法的不同参数值，通过交叉验证寻找每个参数值的效果，并寻找最优值，得到最优值下的集成回归算法模型。这种参数优化方法需要手动调整选择参数，这种方法的好处在于，可以观察到每个参数的变化趋势。

1、导入库

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import pickle
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import accuracy_score
from sklearn.metrics import mean_squared_error as mse
from sklearn.ensemble import GradientBoostingRegressor

2、读取数据

df = pd.read_table("products_sales.txt", sep=',')

3、数据审查

df.shape

(731, 11)

df.head()

	limit_infor	campaign_type	campaign_level	product_level	resource_amount	email_rate	price	discount_rate	hour_resouces	campaign_fee	orders
0	0	6	0	1	1	0.08	140.0	0.83	93	888	1981
1	0	0	0	1	1	0.10	144.0	0.75	150	836	986
2	0	1	1	1	1	0.12	149.0	0.84	86	1330	1416
3	0	3	1	2	1	0.12	141.0	0.82	95	2273	2368
4	0	0	0	1	1	0.10	146.0	0.59	73	1456	1529

• limit_infor 是否有限购字样信息提示
• campaign_type 促销活动类型
• campaign_level 促销活动重要性
• product_level 商品重要性分级
• resource_amount 促销资源位数量
• email_rate 发送电子邮件中包含该商品的比例
• price 单品价格
• discount_rate 折扣率
• hour_resouces 在促销活动中展示的小时数
• campaign_fee 商品的促销费用
• orders 单品在活动中形成的订单量，是目标变量

df.info()

RangeIndex: 731 entries, 0 to 730
Data columns (total 11 columns):
 #   Column           Non-Null Count  Dtype  
---  ------           --------------  -----  
 0   limit_infor      731 non-null    int64  
 1   campaign_type    731 non-null    int64  
 2   campaign_level   731 non-null    int64  
 3   product_level    731 non-null    int64  
 4   resource_amount  731 non-null    int64  
 5   email_rate       731 non-null    float64
 6   price            729 non-null    float64
 7   discount_rate    731 non-null    float64
 8   hour_resouces    731 non-null    int64  
 9   campaign_fee     731 non-null    int64  
 10  orders           731 non-null    int64  
dtypes: float64(3), int64(8)
memory usage: 62.9 KB

从结果可以看到，price列包含缺失值，缺失了2条。

到这里数据审查就结束了。对于回归来说，涉及的数据审查还有：数据异常值查看、数据量纲差异、特征相关性等。在这个项目中我们要用的梯度提升树是一种基于CART（分类回归树）的集成算法，对上面这些问题能有效应对，因此没有做更多的审查。

4、数据预处理

根据步骤3得到的结论，需要对price中的缺失值进行处理。考虑到整个样本量比较少，因此做填充处理；而price列是数值型，选择填充为均值。

# 缺失值填充
fill_df = df.fillna(df['price'].mean())

# 分割数据集X和y
X = fill_df.iloc[:, :-1]
y = fill_df.iloc[:, -1]

# 分割训练集和测试集
Xtrain, Xtest, ytrain, ytest = train_test_split(X, y, test_size=0.3, random_state=0)

5、模型训练

# GradientBoostingRegressor(
#     loss='ls',
#     learning_rate=0.1, 
#     n_estimators=100,
#     subsample=1.0,     
#     criterion='friedman_mse',
#     min_samples_split=2,
#     min_samples_leaf=1,
#     min_weight_fraction_leaf=0.0,
#     max_depth=3,
#     min_impurity_decrease=0.0,
#     min_impurity_split=None,
#     init=None,
#     random_state=None,
#     max_features=None,
#     alpha=0.9,
#     verbose=0,
#     max_leaf_nodes=None,
#     warm_start=False,
#     presort='deprecated',
#     validation_fraction=0.1,
#     n_iter_no_change=None,
#     tol=0.0001,
#     ccp_alpha=0.0,
# )

我们把GradientBoostingRegressor的重要参数分为两类，第一类是Boosting框架的重要参数，第二类是弱学习器即CART回归树的重要参数。

GBDT类库boosting框架参数:

• n_estimators: 弱学习器(基学习器)的数量。一般来说，n_estimators太小，容易欠拟合，n_estimators太大，又容易过拟合。默认100。
• learning_rate: 学习率，又叫步长，如果设置太大模型就无法收敛（可能导致很小或者MSE很大的情况），如果设置太小模型速度就会非常缓慢。通常，我们不调整，即便调整，一般它也会在[0.01,0.2]之间变动。如果我们希望模型的效果更好，更多的可能是从树本身的角度来说，对树进行剪枝，而不会寄希望于调整步长。
• subsample: 子采样比例，取值为(0,1]。注意这里的子采样和随机森林不一样，随机森林使用的是放回抽样，而这里是不放回抽样。如果取值为1，则全部样本都使用，等于没有使用子采样。如果取值小于1，则只有一部分样本会去做GBDT的决策树拟合。选择小于1的比例可以减少方差，即防止过拟合，但是会增加样本拟合的偏差，因此取值不能太低。推荐在[0.5, 0.8]之间，默认是1.0，即不使用子采样。
• init: 即我们的初始化的时候的弱学习器，拟合对应原理篇里面的f0(x)，如果不输入，则用训练集样本来做样本集的初始化分类回归预测。否则用init参数提供的学习器做初始化分类回归预测。一般用在我们对数据有先验知识，或者之前做过一些拟合的时候，如果没有的话就不用管这个参数了。
• loss: 即我们GBDT算法中的损失函数。分类模型和回归模型的损失函数是不一样的。对于分类模型，有对数似然损失函数"deviance"和指数损失函数"exponential"两者输入选择。默认是对数似然损失函数"deviance"。在原理篇中对这些分类损失函数有详细的介绍。一般来说，推荐使用默认的"deviance"。它对二元分离和多元分类各自都有比较好的优化。而指数损失函数等于把我们带到了Adaboost算法。对于回归模型，有均方差"ls", 绝对损失"lad", Huber损失"huber"和分位数损失“quantile”。默认是均方差"ls"。一般来说，如果数据的噪音点不多，用默认的均方差"ls"比较好。如果是噪音点较多，则推荐用抗噪音的损失函数"huber"。而如果我们需要对训练集进行分段预测的时候，则采用“quantile”。
• alpha：这个参数只有GradientBoostingRegressor有，当我们使用Huber损失"huber"和分位数损失“quantile”时，需要指定分位数的值。默认是0.9，如果噪音点较多，可以适当降低这个分位数的值。

GBDT类库弱学习器参数:

• max_features：一般来说，如果样本特征数不多，比如小于50，我们用默认的"None"（划分时考虑所有的特征数）就可以了。
• max_depth： 一般来说，数据少或者特征少的时候可以不管这个值。如果模型样本量多，特征也多的情况下，推荐限制这个最大深度，具体的取值取决于数据的分布。常用的可以取值10-100之间。
• min_samples_split： 默认是2.如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值.
• min_samples_leaf：如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。
• min_weight_fraction_leaf：默认是0，就是不考虑权重问题。一般来说，如果我们有较多样本有缺失值，或者分类树样本的分布类别偏差很大，就会引入样本权重，这时我们就要注意这个值了。
• max_leaf_nodes：如果特征不多，可以不考虑这个值，但是如果特征分成多的话，可以加以限制，具体的值可以通过交叉验证得到。
• min_impurity_split：一般不推荐改动。

不管任何参数，都用默认的，我们拟合下数据看看：

gbr = GradientBoostingRegressor(random_state=10)
# 回归模型使用交叉验证cross_val_score默认的score是R2。
cross_val_score(gbr, Xtrain, ytrain, cv=5, scoring='r2').mean()

0.9351560634463129

从结果可以看到，拟合还可以，但还有提升的空间，我们下面看看怎么通过调参提高模型的准确率和泛化能力。

• R2衡量的是1 - 我们的模型没有捕获到的信息量占真实标签中所带的信息量的比例，所以， R2越接近1越好。

• R2可以使用三种方式来调用，一种是直接从metrics中导入r2_score，输入预测值和真实值后打分。第二种是直接从线性回归LinearRegression的接口score来进行调用。第三种是在交叉验证中，输入"r2"来调用.

• 均方误差MSE衡量预测值和实际值的差异，得到的是每个样本量上的平均误差。

• MSE用sklearn专用的模型评估模块metrics里的类mean_squared_error，另一种是调用交叉验证的类cross_val_score并使用里面的scoring参数来设置使用均方误差。

1）n_estimators基分类器数量

为什么不直接用网格搜索寻找最佳参数呢？

• 参数有多个，有的参数是连续型，取值范围很大，如果把所有参数都放进去执行效率比较慢
• 手动调参可以看参数的变化趋势

泛化误差 = 偏差^2 + 方差 + 噪声^2
bias：模型中预测值和真实值之间的差异，模型越准确，偏差越低；
var：衡量模型的稳定性，模型越稳定，方差越低。

range_ = range(10, 1010, 50)
rs = []
var = []
ge = []
for i in range_:
    reg = GradientBoostingRegressor(n_estimators=i, random_state=0)
    cvresult = cross_val_score(reg, Xtrain, ytrain, cv=5)
    # 记录1-偏差
    rs.append(cvresult.mean())
    # 记录方差
    var.append(cvresult.var())
    # 记录泛化误差的可控部分
    ge.append((1-cvresult.mean())**2 + cvresult.var())
# R2最大（偏差最小）时，参数n_estimators的值，对应的方差
print(range_[rs.index(max(rs))], var[rs.index(max(rs))], max(rs))
# 方差最小时，参数n_estimators的值，对应的偏差
print(range_[var.index(min(var))], rs[var.index(min(var))], min(var))
# 偏差最小时，参数n_estimators的值， 对应的偏差、方差
print(range_[ge.index(min(ge))], rs[ge.index(min(ge))], var[ge.index(min(ge))], min(ge))

60 0.002024876765215483 0.936313277476458
10 0.7942980630202685 0.0007085726842073462
60 0.936313277476458 0.002024876765215483 0.006080875391006117

可视化R2(1-偏差)随着树数量的变化趋势。

plt.figure(figsize=(20, 5))
plt.plot(range_, rs, c='red', label='GBR_R2')
plt.legend()
plt.show()

从结果可以看出，参数n_estimators等于60的时候，R2最大，偏差最小，泛化误差最小。但这个范围太大，还需进一步细化学习。

细化学习曲线，找出最佳n_estimators

range_ = range(20, 200, 10)
rs = []
var = []
ge = []
for i in range_:
    reg = GradientBoostingRegressor(n_estimators=i, random_state=0)
    cvresult = cross_val_score(reg, Xtrain, ytrain, cv=5)
    rs.append(cvresult.mean())
    var.append(cvresult.var())
    ge.append((1-cvresult.mean())**2 + cvresult.var())
print(range_[rs.index(max(rs))], var[rs.index(max(rs))], max(rs))
print(range_[var.index(min(var))], rs[var.index(min(var))], min(var))
print(range_[ge.index(min(ge))], rs[ge.index(min(ge))], var[ge.index(min(ge))], min(ge))

60 0.002024876765215483 0.936313277476458
20 0.9136080277188249 0.0012046961880539126
40 0.9359234165834291 0.0018879348131213929 0.005993743355462156

plt.figure(figsize=(20, 5))
plt.plot(range_, rs, c='red', label='GBR_R2')
plt.legend()
plt.show()

为什么不把泛化误差和R2画在一起呢？因为他们两个的值范围相差太大，如果画到一起，他们两个的变化趋势图就不明显了。

plt.figure(figsize=(20, 5))
plt.plot(range_, ge, c='gray', linestyle='-.', label='GBR_E')
plt.legend()
plt.show()

从以上结果可以看出，

• 树的数量提升对模型的影响有极限，最开始，模型的表现会随着树的数量一起提升，但到达某个点之后，树的数量越多，模型的效果会逐步下降，这也说明了暴力增加n_estimators不一定有效果；
• n_estimators等于60时，模型最精确，n_estimators等于40时，模型的泛化误差最低，观察图发现，40和60的泛化误差相差不太大，这个项目里我们选择n_estimators选择60.

树类是天生过拟合的模型，GBR也是很容易过拟合，看看模型在测试集上的表现怎么样，会不会过拟合，过拟合严重不严重。

cross_val_score(GradientBoostingRegressor(n_estimators=60, random_state=0), Xtest, ytest, cv=5).mean()

0.9744364153165174

测试集上的表现比训练集上的表现更好，没有出现预期的过拟合，说明模型的泛化能力比较好，模型基本是又准又稳。模型的准确率还有提升的空间，再调整下其他参数试试。

2）learning_rate步长

range_ = np.linspace(0.001, 1, 50)
cv = []
for i in range_:
    cv.append(
        cross_val_score(
            GradientBoostingRegressor(n_estimators=60, learning_rate=i, random_state=0), Xtrain, ytrain, cv=5).mean())
print(max(cv),range_[cv.index(max(cv))])

0.9373087477995744 0.10293877551020408

plt.figure(figsize=(20, 5))
plt.plot(range_, cv, c='red', linestyle='-.', label='learning_rate')
plt.legend()
plt.show()

从结果可以看出，

• 增加learning_rate对模型的影响也有限，最开始，模型会随着learning_rate的增大而快速提升，但是到达某个点之后，learning_rate增大，模型的效果逐步下降。
• learning_rate等于0.10293877551020408时，模型的准确率有0.001的提升，提升不明显，learning_rate不调整，选择默认的0.1.

3）subsample随机抽样比例

range_ = np.linspace(0.001, 1, 20)
cv = []
for i in range_:
    cv.append(
        cross_val_score(
            GradientBoostingRegressor(n_estimators=60, subsample=i, random_state=0), Xtrain, ytrain, cv=5).mean())
print(max(cv),range_[cv.index(max(cv))])

0.9377894347708191 0.7371052631578947

plt.figure(figsize=(20, 5))
plt.plot(range_, cv, c='red', linestyle='-.', label='subsample')
plt.legend()
plt.show()

从结果可以看出，

• 增加subsample使得模型效果先越来越好再趋于稳定。
• subsample等于0.9377894347708191时，模型的准确率有0.001的提升，提升不明显，0.9377894347708191不调整，选择默认的1.

4）loss损失函数

range_ = ['ls', 'lad', 'huber', 'quantile']
rs = []
var = []
ge = []
for i in range_:
    reg = GradientBoostingRegressor(n_estimators=60, loss=i, random_state=0)
    cvresult = cross_val_score(reg, Xtrain, ytrain, cv=5)
    rs.append(cvresult.mean())
    var.append(cvresult.var())
    ge.append((1-cvresult.mean())**2 + cvresult.var())

pd.DataFrame({'loss':range_, 'r2':rs, 'var':var, 'ge':ge})

	loss	r2	var	ge
0	ls	0.936313	0.002025	0.006081
1	lad	0.940946	0.001695	0.005183
2	huber	0.940849	0.002030	0.005529
3	quantile	0.594232	0.006639	0.171287

从结果可以看出，

• 当loss是lad时，模型的r2最大，方差最低，模型的泛化误差最低，综合考虑用lad替换掉默认值ls。

5）max_depth树的最大深度

range_ = range(1, 20, 1)
rs = []
var = []
ge = []
for i in range_:
    reg = GradientBoostingRegressor(n_estimators=60, loss='lad', max_depth=i, random_state=0)
    cvresult = cross_val_score(reg, Xtrain, ytrain, cv=5)
    rs.append(cvresult.mean())
    var.append(cvresult.var())
    ge.append((1-cvresult.mean())**2 + cvresult.var())
print(range_[rs.index(max(rs))], var[rs.index(max(rs))], max(rs))
print(range_[var.index(min(var))], rs[var.index(min(var))], min(var))
print(range_[ge.index(min(ge))], rs[ge.index(min(ge))], var[ge.index(min(ge))], min(ge))

3 0.0016954362343966239 0.9409462581444764
1 0.9235824099884041 0.0010230022803099283
3 0.9409462581444764 0.0016954362343966239 0.005182780661535442

plt.figure(figsize=(20, 5))
plt.plot(range_, rs, c='red', label='max_depth')
plt.legend()
plt.show()

plt.figure(figsize=(20, 5))
plt.plot(range_, ge, c='gray', linestyle='-.', label='max_depth')
plt.legend()
plt.show()

从结果可以看出，

• max_depth对模型的影响有限，刚开始，max_depth越大模型表现越好，当max_depth达到某一点以后，max_depth增大模型的表现反而下降并波动。
• max_depth等于3时，模型表现最好，泛化误差最低，因为3是max_depth的默认值，因此不调整max_depth，选择它的默认值。

6）min_samples_split内部节点再划分所需最小样本数

range_ = range(2, 20, 1)
rs = []
var = []
ge = []
for i in range_:
    reg = GradientBoostingRegressor(n_estimators=60, loss='lad', min_samples_split=i, random_state=0)
    cvresult = cross_val_score(reg, Xtrain, ytrain, cv=5)
    rs.append(cvresult.mean())
    var.append(cvresult.var())
    ge.append((1-cvresult.mean())**2 + cvresult.var())
print(range_[rs.index(max(rs))], var[rs.index(max(rs))], max(rs))
print(range_[var.index(min(var))], rs[var.index(min(var))], min(var))
print(range_[ge.index(min(ge))], rs[ge.index(min(ge))], var[ge.index(min(ge))], min(ge))

15 0.0015897736983169672 0.9429893567834393
17 0.9424458978306802 0.0015685688257210165
15 0.9429893567834393 0.0015897736983169672 0.004839987138282945

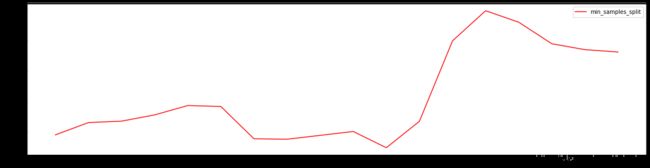
plt.figure(figsize=(20, 5))
plt.plot(range_, rs, c='red', label='min_samples_split')
plt.legend()
plt.show()

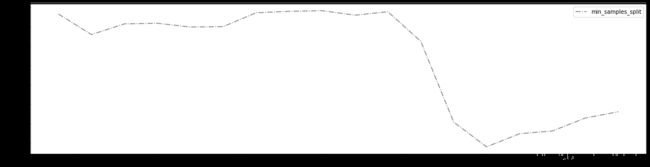
plt.figure(figsize=(20, 5))
plt.plot(range_, ge, c='gray', linestyle='-.', label='min_samples_split')
plt.legend()
plt.show()

从结果可以看出，

• min_samples_split对模型的影响基本是先是积极影响，当min_samples_split达到某一点后就变成消极影响。
• 当min_samples_split等于15时，模型的R2最大，泛化误差最低，模型提升不明显，只提升了0.002，选择不调整min_samples_split。

7）min_samples_leaf叶子节点最少的样本数

range_ = range(1, 20, 1)
rs = []
var = []
ge = []
for i in range_:
    reg = GradientBoostingRegressor(n_estimators=60, loss='lad', min_samples_leaf=i, random_state=0)
    cvresult = cross_val_score(reg, Xtrain, ytrain, cv=5)
    rs.append(cvresult.mean())
    var.append(cvresult.var())
    ge.append((1-cvresult.mean())**2 + cvresult.var())
print(range_[rs.index(max(rs))], var[rs.index(max(rs))], max(rs))
print(range_[var.index(min(var))], rs[var.index(min(var))], min(var))
print(range_[ge.index(min(ge))], rs[ge.index(min(ge))], var[ge.index(min(ge))], min(ge))

18 0.0016066538059972297 0.943714359964585
16 0.9427300239366675 0.0015682135145183393
18 0.943714359964585 0.0016066538059972297 0.004774727080193545

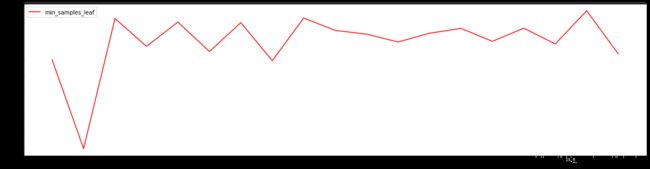
plt.figure(figsize=(20, 5))
plt.plot(range_, rs, c='red', label='min_samples_leaf')
plt.legend()
plt.show()

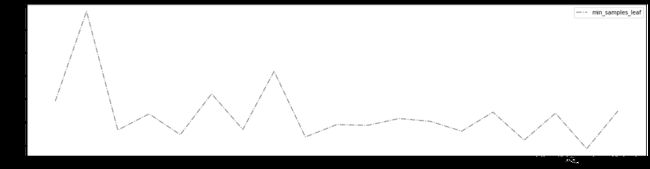
plt.figure(figsize=(20, 5))
plt.plot(range_, ge, c='gray', linestyle='-.', label='min_samples_leaf')
plt.legend()
plt.show()

从结果可以看出，
min_samples_leaf对模型的影响比较复杂，当min_samples_leaf等于18时，模型的R2最大，泛化误差最低，模型提升不明显，只提升了0.003，选择不调整min_samples_leaf。

8) 调参总结

我们选择了7个参数进行调整，最终只选择了2个让模型提升明显的参数：n_estimators 和 loss，最终模型在训练集上的表现和测试集上的表现如下：

reg = GradientBoostingRegressor(n_estimators=60, loss='lad', random_state=0)

cross_val_score(reg, Xtrain, ytrain, cv=5).mean()

0.9409462581444764

cross_val_score(reg, Xtest, ytest, cv=5).mean()

0.9718038505339532

从以上分析可以得出，这个模型的表现还是不错的，具体表现为准确率高、泛化能力强，鲁棒性较好。接下来我们从其他指标来评估模型。

6、模型评估

回归指标评估

为了更好的评估模型效果，我们使用MSE作为回归模型的评估指标。

reg_ = reg.fit(Xtrain, ytrain)
ypred = reg_.predict(Xtest)
reg_.score(Xtest, ytest)

0.9791569249618568

mse_score = mse(ypred, ytest)
mse_score

70668.93448194841

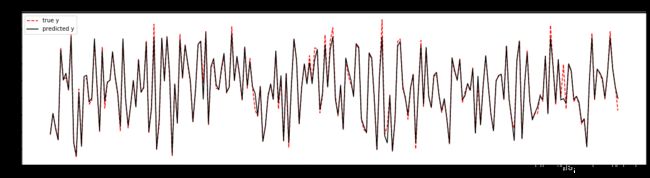
plt.figure(figsize=(20,5))
plt.plot(np.arange(Xtest.shape[0]), ytest, linestyle='--', color='red', label='true y')
plt.plot(np.arange(Xtest.shape[0]), ypred, linestyle='-', color='black', label='predicted y')
plt.title('best model with mse of {0}'.format(int(mse_score)))
plt.legend()

从图形输出结果来看，测试集的预测值（黑色实线）与真实值（红色虚线）的拟合程度比较高。

7、新数据集预测

业务方给了一个新样本数据，针对新数据做预测如下：

New_X = np.array([[1, 1, 0, 1, 15, 0.5, 177, 0.66, 101, 798]])
print(int(reg_.predict(New_X)))

1567

由此得到预测的订单量为1567.

8、GBDT模型的保存和调用

# 保存模型
pickle.dump(reg_, open("gbdtonsales.dat","wb"))
# #注意，open中我们往往使用w或者r作为读取的模式，但其实w与r只能用于文本文件，当我们希望导入的不是文本文件，而
# 是模型本身的时候，我们使用"wb"和"rb"作为读取的模式。其中wb表示以二进制写入，rb表示以二进制读入

# 导入模型
load_model = pickle.load(open("gbdtonsales.dat","rb"))
print('load model from : gbdtonsales.dat')

load model from : gbdtonsales.dat

# 做预测
print(int(load_model.predict(New_X)))

1567

9、项目思考

1. 在这个项目中，不同的自变量之间存在量纲差异，针对这种情况是否需要先对每一列做标准化然后再做回归分析？

• 对回归分析而言，是否做标准化取决于具体场景。这个项目中，回归算法是基于CART的集成模型，量纲本身对于模型没有影响，因此可以不用做标准化。