1.概念：
广度优先搜索算法（Breadth-First-Search），又译作宽度优先搜索，或横向优先搜索，简称BFS，是一种图形搜索算法。简单的说，BFS是从根节点开始，沿着树的宽度遍历树的节点。如果所有节点均被访问，则算法中止。广度优先搜索的实现一般采用open-closed表。
2.解析：
如果说DFS（深度优先搜索）靠的是栈，那BFS（广度优先搜索）靠的就是队列，两种不同的数据结构，反映了这两种搜索的特点。
广度优先搜索的思想：对于无向连通图，广度优先搜索是从图的某个顶点v0出发，在访问v0之后，依次搜索访问v0的各个未被访问过的邻接点w1，w2，…。然后顺序搜索访问w1的各未被访问过的邻接点，w2的各未被访问过的邻接点，…。即从v0开始，由近至远，按层次依次访问与v0有路径相通且路径长度分别为1，2，…的顶点，直至连通图中所有顶点都被访问一次。
我们首先从一个例子入手，看一下这个搜索到底是一个怎么样的过程。
现在我们有一个矩阵表示的图：
0, 1, 0, 0, 1, 0, 0, 0, 0, 0,
1, 0, 1, 1, 0, 0, 0, 0, 0, 0,
0, 1, 0, 0, 0, 0, 1, 0, 0, 0,
0, 1, 0, 0, 1, 1, 0, 0, 0, 0,
1, 0, 0, 1, 0, 0, 0, 0, 1, 0,
0, 0, 0, 1, 0, 0, 1, 1, 0, 0,
0, 0, 1, 0, 0, 1, 0, 0, 0, 1,
0, 0, 0, 0, 0, 1, 0, 0, 1, 1,
0, 0, 0, 0, 1, 0, 0, 1, 0, 0,
0, 0, 0, 0, 0, 0, 1, 1, 0, 0
（卧槽，这TM是人看的么发火）
OK，转换一下，这个图就是这样的一个图（这样就简单易懂了）
由图可以看出，BFS的搜索顺序为1->2->5->3->4->9->7->6->8->10，有点类似于树的层遍历，那么，规则知道了，接下来就是如何变成代码了，当然，我们是通过队列来实现的，这里涉及到队列的两种操作push（）向队尾压入一个元素，empty（），检测队列是否为空，front（）获得队首的元素，pop（）删除队首元素。
那么这个队列到底是怎么工作的呢，往下看
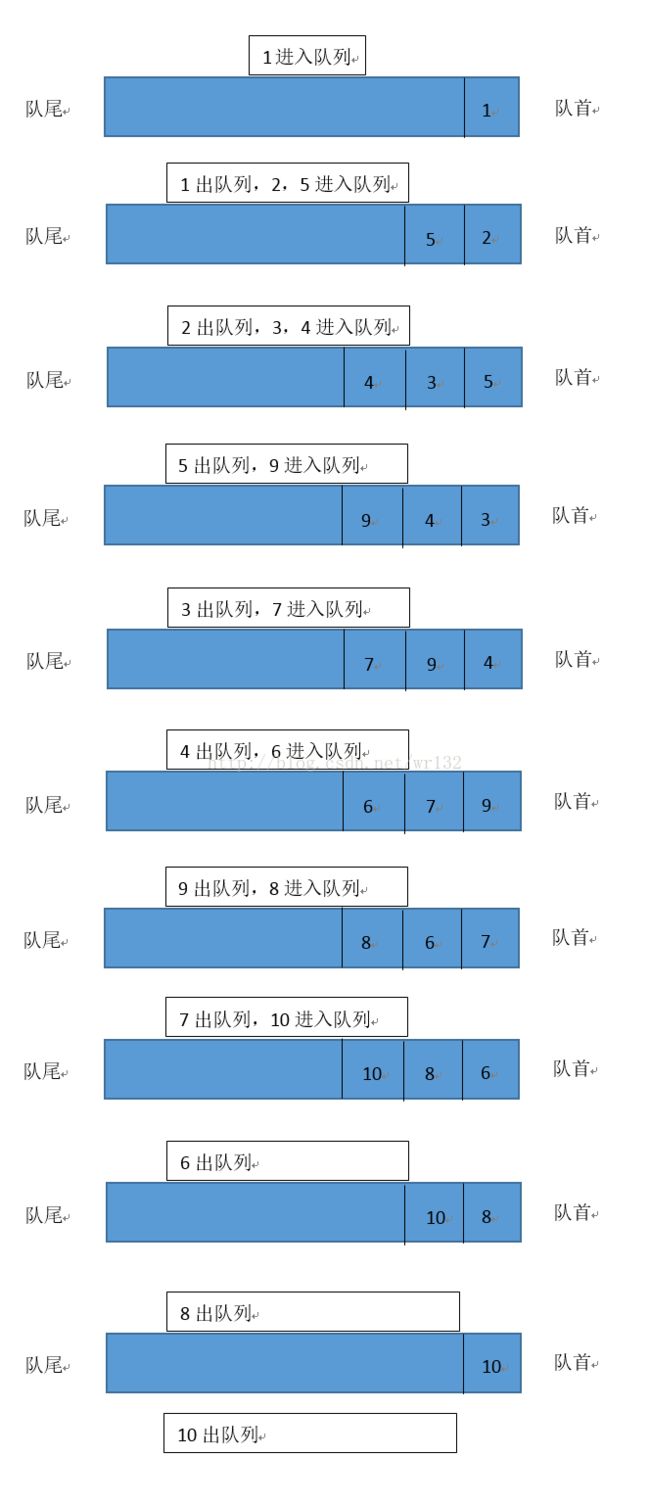
明白了过程，我们再来看代码
算法描述如下：
（1）将起始节点放入队列尾部
（2）While(队列不为空）
**取得并删除**队列首节点Node
处理该节点Node
把Node的**未处理相邻节点加入队列**尾部
使用该算法注意的问题：
（1）使用该算法关键的数据结构为：队列，队列保证了广度渡优先，并且每个节点都被处理到
（2）新加入的节点一般要是未处理过的，所以某些情况下最初要对所有节点进行标记
接下来是实现这个操作的代码：
#include
#include
using namespace std;
//节点数
#define M 10
//图的矩阵表示
int matrix[M][M] =
{ 0, 1, 0, 0, 1, 0, 0, 0, 0, 0,
1, 0, 1, 1, 0, 0, 0, 0, 0, 0,
0, 1, 0, 0, 0, 0, 1, 0, 0, 0,
0, 1, 0, 0, 1, 1, 0, 0, 0, 0,
1, 0, 0, 1, 0, 0, 0, 0, 1, 0,
0, 0, 0, 1, 0, 0, 1, 1, 0, 0,
0, 0, 1, 0, 0, 1, 0, 0, 0, 1,
0, 0, 0, 0, 0, 1, 0, 0, 1, 1,
0, 0, 0, 0, 1, 0, 0, 1, 0, 0,
0, 0, 0, 0, 0, 0, 1, 1, 0, 0
};
//访问标记,初始化为0,
int visited[M + 1];
//graph traverse
void GT_BFS()
{
visited[1] = 1;
queue q;
q.push(1);
while(!q.empty())
{
int top = q.front();
cout << top<<" ";//输出
q.pop();
int i ;
for(i = 1; i <= M; ++i)
{
if(visited[i] == 0 && matrix[top - 1][i - 1 ] == 1)
{
visited[i] = 1;
q.push(i);
}
}
}
}
int main()
{
GT_BFS();//输出结果为1 2 5 3 4 9 7 6 8 10
//system("pause");
return 0;
}