路径规划算法--PRM,从原理到Matlab实现
注: 本篇博客转载自运动规划入门 | 3. 白话PRM,从原理到Matlab实现,老师讲的太好了,我这里转载留存下。
上一回,我们讲完了A的工作原理,与Dijkstar相比A确实有一定程度上的优化,但是我们最后也提到了,即便如此A和Dijkstar一样,依旧还是在逐一遍历地图中的每一个栅格,这对于算法的实际使用是十分不友好的,毕竟我们不可能使用一张2020或者100*100的地图来描述实际的物理世界,往往实际上的地图是会远远大于这个尺寸的。
在座的小伙伴们一定知道在概率统计中,有一个概念叫做抽样调查,对大量的数据进行抽样的话,可以大大地压缩数据量,并且抽样的结果依然可以代表整体的特征。PRM(概率路线图)便是具有相似的原理。PRM就是通过对一张大地图进行稀疏采样,从而将原本很巨大的栅格地图简化为较少的采样点和它们之间的边组成的“无向图”。没错,就是图论意义上的那个图。从而我们可以拿着这张简化了的地图进行路径规划。
- Dijkstar、A*和PRM之间的那点关系
其实在路径规划中,我们把生成一个计划称为“规划阶段”,而依赖规划阶段的结果来找到一条从A到B的路径则称为“查询阶段”。在前两篇中我并未阐明这两者之间的区别,因为在Dijkstar和A中,主要是属于查询阶段,这两个算法都是在执行在A点到B点之间寻找路径这么一件事。而PRM和前者不一样,PRM的主要任务是将原本的栅格地图转化为一张稀疏无向图。而且在后面的介绍中你会发现,实际上PRM和Dijkstar以及A之间并不是互斥的,相反他们经常被结合起来使用,首先由PRM简化地图,然后将简化得到的无向图交给Dijkstar或者A*进行查询。所以他们是各司其职的,并不矛盾。在本文中,我会以Dijkstar为例,展示整套流程。
- PRM是如何运作的?
2.1 基本原理
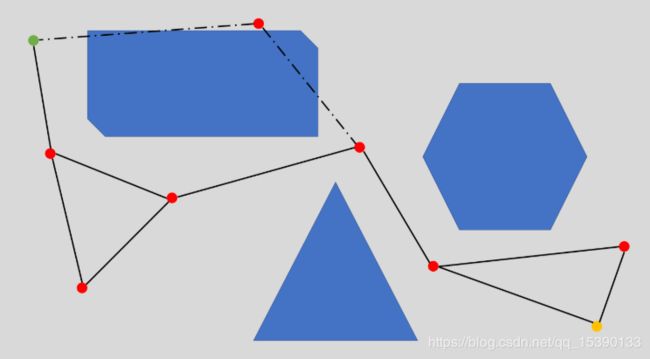
实际上PRM的原理非常好理解,想象着面前有一张平铺的地图,现在我们拿着一堆点往上撒。如下图所示,蓝色几何块代表着障碍物,灰色部分表示自由空间,起初图中只有绿色的起点和黄色的终点,现在我们往地图上撒第一个点,那么显然会有两种可能,一个是很不巧,把点撒在了障碍物上,那么这种情况我们必须要舍弃这个点,重新撒一次,直到我们成功地把点撒到灰色区域。假设这时候我们发现这个点可以连接到起点,于是我们就得到了第一条边。
当我们重复这个过程,不断地往地图上撒点,当然,并不是每一个点都能和相邻的点连接起来的,比如图中的虚线就代表着这两点之间被障碍物阻隔了,这种情况我们就必须舍弃掉这条边
假设我们设置采样点为10个点,那么结果就会得到像下面这样的一张稀疏的无向图。这张无向图即保留了原本栅格地图的特征,而且大大压缩了数据量。
在第一篇中,我在讲解Dijkstar的原理的时候就讲过无向图,并以此为例说明了Dijkstar的运作过程,所以我们知道这种稀疏的无向图其实是对Dijkstar和A*这种规划算法十分友好的,我们将PRM的输出——稀疏无向图,作为输入交给Dijkstar进行规划,很快就能找到从起点到终点之间的最优路径。
2.2 步长限制
在实际的算法实现中,往往我们会添加一个步长的限制,或者叫连接距离限制,比如我们设置将步长限制在10以内,也就是说如果一个点与它的所有相邻点的距离超过10的话,该点就会被算法放弃。在某些场景下我们可能不希望机器一直走大直线,我们希望它的路线更加光滑,那么我们就可以将这个步长限制在一个小范围内,那么最终得到的路径便会是一小段一小段的直线路径连接起来的样子,后期对该路径进行光滑处理,便可以得到一条平滑的路径。
2.3 碰撞检测
碰撞检测是PRM算法中非常非常重要的一环,没有碰撞检测的话,我们将无法正确构建一张避开障碍的无向图。
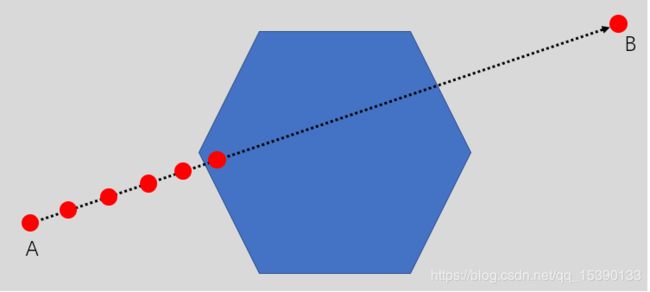
碰撞检测最常见的思路便是:如下图所示,假设我们要对A,B两点之间的连线做碰撞检测,那么我们会对矢量AB进行等距采样,从中挑选出若干个相互等距的采样点,从而逐个检测其是否处于障碍物的位置。至于要从中取多少个采样点,这取决于你对其检测精度的要求。显而易见采样点越多,碰撞检测就越精确,但是当采样点数量到达一定高度后,再往上增加的话,检测精度的提高不再明显,反而会增大计算压力。
- PRM的Matlab实现
3.5 运行效果
在代码中,我为小伙伴们准备了三张不同的地图,你可以通过注释代码来切换地图,看看有什么不同的效果。
11
老样子,我们还是使用那张20*20的实例地图来看看运行效果,这个是采样点为50的时候的运行效果,可以看PRM在栅格地图中不断的选取合理的采样点,最终形成一张稀疏无向图,再交由Dijkstar进行路径查询,最终找到最优路径。
3.6 采样点和步长限制对效果的影响
代码中的PRM_Builder函数就是用于构建概率路线图,可以从下图中看出,由PRM_Builder构建出的路线图graph被输入到dijkstar中进行查询。
其中PRM_Builder有两个重要的参数:sampling_points和step_length_limit。一个代表采样点数量,一个代表步长限制。显然,不同的采样点数量和步长限制必然会对最终的效果产生影响。我们可以通过不同的参数配置来看看具体会产生什么影响。
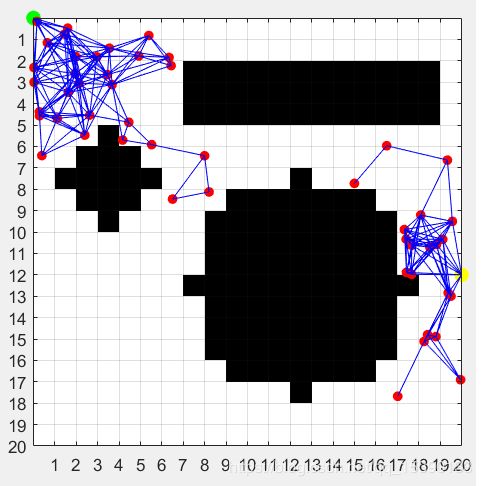
当我们采样点保持在50个,但是将步长限制缩小为3,会发现最终的随机点的分布更加集中,但是由于采样点不够多,导致了规划失败。
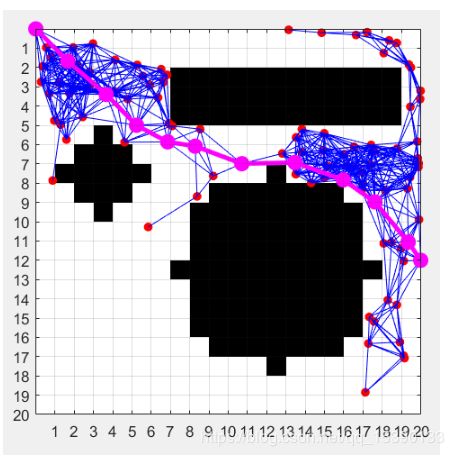
于是我们依旧保持步长限制为3,但是这次增加采样点到100个。可以看到,这次就成功完成了规划。
那么假如我们设置采样点为50个,但是步长限制设置为无穷大,也就是不限制步长的话会怎么样呢?结果就是我们发现随机点的布局非常的肆无忌惮,到处都是。所以我们这就知道了,当步长限制越小时,随机点的分布就会相对更集中,相反步长限制越大的话,分布便会更加分散。

当然,如果你和我一样对自己的电脑性能有自信的话,我还准备了一张100*100的地图,让我们来看看当采样点增加到1000的时候,步长限制为5,会是什么样的。
结果简直是丧心病狂,这个结果算了将近40秒。当然其中很大一部分时间是matlab在连线,如果关掉绘图的话,会快很多。
-
PRM的不足
看起来这么秀的PRM有没有弱点所在呢?当然有。首先,PRM由于其选点的随机性,导致了当他遇到一些狭长的通道时,规划失败的机率会大大上升,比如这样:像这种具有狭长通道的地图,最终规划出来的无向图很容易就会被一分为二,导致找不到从起点到终点的路径
当然,遇到这种情况,可以通过适当增加采样点,以及增大步长限制来增大规划成功的机率
而且同样由于PRM是基于概率的算法,所以会导致每次规划出来的结果都会不一样,这对某些路径一致性要求比较严格的场景来说,PRM可能不是最佳的规划算法: