Apollo学习笔记(6)module control
这几篇都是阅读了各位大神的博客,转载了一部分,以及加上了一些自己的想法,如有侵权,请移步到大神博客自行观看。
研究控制前,先了解一下Apollo项目的整体结构,如下图所示,它包含了感知、定位、决策、控制、通信等几大模块。

其中,Apollo中使用了三种控制算法:
- 纵向 PID
- 横向 LQR
- MPC
其中还包含了一些其他的控制算法,比如,lead/lag 、自适应等,需要一定的控制理论基础的,Apollo中的模型来自这本书 Vehicle Dynamics and Control,另外还需要对 Frenet 坐标系有一定的了解,这些可以自行去查阅相关资料。
纵向控制
纵向控制主要通过控制汽车的刹车/油门来实现对汽车速度的控制。它主要由一个级联控制器和一个标定表构成。
- 级联控制器由 位置PID闭环控制器 和 速度PID闭环控制器 构成;
- 标定表是指 速度-加速度-刹车/油门命令 标定表。
说到底对纵向控制的根本就是对车辆的加速度进行控制,但是每辆车的线控接口都是不一样的,当然有加速度就更完美了,Apollo中使用的Lincoln(我没开发过Lincoln)估计是按照油门踏板、刹车踏板的开度进行车辆控制的,因此就有了标定表,这个表的主要功能就是在不同车速下,油门或者刹车不同开度下,获得车辆的加速度(会取一些比较特殊的点,在使用到标定表中没有的加速度数值时,会对标定表进行二维插值),最终还是用加速度对车辆进行控制。
计算纵向控制的函数:
Status LonController::ComputeControlCommand(
const localization::LocalizationEstimate *localization,
const canbus::Chassis *chassis,
const planning::ADCTrajectory *planning_published_trajectory,
control::ControlCommand *cmd)
输入变量:
- localization 车辆定位,主要包括车辆 x,y,yaw
- chassis 底盘信息,主要包括车辆 v, 前轮转角 angle
- planning_published_trajectory 规划轨迹,规划层给出的规划结果,路点,对应路点上的期望速度,加速度,加速度变化量等其他信息(没做过规划,不是很懂,所以这里就不太多赘述了)
输出变量:
- cmd 车辆的控制信息,Lincoln是油门/刹车,有的接口是加速度,扭矩等,根据实际情况来,这里并不一定就是Apollo的好用
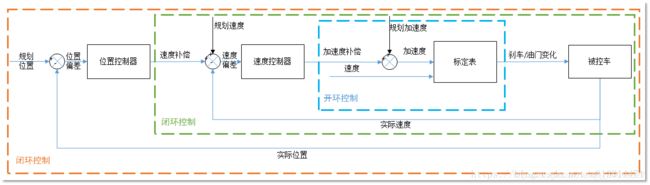
Apollo纵向控制的工作原理框图如下所示:
位置PID闭环控制器
| 模块 | 变量 |
|---|---|
| 输入 | 期望位置+当前实际位置 |
| 输出 | 速度补偿量 |
速度PID闭环控制器
| 模块 | 变量 |
|---|---|
| 输入 | 速度补偿+当前位置速度偏差 |
| 输出 | 加速度补偿量 |
速度-加速度-刹车/油门命令标定表
| 模块 | 变量 |
|---|---|
| 输入 | 加速度补偿+规划加速度,车速 |
| 输出 | 油门/刹车控制量 |
本人理解,Apollo中纵向控制的核心,就是做了双层的PID:
- 控制位置-速度PID:计算出期望速度补偿
- 速度-加速度PID:上一层的期望速度补偿,加上当前的速度误差,PID计算出期望的加速度
- 速度-加速度-刹车/油门命令标定表:这部分是一个开环控制,根据采到的数据,进行一个二维插值后,下发成油门、刹车的控制命令
主要这么做的目的就是为了在保持速度的基础上,能尽量的保持纵向位置的精度,保证停车的精准度。另外,在每个闭环控制的PID,还可以再加上一层 lead/lag 控制,使能方式在配置文件中。
纵向控制中,纵向误差计算部分很重要,
void LonController::ComputeLongitudinalErrors( const TrajectoryAnalyzer *trajectory_analyzer, const double preview_time, SimpleLongitudinalDebug *debug)
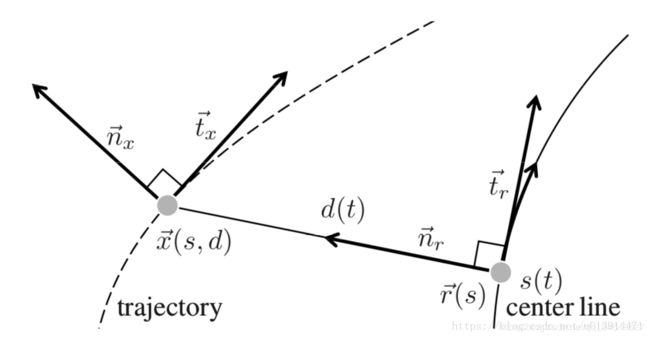
需要对Frenet坐标系有一定的了解
标定表的生成
车辆加速度的标定表生成的方法,参考文档路径:
Apollo/docs/howto/how_to_update_vehicle_calibration.md
并不是所有的车都需要进行这个标定,只有通过油门刹车控制的车辆才需要这个标定,车辆底盘如果有加速度这个控制接口的话,那这个标定表就没有任何意义,控制最重要的思想还是要根据实际情况,调整自己的控制算法,并不是一套就可以通用的。
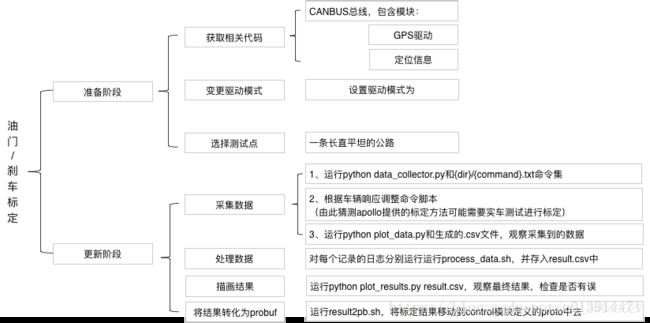
标定流程大致如下:
横向控制
横向控制主要通过调节方向盘转角来实现对航向以及横向偏差的控制。它主要由一个前馈控制器和LQR控制器组成。Apollo中采用车辆模型是动力学模型。
计算纵向控制命令的接口:
Status LatController::ComputeControlCommand(
const localization::LocalizationEstimate *localization,
const canbus::Chassis *chassis,
const planning::ADCTrajectory *planning_published_trajectory,
control::ControlCommand *cmd)
输入变量:
- 定位信息(localization)
- 自车底盘信息(chassis)
- 规划信息(planning_published_trajectory)
输出变量:
- 方向盘控制量(cmd)
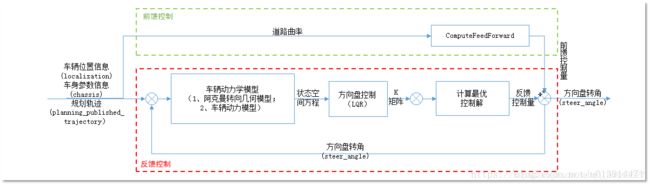
Apollo横向控制的工作原理框图如下所示:
前馈控制器
| 模块 | 变量 |
|---|---|
| 输入 | 道路曲率 |
| 输出 | 方向盘前馈控制量 |
前馈控制量为了补偿道路曲率对稳态误差的影响,实现零稳态误差。
δ f f = L R + K v a y − k 3 [ ℓ r R − ℓ f 2 C a r m V x 2 R ℓ ] \delta_{ff}=\frac{L}{R}+K_{v}a_{y}-k_3[\frac{\ell_r}{R}-\frac{\ell_f}{2C_{ar}}\frac{mV^{2}_{x}}{R\ell}] δff=RL+Kvay−k3[Rℓr−2CarℓfRℓmVx2]
反馈控制器
| 模块 | 变量 |
|---|---|
| 输入 | 期望航向角,横向偏差 |
| 输出 | 方向盘反馈控制量 |
LQR控制器的主要公式:
d d t [ e 1 e 1 ˙ e 2 e 2 ˙ ] = [ 0 1 0 0 0 − 2 C a f + 2 C a r m V x 2 C a f + 2 C a r m − 2 C a f ℓ f + 2 C a r ℓ r m V x 0 0 0 1 0 − − 2 C a f ℓ f − 2 C a r ℓ r I z V x 2 C a f ℓ f − 2 C a r ℓ r I z − 2 C a f ℓ f 2 + 2 C a r ℓ r 2 I z V x ] [ e 1 e 1 ˙ e 2 e 2 ˙ ] + [ 0 2 C a f m 0 2 C a f ℓ f I z ] δ + [ 0 − 2 C a f ℓ f − 2 C a r ℓ r m V x − V x 0 − 2 C a f ℓ f 2 + 2 C a r ℓ r 2 I z V x ] ψ ˙ d e s \frac{d}{dt} \begin{bmatrix} e_1 \\ \dot{e_1} \\ e_2 \\ \dot{e_2} \\ \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 &-\frac{2C_{af}+2C_{ar}}{mV_x} & \frac{2C_{af}+2C_{ar}}{m} & \frac{-2C_{af}\ell_f+2C_{ar}\ell_r}{mV_x} \\ 0 & 0 & 0 & 1 \\ 0 &-\frac{-2C_{af}\ell_f-2C_{ar}\ell_r}{I_zV_x} & \frac{2C_{af}\ell_f-2C_{ar}\ell_r}{I_z} & -\frac{2C_{af}\ell^2_f+2C_{ar}\ell^2_r}{I_zV_x} \\ \end{bmatrix} \begin{bmatrix} e_1 \\ \dot{e_1} \\ e_2 \\ \dot{e_2} \\ \end{bmatrix} \\ +\begin{bmatrix} 0 \\ \frac{2C_{af}}{m} \\ 0 \\ \frac{2C_{af}\ell_f}{I_z} \\ \end{bmatrix} \delta + \begin{bmatrix} 0 \\ -\frac{2C_{af}\ell_f-2C_{ar}\ell_r}{mV_x}-V_x \\ 0 \\ -\frac{2C_{af}\ell^2_f+2C_{ar}\ell^2_r}{I_zV_x} \\ \end{bmatrix} \dot{\psi}_{des} dtd⎣⎢⎢⎡e1e1˙e2e2˙⎦⎥⎥⎤=⎣⎢⎢⎢⎡00001−mVx2Caf+2Car0−IzVx−2Cafℓf−2Carℓr0m2Caf+2Car0Iz2Cafℓf−2Carℓr0mVx−2Cafℓf+2Carℓr1−IzVx2Cafℓf2+2Carℓr2⎦⎥⎥⎥⎤⎣⎢⎢⎡e1e1˙e2e2˙⎦⎥⎥⎤+⎣⎢⎢⎡0m2Caf0Iz2Cafℓf⎦⎥⎥⎤δ+⎣⎢⎢⎢⎡0−mVx2Cafℓf−2Carℓr−Vx0−IzVx2Cafℓf2+2Carℓr2⎦⎥⎥⎥⎤ψ˙des
闭环控制主要结合车辆动力学模型得出状态矩阵,然后利用LQR模型获取K矩阵,进而计算最优控制解steer_angle_feedback,它的实现过程如下:
-
依据阿克曼转角几何和车辆动力学原理,搭建车辆动力学模型,列写状态空间方程;
-
根据已知车辆信息,计算横向偏差,更新状态矩阵、状态矩阵系数、控制矩阵系数等;
更新状态矩阵,代码对应接口:
void LatController::UpdateStateAnalyticalMatching(SimpleLateralDebug *debug)
输入: debug,包含横向误差、航向误差等信息
输出:更新状态矩阵
计算横向误差,代码对应接口:
double LatController::ComputeLateralErrors(
const double x,
const double y,
const double theta,
const double linear_v,
const double angular_v,
const TrajectoryAnalyzer &trajectory_analyzer,
SimpleLateralDebug *debug)
输入:当前车辆位置坐标(x, y)、当前航向角theta、当前线速度linear_v、当前角速度angular_v、规划轨迹trajectory_analyzer
输出:debug信息,主要为生成状态矩阵,状态矩阵包含:lateral_error、lateral_error_rate、heading_error、heading_error_rate四个元素
更新状态矩阵系数matrix_a_和离散状态矩阵系数matrix_ad_,代码对应接口:
void LatController::UpdateMatrix()
更新混合状态矩阵系数matrix_adc_和混合控制矩阵系数matrix_bdc_,代码对应接口:
void LatController::UpdateMatrixCompound()
- 计算K矩阵;
代码对应接口:
void common::math::SolveLQRProblem(
const Matrix &A,
const Matrix &B,
const Matrix &Q,
const Matrix &R,
const double tolerance,
const uint max_num_iteration,
Matrix *ptr_K)
输入:状态矩阵系数A、控制矩阵系数B、控制权重矩阵R、状态权重矩阵Q、迭代次数max_num_iteration、计算阈值tolerance
输出:增益矩阵ptr_K
- 计算最优控制解。
const double steer_angle_feedback = -(matrix_k_ * matrix_state_)(0, 0) * 180 / M_PI * steer_transmission_ratio_/ steer_single_direction_max_degree_ * 100;
反馈量:steer_angle = steer_angle_feedback + steer_angle_feedforward,即为方向盘控制量。