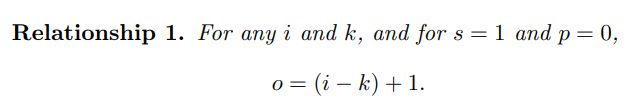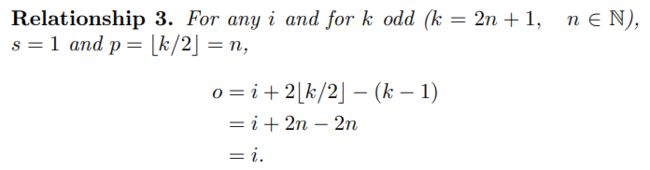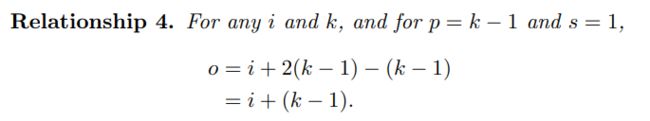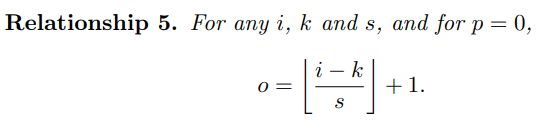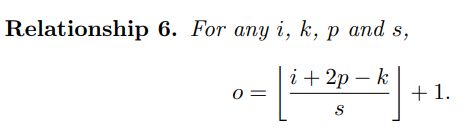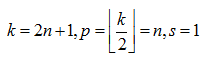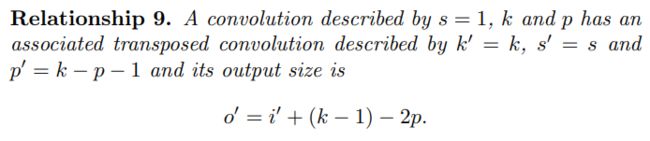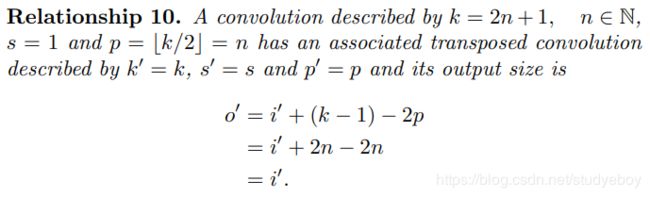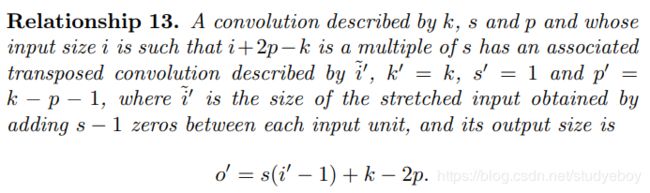卷积-转置卷积-空洞卷积-深度可分离卷积-分组卷积-可变形卷积
卷积
卷积层的结构参数
- 卷积核大小（Kernel Size）：定义卷积操作的感受野。
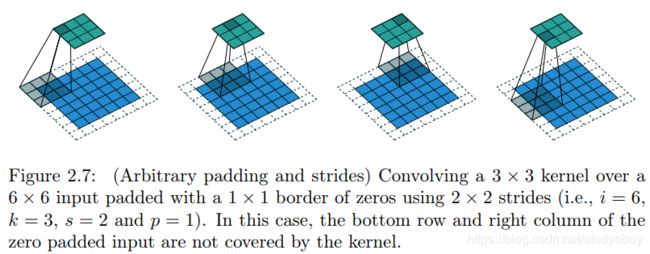
- 步幅（Stride）：定义卷积核遍历图像时的步幅大小。其默认值通常设置为1。设置大于1的值后对图像进行下采样，这种方式类似池化操作。
- 边界扩充（Padding）：定义了网络层处理样本边界的方式。当卷积核大于1且不进行边界扩充，输出尺寸将相应缩小；当卷积核以标准方式进行边界扩充，则输出数据的空间尺寸将与输入相等。
- 输入与输出通道（Channels）：构建卷积层时需定义输入通道 I I I，并由此确定输出通道 O O O。这样，可算出每个我拿过来层的参数量 I × O × K I \times O \times K I×O×K，其中 K K K为卷积核的参数个数。例如，某个网络层有64个大小为 3 × 3 3 \times 3 3×3的卷积核，则对应 K K K值为 3 × 3 = 9 3 \times 3 = 9 3×3=9。
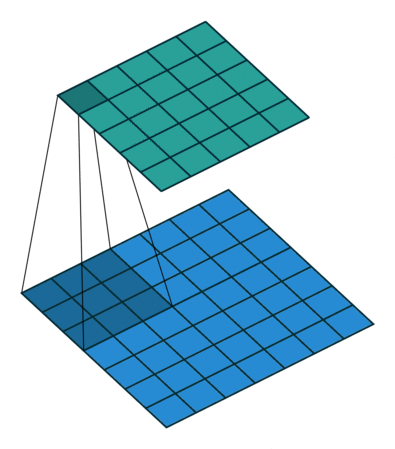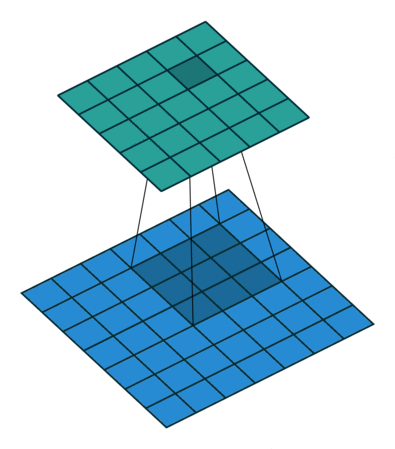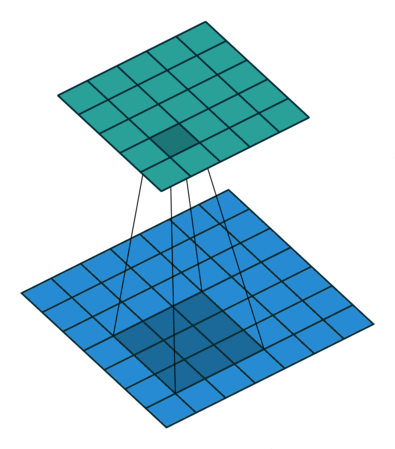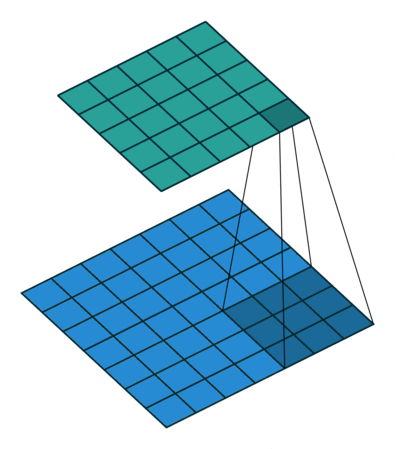
卷积实际上是 加权叠加，输出的维度小于输人的维度。如果需要输出的维度和输入的维度相等，就需要填充（padding）。
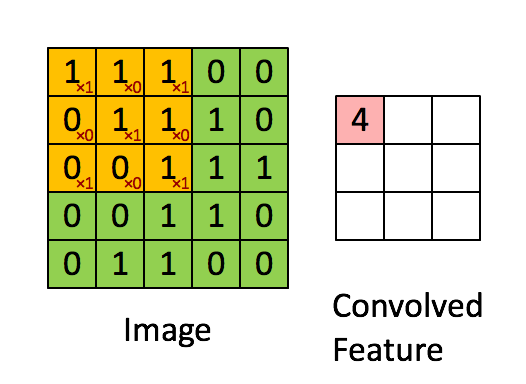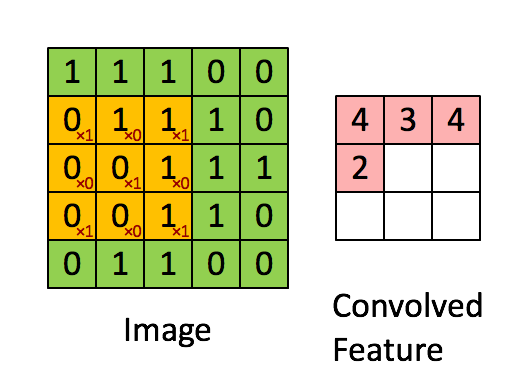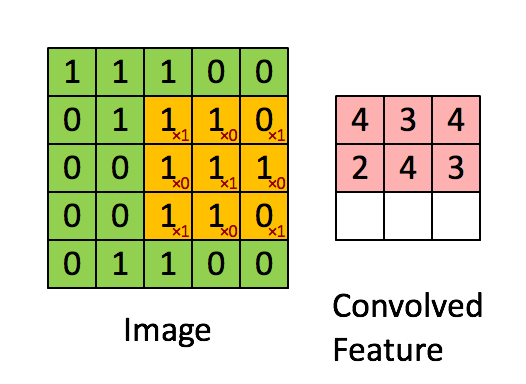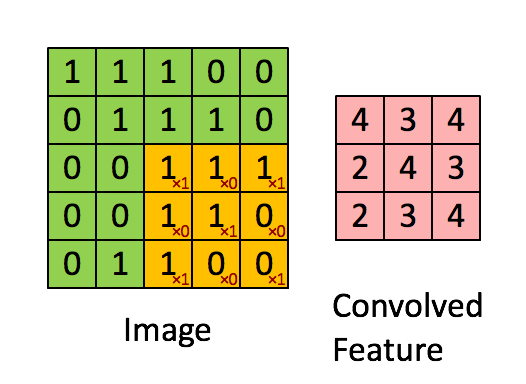
计算公式
o = i + 2 p − k s + 1 o=\frac{i + 2p - k}{s} + 1 o=si+2p−k+1
i：输入图像尺寸
o：输出特征图尺寸
k：卷积核kernel尺寸
p：填充数padding大小
s：步长大小
特殊卷积
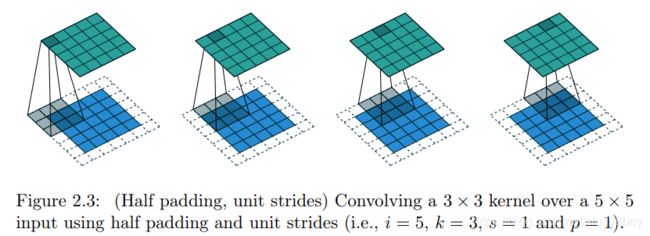
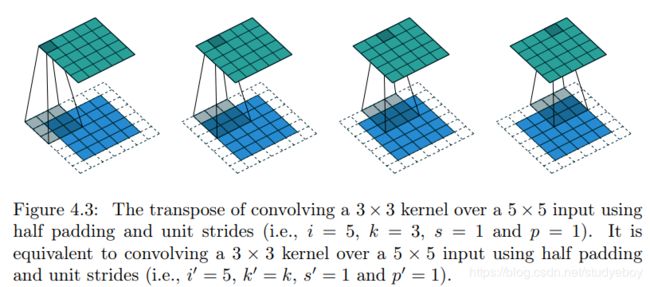
- 输出尺寸和输入尺寸相同（half（same） padding）
当input的维度和output的维度相同时，这种padding叫作same padding。同时也叫作half padding。当进行 k / 2 k/2 k/2的padding时，同时如果 k k k是奇数 （ 2 n + 1 ） （2n+1） （2n+1），则通过推导可知output维度=input维度。
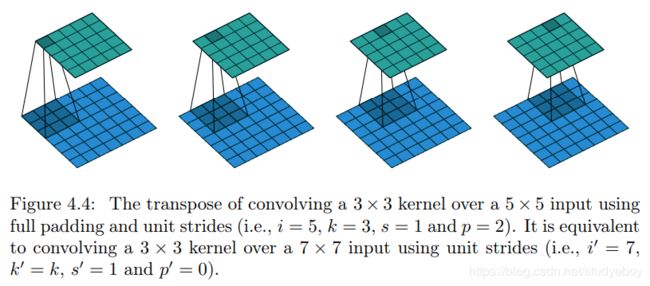
o = ( i − k ) + 2 p + 1 = i + 2 ⌊ k 2 ⌋ − ( k − 1 ) = i + 2 ⌊ 2 n + 1 2 ⌋ − ( 2 n + 1 − 1 ) = i + 2 n − 2 n = i \begin{aligned} o & = (i - k) + 2p + 1 \\ & = i + 2 \lfloor \frac {k}{2} \rfloor - (k - 1) \\ & = i + 2 \lfloor \frac{2n+1}{2} \rfloor - (2n + 1 - 1) \\ & = i + 2n - 2n \\ & = i \end{aligned} o=(i−k)+2p+1=i+2⌊2k⌋−(k−1)=i+2⌊22n+1⌋−(2n+1−1)=i+2n−2n=i - 输出尺寸比输入尺寸大（full padding）
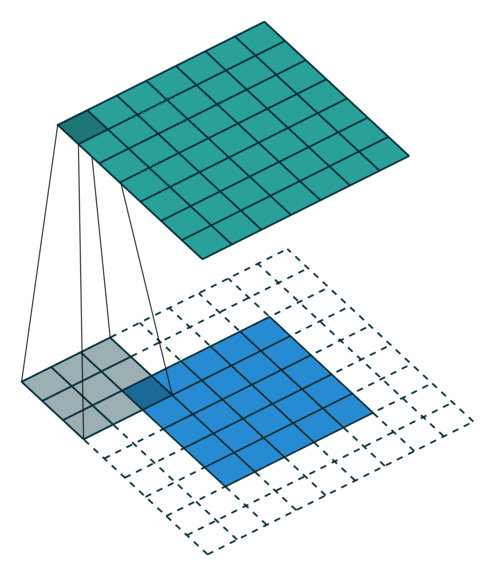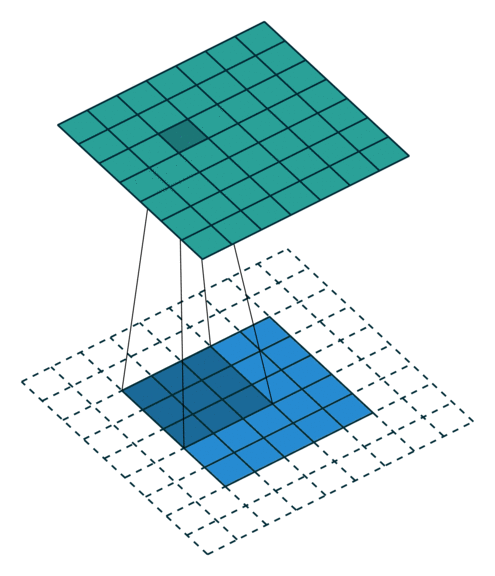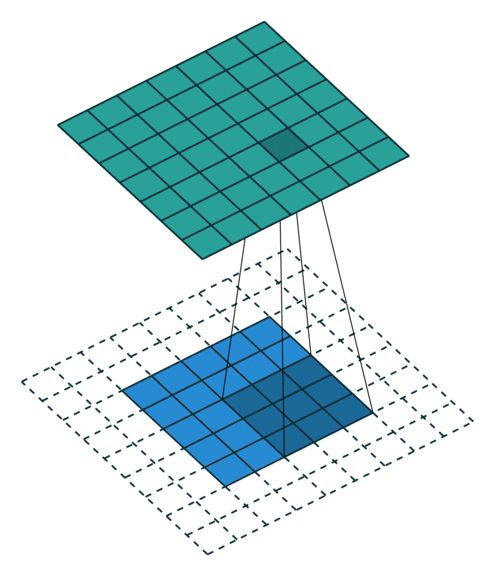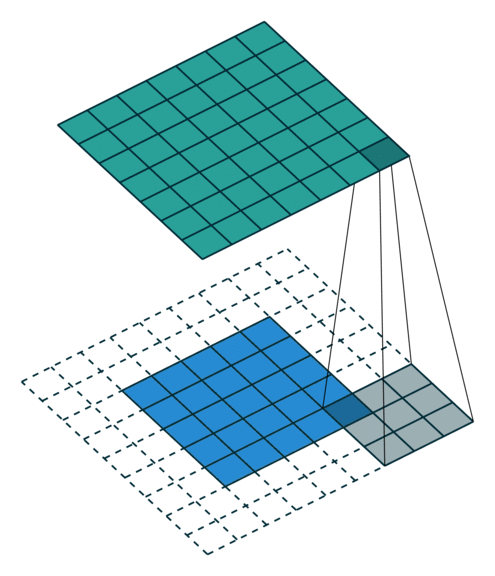
一般的卷积相对于输入大小会减小输出大小，通过适当的零填充可以使输出尺寸大于输入尺寸，这种卷积方法称为全填充，考虑了内核在输入特征图上的部分重叠和完全重叠。当进行 p = k − 1 p = k - 1 p=k−1填充时，输出维度为：
o = i + 2 ( k − 1 ) − k + 1 = i + 2 ( k − 1 ) − ( k − 1 ) = i + ( k − 1 ) \begin{aligned} o & = i + 2(k - 1) - k +1 \\ & = i + 2(k - 1) - (k - 1) \\ & = i + (k - 1) \end{aligned} o=i+2(k−1)−k+1=i+2(k−1)−(k−1)=i+(k−1)
卷积的矩阵表示
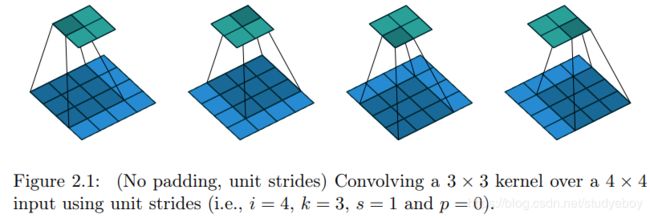
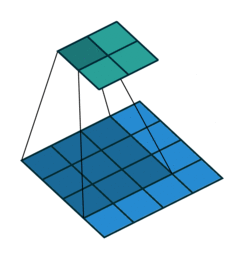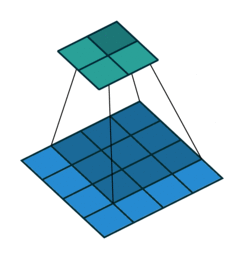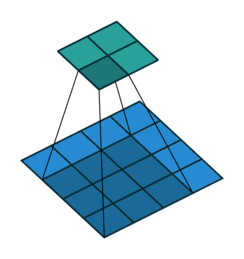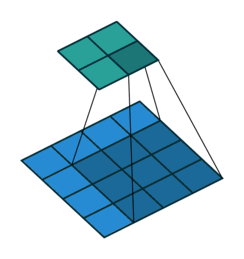
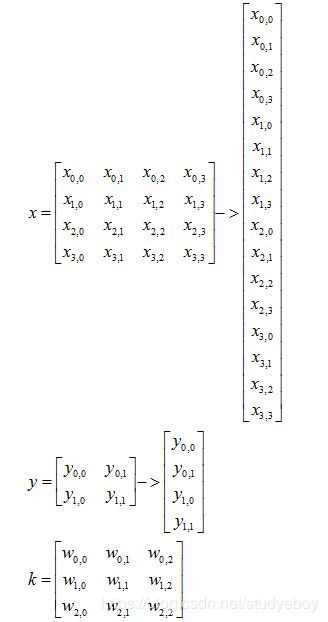
假设一个卷积操作，输入 4 × 4 4 \times 4 4×4， 卷积核大小 3 × 3 3 \times 3 3×3， 步长 1 × 1 1 \times 1 1×1， 填充方式为Valid的情况下，输出则为 2 × 2 ( 2 = 4 − 3 1 + 1 ) 2 \times 2(2 = \frac{4 - 3}{1} + 1) 2×2(2=14−3+1)。我们将其从左往右，从上往下的方式展开：
- 输入矩阵可以展开成维数为[16,1]的矩阵，记作 x x x
- 输出矩阵可以展开成维数为[4, 1]的矩阵，记作 y y y
- y y y要想完成[16,1]到[4, 1]的映射，卷积核可以表示为[4,16]的矩阵，记作C，其中非0的值表示 卷积对应的第 i i i行 j j j列的权重。
- 所以卷积可以用 y = C ∗ x ( [ 4 , 1 ] = [ 4 , 16 ] ∗ [ 16 , 1 ] ) y = C * x([4, 1] = [4, 16] * [16, 1]) y=C∗x([4,1]=[4,16]∗[16,1])来表示。
卷积过程： y = C ∗ x y=C*x y=C∗x
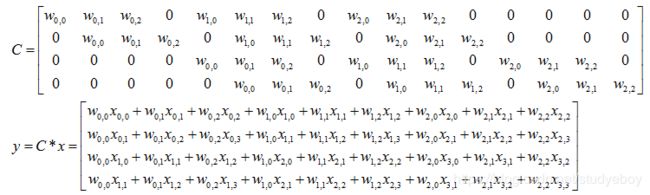
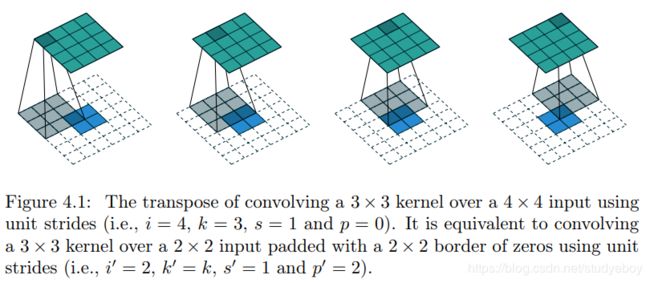
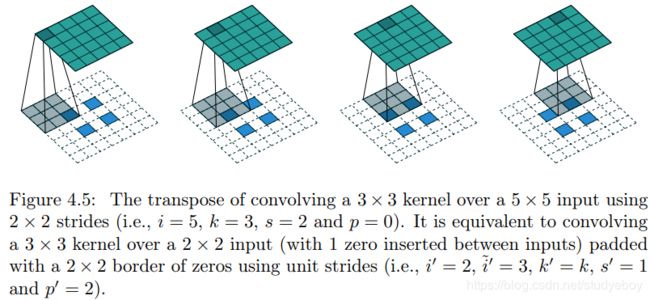
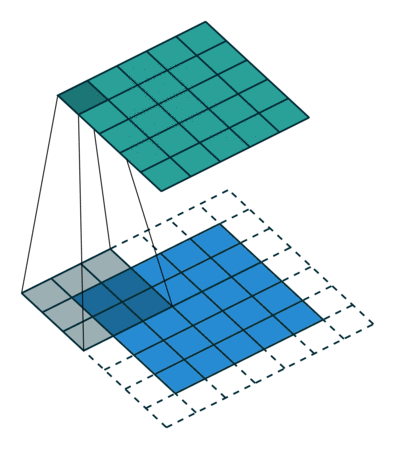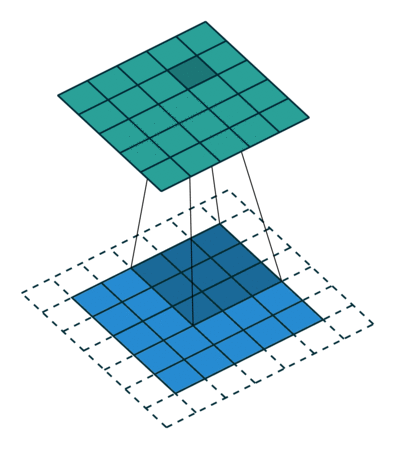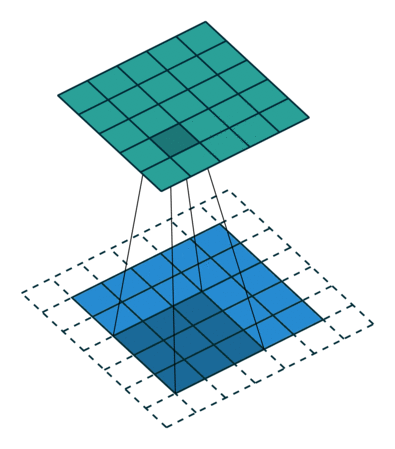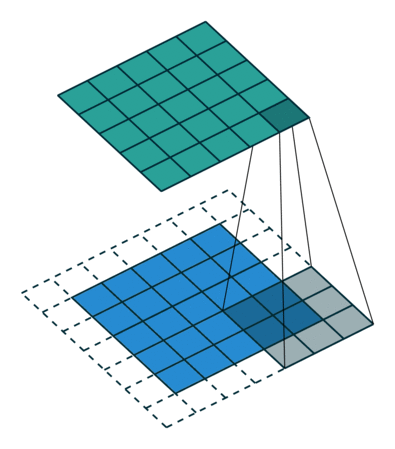
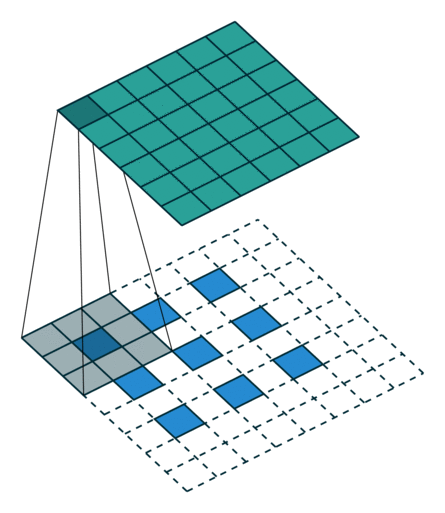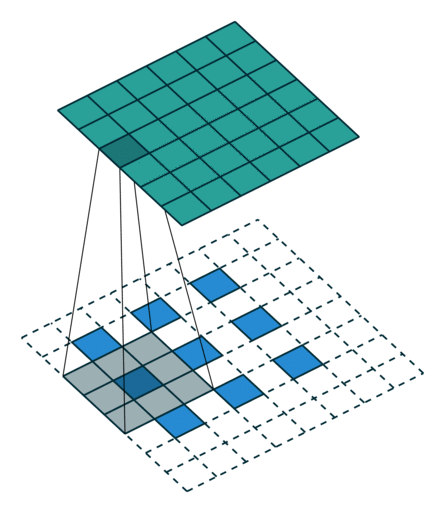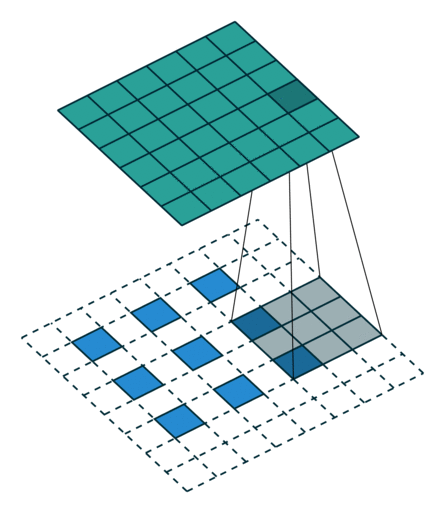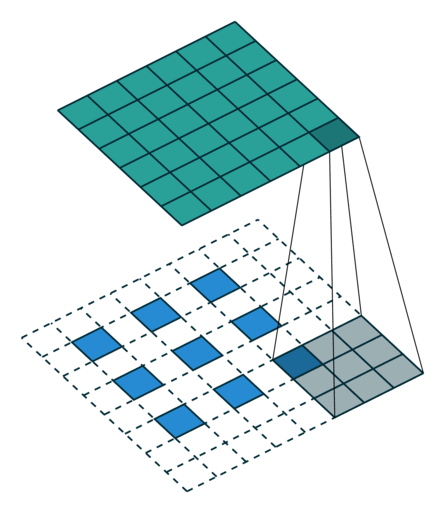
转置（反）卷积
概念
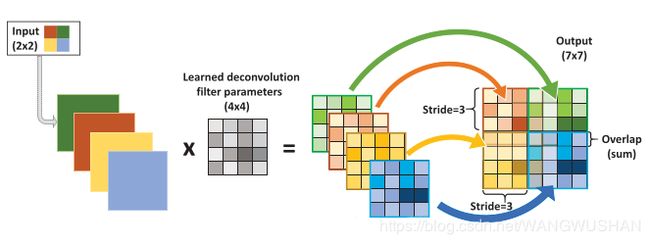
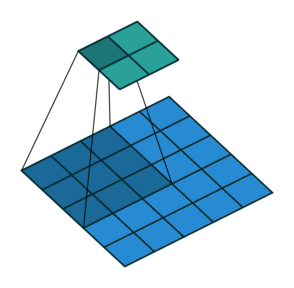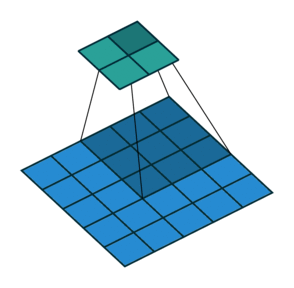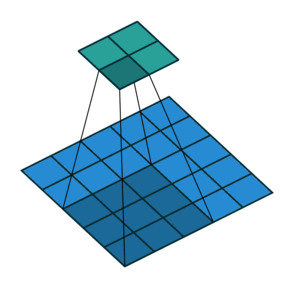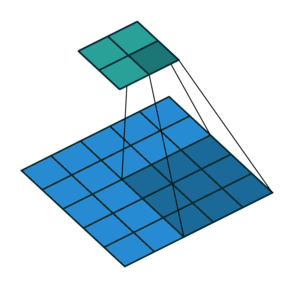
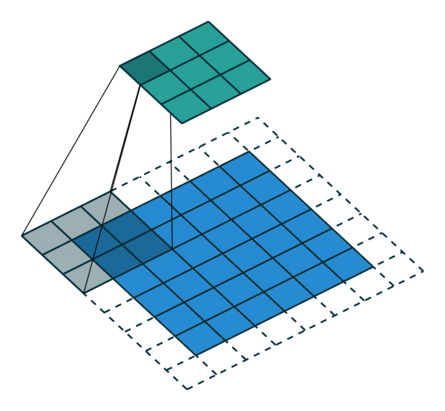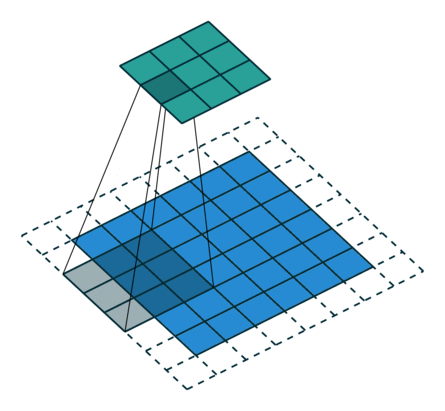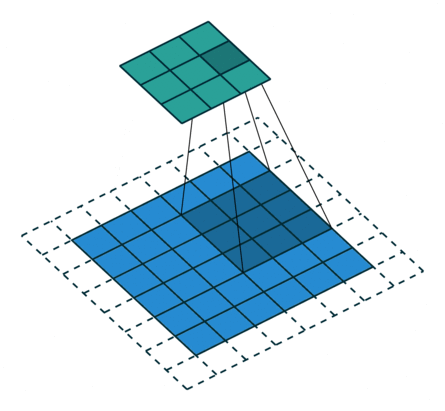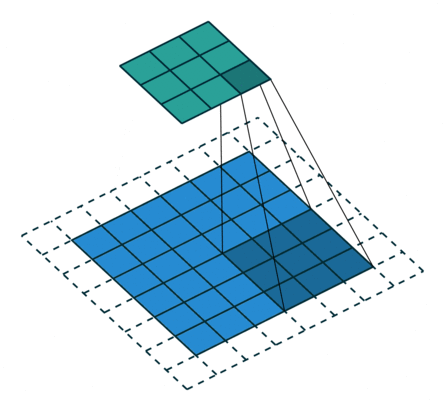
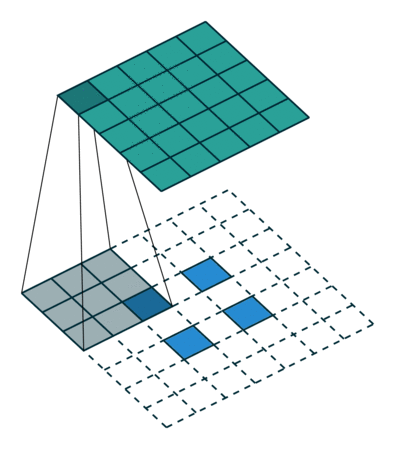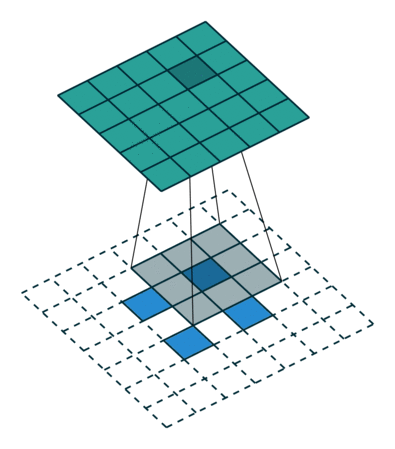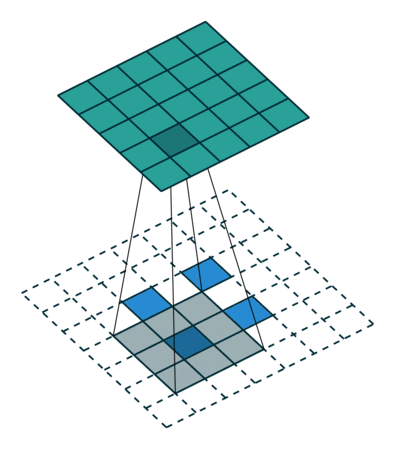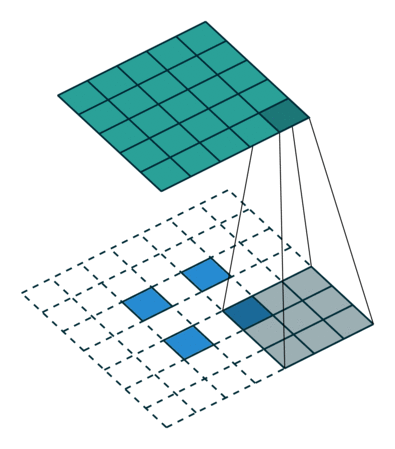
转置卷积（transposed convolutions）又名反卷积（deconvolutions）或是分数步长卷积（fractially straced convolutions）。反卷积的概念第一次出现在Zeiler在2010年发表的论文Deconvolutional Networks中。
深度学习中的deconv是一种上采样upsampling过程，可以还原图像的大小形状，但是不能够完全恢复原来的像素值，因此并不是严格的逆运算。
反卷积从字面上理解就是卷积的逆过程。反卷积虽然存在，但是在深度学习中并不常用。而转置卷积虽然又名反卷积，却不是真正意义上的反卷积。因为根据反卷积的数学含义，通过反卷积可以将通过卷积的输出信号，完全还原输入信号。而事实上，转置卷积智能还原shape大小，而不能还原value。至少在数值方面上，转置卷积不能实现卷积操作的逆过程。所以转置卷积与真正的反卷积有点相似，因为两者产生了相同的空间分辨率。
计算公式
o = s ∗ ( i − 1 ) − 2 p + k o=s * (i - 1) - 2p + k o=s∗(i−1)−2p+k
转置卷积计算公式和卷积公式是可以互推的。
i：输入图像尺寸
o：输出特征图尺寸
k：卷积核kernel尺寸
p：填充数padding大小
s：步长大小
矩阵运算
对应上面卷积的运算的转置运算为： x = C T ∗ y x=C^T*y x=CT∗y
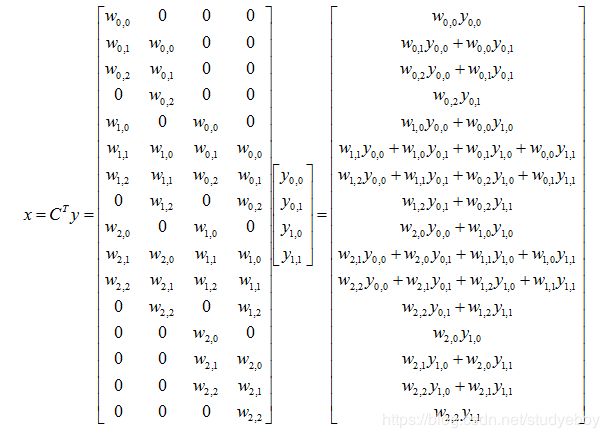
转置卷积应用领域
- CNN可视化，通过转置卷积将卷积得到的feature map还原到像素空间，来观察feature map对哪些pattern响应最大，即可视化哪些特征是卷积操作提取出来的；
- FCN全卷积网络中，由于要对图像进行像素级分割，需要将图像尺寸还原到原来的大小，类似upsampling的操作，所以需要采用转置卷积；
- GAN对抗式生成网络中，由于需要从输入图像到生成图像，自然需要将提取的特征图还原到和原图同样尺寸的大小，即也需要转置卷积操作。
卷积和转置卷积总结
| cases | no padding, no strides | arbitrary padding, no strides | half (same) padding, no strides | full padding, no strides | no padding, strides | padding, strides | padding, strides (odd) |
|---|---|---|---|---|---|---|---|
| conv |  |
 |
 |
 |
 |
 |
|
| fixed parameter |  |
 |
 |
 |
 |
||
| conv e.g. |  |
 |
 |
 |
 |
 |
 |
| conv animation |  |
 |
 |
 |
 |
 |
 |
| transposed conv |  |
 |
 |
 |
 |
 |
 |
| fixed parameter |  |
 |
 |
 |
 |
 |
 |
| transposed conv e.g. |  |
 |
 |
 |
 |
 |
 |
| tansposed conv animation |  |
 |
 |
 |
 |
 |
 |
空洞（扩张）卷积
概念
空洞卷积（atrous convolutions）又名扩张卷积（dilated convolutions），在ICLR 2016上提出，其主要作用是在不增加参数和模型复杂度的条件下，可以指数倍的扩大视觉感受野（每一个输出是由诗句感受野大小的输入决定的）的大小。是针对图像语义分割问题中下采样会降低图像分辨率、丢失信息而提出的一种卷积思路。利用添加空洞扩大感受野，向卷积层引入了一个称为“扩张率（dilate rate）”的超参数，该参数定义了卷积核处理数据时各值的间距。
空洞卷积是对卷积核的操作，这样可以在参数数量不变的情况下，具有更大的感受野。空洞卷积常用在图像分割中。
空洞卷积诞生于图像分割领域，图像输入到网络中经过CNN提取特征，再经过pooling降低图像尺度的同时增大感受野。由于图像分割是pixel-wise预测输出，所以还需要通过upsampling将变小的图像恢复到原始大小。upsampling通常是通过deconv（转置卷积）完成。因此图像分割FCN有两个关键步骤：池化操作增大感受野，upsampling操作扩大图像尺寸。虽然经过upsampling操作恢复了大小，但是很多细节还是被池化操作丢失了。Dilated Conv可满足既增大感受野又不减小图像大小的操作。
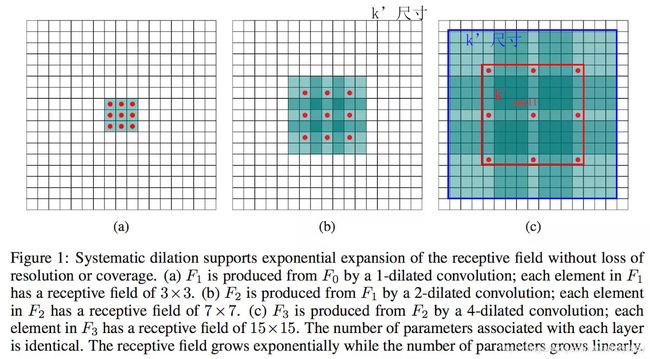
空洞卷积可以简单的理解为，产生了新的kernel，再用这个kernel去做卷积。
计算公式
- 膨胀后的新卷积核大小计算
k ′ = k + ( d − 1 ) ∗ ( k + 1 ) k' = k + (d - 1)*(k + 1) k′=k+(d−1)∗(k+1)
k’：卷积核加空洞膨胀后的卷积核尺寸
d：膨胀系数
k s m a l l ′ = k + ( d − 1 ) ∗ ( k − 1 ) k'_{small} = k + (d - 1)*(k - 1) ksmall′=k+(d−1)∗(k−1)
k’：卷积核加空洞膨胀后的卷积核尺寸
d：膨胀系数
- 空洞卷积后输出图像尺寸
o = i + 2 p − k − ( k − 1 ) ∗ ( d − 1 ) s + 1 o = \frac{i + 2p - k - (k - 1)*(d - 1)}{s} + 1 o=si+2p−k−(k−1)∗(d−1)+1
相当于在普通卷积的基础上增加了一项 ( k − 1 ) ∗ ( d − 1 ) (k - 1)*(d - 1) (k−1)∗(d−1)
i：输入图像尺寸
o：输出特征图尺寸
k：卷积核kernel尺寸
p：填充数padding大小
s：步长大小
d：膨胀系数
空洞卷积总结
| effective kernel | relationship | dilated conv e.g. | animation |
|---|---|---|---|
 |
 |
 |
 |
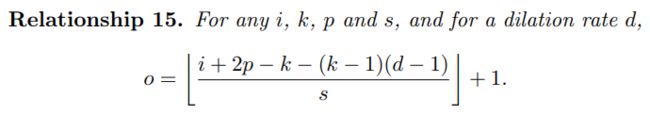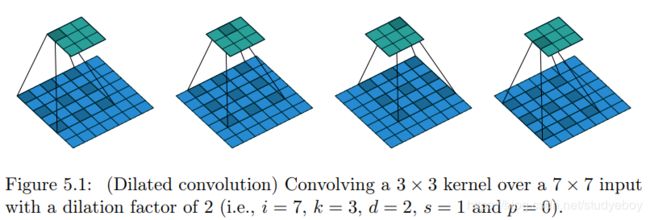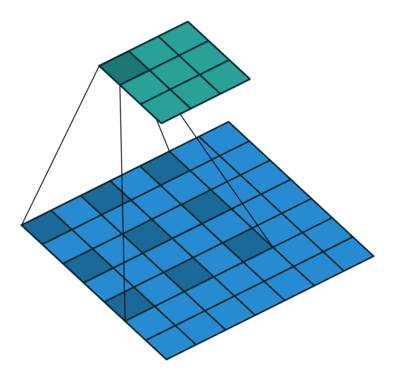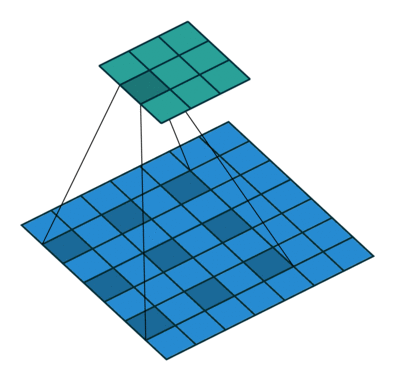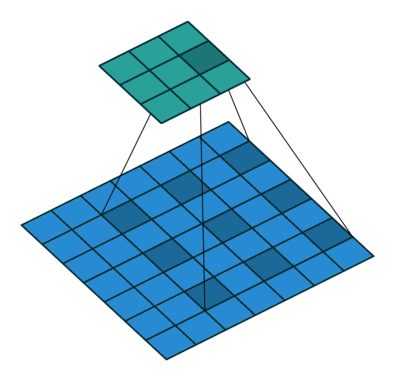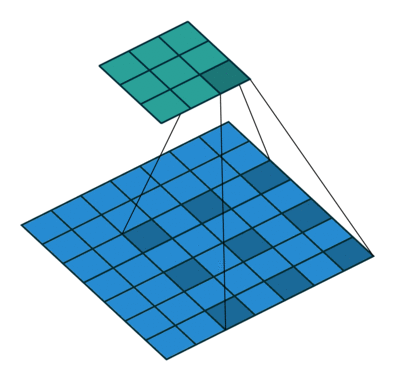可分离卷积（separable convolution）
在可分离卷积（separable convolution）中，可将卷积核操作拆分成多个步骤。卷积操作用 y = c o n v ( x , k ) y = conv(x,k) y=conv(x,k)来表示，其中输出图像为 y y y，输入图像为 x x x，卷积核为 k k k。假设 k k k可由下式计算得出： k = k 1 . d o t ( k 2 ) k = k_{1}.dot(k_{2}) k=k1.dot(k2)。这就实现了一个可分离卷积操作，因为不用 k k k执行二维卷积操作，而是通过 k 1 k_{1} k1和 k 2 k_{2} k2分别实现两次一维卷积来取得相同效果。
Sobel算子通常被用于图像处理中，可以分别乘以矢量[1, 0, -1]和[1, 2, 1]的转置矢量后得到相同的滤波器。完成这个操作，只需要6个参数，而不是二维卷积中的9个参数。
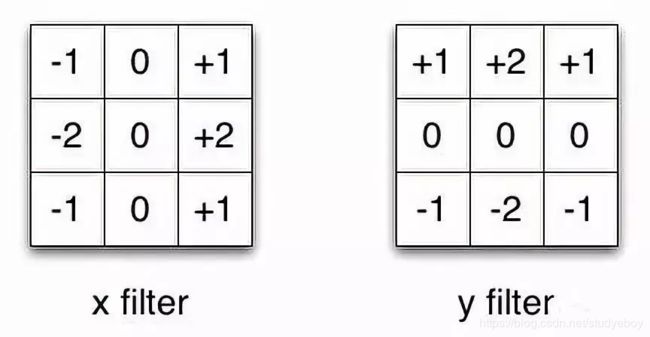
这个例子说明了什么叫做空间可分离卷积，这种方法并不应用在深度学习中，只是帮助理解这种结构。
深度可分离卷积（depthwise separable convolution）
概念
- 传统标准卷积：
同时考虑了图像的区域和通道，即一个卷积核需要对所有的通道进行相同的卷积操作，然后再进行加和，最后得到这个卷积核的一个输出。假设有一个 3 × 3 3 \times 3 3×3的卷积层，输入通道数为16，输出通道数为32，每个卷积核同16个输入通道数据分别卷积，然后叠加每一个通道对应位置的值，得到一个通道上的数据，那么32输出通道数需要 3 × 3 × 16 × 32 = 4608 3 \times 3 \times 16 \times 32 = 4608 3×3×16×32=4608个参数。 - 深度可分离卷积：
深度可分离卷积的成功应用是Google的Xception网络。首先对每一个通道进行各自的卷积操作，有多少个通道就有多少个过滤器。得到新的通道feature map后，再对这些通道feature map进行标准的 1 × 1 1 \times 1 1×1跨通道卷积操作。针对上面的例子应用深度可分离卷积，用1个 3 × 3 3 \times 3 3×3大小的卷积核遍历16个通道的数据，得到16个特征图，然后用32个 1 × 1 1 \times 1 1×1的卷积核遍历这16个特征图，进行相加融合。这个过程使用了 16 × 3 × 3 + 16 × 32 × 1 × 1 = 656 16 \times 3 \times 3 + 16 \times 32 \times 1 \times 1 = 656 16×3×3+16×32×1×1=656个参数，远少于4608个参数。
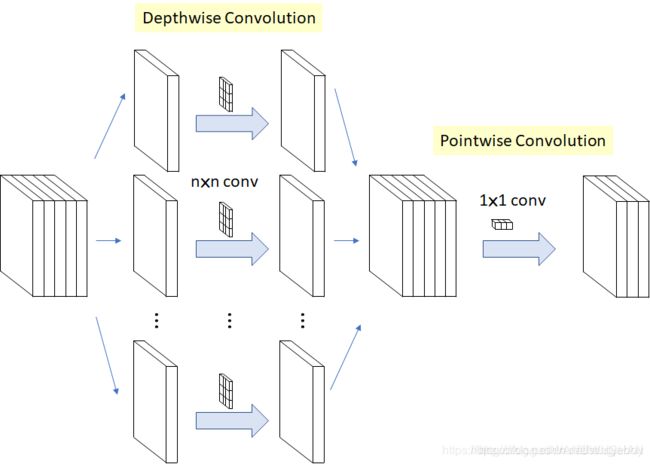
计算公式
- 传统卷积计算量
D K ∗ D K ∗ M ∗ N ∗ D F ∗ D F D_K * D_K * M * N * D_F * D_F DK∗DK∗M∗N∗DF∗DF - 深度可分离卷积计算量
- depthwise convolution计算量
D K ∗ D K ∗ M ∗ D F ∗ D F D_K * D_K * M * D_F * D_F DK∗DK∗M∗DF∗DF - pointwise convolution计算量
1 ∗ 1 ∗ M ∗ N ∗ D F ∗ D F 1 * 1 * M * N * D_F * D_F 1∗1∗M∗N∗DF∗DF - 整体计算量
D K ∗ D K ∗ M ∗ D F ∗ D F + 1 ∗ 1 ∗ M ∗ N ∗ D F ∗ D F D_K * D_K * M * D_F * D_F + 1 * 1 * M * N * D_F * D_F DK∗DK∗M∗DF∗DF+1∗1∗M∗N∗DF∗DF
- depthwise convolution计算量
- 深度可分离卷积与常规卷积计算量比值
D K ∗ D K ∗ M ∗ D F ∗ D F + 1 ∗ 1 ∗ M ∗ N ∗ D F ∗ D F D K ∗ D K ∗ M ∗ N ∗ D F ∗ D F = 1 N + 1 D K 2 \frac{D_K * D_K * M * D_F * D_F + 1 * 1 * M * N * D_F * D_F}{D_K * D_K * M * N * D_F * D_F}=\frac{1}{N} + \frac{1}{D^{2}_{K}} DK∗DK∗M∗N∗DF∗DFDK∗DK∗M∗DF∗DF+1∗1∗M∗N∗DF∗DF=N1+DK21
当channel数上百层时， 1 N \frac{1}{N} N1部分可以忽略，若 K = 3 K=3 K=3，即采用 3 × 3 3 \times 3 3×3卷积时，结果约为 1 8 ∼ 1 9 \frac{1}{8} \sim \frac{1}{9} 81∼91，即深度可分离卷积计算量会减少到常规卷积的 1 8 ∼ 1 9 \frac{1}{8} \sim \frac{1}{9} 81∼91。
深度可分离卷积的优点
- 神经可分离卷积与普通卷积相比，减少了所需要的参数。
- 深度可分离卷积将以往普通卷积操作同时考虑通道和区域变成先只考虑区域，在考虑通道，实现了通道和区域的分离。
- 深度可以分离卷积也有通道信息融合，它的过程分为两个部分：depthwise（逐层）+pointwise（逐像素）。前者负责卷积运算，后者使用 1 × 1 1 \times 1 1×1卷积核进行通道的像素融合。
分组卷积
概念
分组卷积（Group convolution）最早在AlexNet中出现，由于当时的硬件资源有限，训练AlexNet时卷积操作不能全部放在同一GPU处理，因此作者把feature maps分给多个GPU分别进行处理，最后把多个GPU的结果进行融合。
- 一般卷积操作
一般卷积会对输入数据的整体一起做卷积操作。
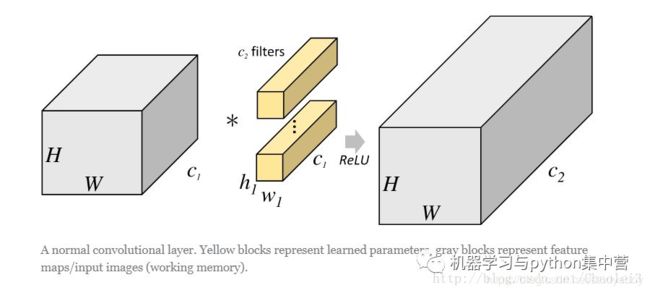
- 分组卷积
分组卷积将输入数据在深度（即通道上）进行了分组，即某几个通道编为一组，相应的卷积核也需要作出同样的改变，而卷积核大小不需要改变。每组的卷积核同它们对应组内的输入数据卷积，得到输出数据后，再用concatenate的方式组合起来。
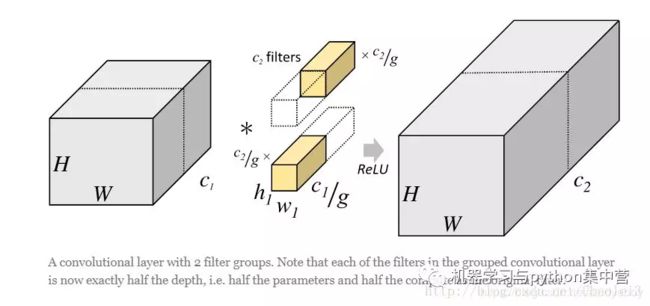
- Group conv本身就极大的减少了参数
比如当输入通道维256，输出通道维256，kernel size为 3 × 3 3 \times 3 3×3，不做group conv参数为 256 × 3 × 3 × 256 256 \times 3 \times 3 \times 256 256×3×3×256。实施分组卷积时，若group为8，每个group的input channel和output channel均为32，参数为 8 × 32 × 3 × 3 × 32 8 \times 32 \times 3 \times 3 \times 32 8×32×3×3×32，是原来的八分之一。而group conv最后每一组输出的feature maps应该是以concatenate的方式组合。Alex认为group conv的方式能够增加filter之间的对角相关性，而且能够减少训练参数，不容易过拟合，这类似于正则的效果。
可变形卷积
传统的卷积核一般是长方形或正方形，但MSRA提出了一个相当反直觉的见解，认为卷积核的形状可以是变化的，变形的卷积核能让让只看感兴趣的图像区域，这样识别出来的特征更佳。可变形的卷积核，可以看成是视觉领域的新视界。
可变形的卷积实现是基于标准的卷积核的，只不过在标准卷积核中每一个卷积核单元还附带两个位置偏移量（x,y）， x，y表示像素相对于中心像素的位置偏移，即现在每个像素的值是一个形如（value，x，y）的三元组，x，y为偏移量，但是具体的偏移量不是人为指定，虽然也可以这么做，具体的偏移量时多少，每一个像素的偏移是不一样的，让网络去学习这个x，y。
参考资料
- A guide to convolution arithmetic for deep learning
- conv_arithmetic
- 卷积，空洞卷积、可分离卷积
- 一文看懂普通卷积、转置卷积transposed convolution、空洞卷积dilated convolution以及depthwise separable convolution
- 一文了解各种卷积结构原理及优劣
- MobileNets:Efficient Convolutional Neural Networks for Mobile Vision Applications
- 对深度可分离卷积、分组卷积、空洞卷积的通俗理解(上篇)
- 对转置卷积、可变形卷积、通道加权卷积的通俗理解(下篇)
- Deformable Convolutional Networks