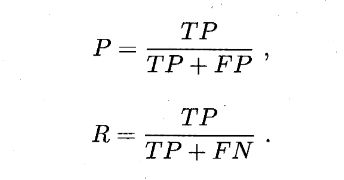机器学习笔记--PR曲线和ROC曲线
最近在看周志华老师的机器学习,本文主要是对PR图和ROC曲线的整理。
一、PR图
对于二分类问题,根据分类结果能形成“混淆矩阵”。
- 查准率P类似于,“检索出的信息中有多少比例是用户感兴趣的”;
- 查准率R类似于,“用户感兴趣的信息中有多少被检索出来了”;
一般来说,查准率和查全率是一对矛盾的度量,书上给出的“P-R图”比较平滑,现实中局部波动较大。
二、ROC曲线
ROC全称是“受试者工作特征”曲线,纵轴是“真正例率”TPR,横轴是“假正例率”FPR,两者同样基于混淆矩阵,定义如下:
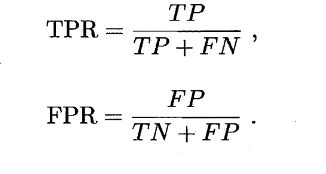
可以通过AUC(曲线下的面积)比较两个分类器的性能。
三、如何画PR图和ROC曲线
我们要清楚的是,分类器做预测,是不会直接输出类别符号,而是给出属于某个类别的概率值,比如说预测当前西瓜是好瓜的概率是80%。PR曲线和AOC曲线的画法是差不多的,根据分类器的预测结果从大到小对样例进行排序,逐个把样例加入正例进行预测,算出此时的P、R值。
为了方便,我直接代码实现了。代码如下:
#!/usr/bin/env python
# -*-coding:utf-8 -*-
'''
@File : test.py
@Time : 2020/03/11 20:27:25
@Author : Schiller Xu
@Version : 1.0
@Contact : [email protected]
@License : (C)Copyright 2020-2021, SchillerXu
@Desc : None
'''
import random
import numpy as np
import matplotlib.pyplot as pt
list_p=[]
list_r=[]
list_tp=[]
list_fp=[]
list_tpr=[]
list_fpr=[]
#正例数和反例数
number_p=25
number_n=25
#产生正反例和预测值,按照预测值从大到小排列
list_data=[[1,random.random()] for i in range(number_p)]
list_neg=[[-1,random.random()] for i in range(number_n)]
list_data.extend(list_neg)
list_data.sort(key=lambda x: x[1],reverse=True)
for i in list_data:
print(i)
if list_data[0][0]==-1:
list_fp.append(1)
list_tp.append(0)
else:
list_tp.append(1)
list_fp.append(0)
list_p.append(list_tp[0]/(list_tp[0]+list_fp[0]))
list_r.append(list_tp[0]/number_p)
list_tpr.append(list_tp[0]/number_p)
list_fpr.append(list_fp[0]/number_n)
for i in range(1,number_p+number_n):
if list_data[i][0]==1:
list_tp.append(list_tp[i-1]+1)
list_fp.append(list_fp[i-1])
else:
list_tp.append(list_tp[i-1])
list_fp.append(list_fp[i-1]+1)
list_p.append(list_tp[i]/(list_tp[i]+list_fp[i]))
list_r.append(list_tp[i]/number_p)
list_tpr.append(list_tp[i]/number_p)
list_fpr.append(list_fp[i]/number_n)
for i in range(number_p+number_n):
print("("+str(list_r[i])+','+str(list_p[i])+')')
x=np.array(list_r)
y=np.array(list_p)
tpr=np.array(list_tpr)
fpr=np.array(list_fpr)
#PR图蓝色表示
pt.plot(x, y,'b--o',label='PR')
#ROC绿色表示
pt.plot(fpr,tpr,'g--o',label='ROC')
pt.legend()
pt.xlim(0, 1)
pt.ylim(0, 1)
pt.title("PR and ROC curve")
pt.show()
其中一次的数据样本如下:
[1, 0.972465136805586]
[1, 0.9699186889290848]
[1, 0.9611558285258316]
[1, 0.9490100343890661]
[1, 0.945494922623268]
[-1, 0.9298404375249634]
[-1, 0.9253050908724593]
[1, 0.9179792320057252]
[1, 0.9029249172614586]
[-1, 0.8985088203989411]
[-1, 0.8920543556575127]
[-1, 0.8750351381751852]
[-1, 0.8504740280725512]
[1, 0.8374708361478499]
[-1, 0.8253450779514403]
[-1, 0.8244418984124263]
[1, 0.8181527020041762]
[-1, 0.752244236642972]
[1, 0.7460862224109783]
[1, 0.7432261084515641]
[1, 0.7409454088712828]
[-1, 0.7371362748455107]
[-1, 0.6822955149067242]
[1, 0.5985675419027885]
[-1, 0.5715525471916322]
[1, 0.5531563190065774]
[1, 0.5485301371231199]
[-1, 0.5175250115700692]
[-1, 0.5090063218073044]
[1, 0.5010686374084308]
[-1, 0.482313862965455]
[1, 0.44738013073917726]
[1, 0.43372870862894697]
[-1, 0.4261195587899538]
[1, 0.3776112552826205]
[-1, 0.28961604761188553]
[-1, 0.27955075928742346]
[1, 0.27829042206703614]
[1, 0.2782864067012276]
[-1, 0.27185534894732455]
[-1, 0.23773265429953483]
[-1, 0.22413723937794816]
[1, 0.2119534778887895]
[1, 0.18704185168412202]
[-1, 0.17552218100533823]
[-1, 0.14101947435168005]
[-1, 0.09985538173639386]
[-1, 0.051404226082772286]
[1, 0.025664213506509492]
[1, 0.01205253729664213]
1代表现实是正例,-1代表现实是反例,后面是预测值。我们可以按照书上的方法手动推几个:
分类的阈值首先定为0.972465136805586,只有大于等于阈值的为预测为正例,其他的都是反例,那么TP=1,FP=0,P=1,R=0.04,TPR=0.04,FPR=0;
阈值如果定为0.9699186889290848,TP=2,FP=0,P=1,R=0.08,TPR=0.08,FPR=0
……
……
最后PR图和ROC曲线如下:
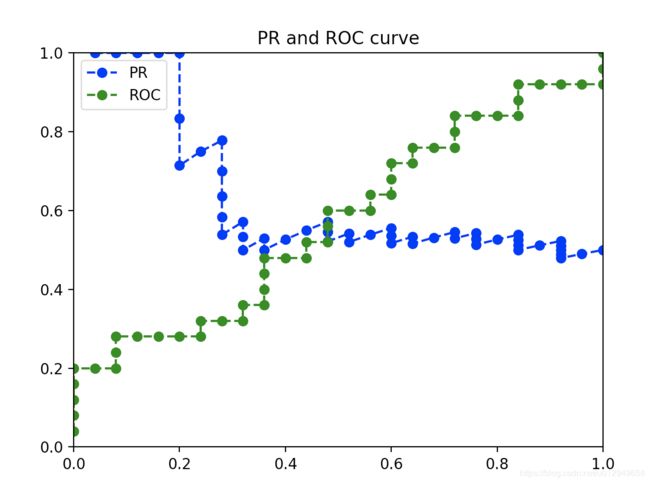
和书上平滑的曲线差别较大,而且PR曲线受样本数据分布影响较大。
四、参考资料
文中部分机器学习的图侵删;
PR曲线和F1、ROC曲线和AUC
Matplotlib.pyplot 常用方法