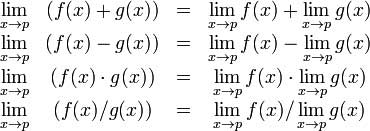了解Matlab
概述
MATLAB(矩阵实验室)是数字计算,可视化和编程的第四代高级编程语言和交互式环境。MATLAB是由MathWorks开发的。
它允许矩阵操纵,绘制功能和数据; 实现算法; 创建用户界面; 与其他语言编写的程序(包括C语言,C++,Java和FORTRAN)进行交互; 分析数据; 开发算法; 并创建模型和应用程序。
它有许多内置命令和数学函数,可以帮助您进行数学计算,生成图形和执行数值方法。
MATLAB计算数学
MATLAB用于计算数学的各个方面,以下是最常用的常用数学计算方法 -
- 处理矩阵和数组
- 2D和3D绘图和图形
- 线性代数
- 代数方程
- 非线性函数
- 统计
- 数据分析
- 微积分和微分方程
- 数值计算
- 积分
- 变换
- 曲线拟合
各种其他特殊功能
MATLAB特点
以下是MATLAB的基本特性 -
- 它是数字计算,可视化和应用程序开发的高级语言。
- 它还为迭代探索,设计和解决问题提供了一个交互式环境。
- 它为线性代数,统计学,傅里叶分析,滤波,优化,数值积分和求解常微分方程提供了广泛的数学函数库。
- 它提供内置的图形,用于可视化数据和工具,用于创建自定义绘图。
- MATLAB编程接口提供了开发工具,以提高代码质量的可维护性并最大限度提高性能。
- 它提供使用自定义图形界面构建应用程序的工具。
它提供了基于MATLAB的算法与外部应用程序和语言(如C语言,Java,.NET和Microsoft Excel)集成的功能。
MATLAB使用
MATLAB广泛应用于物理,化学,数学和所有工程流领域的科学与工程计算工具。 它用于一系列应用,包括 -
- 信号处理和通信
- 图像和视频处理
- 控制系统
- 测试和测量
- 计算财务
计算生物学
Matlab命令
管理会话的命令
MATLAB提供了各种用于管理会话的命令。下表提供了所有这些命令 -
| 命令 | 描述说明 |
|---|---|
| clc | 清除命令窗口 |
| clear | 从内存中删除变量 |
| exist | 检查文件或变量是否存在 |
| global | 声明变量为全局变量 |
| help | 搜索帮助主题 |
| lookfor | 搜索帮助关键字的条目。 |
| quit | 停止MATLAB |
| who | 列出当前变量 |
| whos | 列出当前变量(长显示详细信息) |
使用系统命令
MATLAB提供了各种有用的命令来处理系统,比如将工作区中的当前工作保存为文件,稍后加载文件。
它还为其他系统相关活动提供各种命令,如显示日期,列出目录中的文件,显示当前目录等。
下表显示了一些常用的系统相关命令 -
| 命令 | 描述说明 |
|---|---|
| cd | 更改当前目录(进入指定目录) |
| date | 显示当前日期 |
| delete | 删除文件 |
| diary | 打开/关闭日记文件记录 |
| dir | 列出当前目录下的所有文件 |
| load | 从文件加载工作区变量 |
| path | 显示搜索路径 |
| pwd | 显示当前目录 |
| save | 将工作空间变量保存在文件中 |
| type | 显示文件的内容 |
| what | 列出当前目录中的所有MATLAB文件 |
| wklread | 读取.wk1电子表格文件 |
输入和输出命令
MATLAB提供以下输入和输出相关命令 -
| 命令 | 描述说明 |
|---|---|
| disp | 显示数组或字符串的内容 |
| fscanf | 从文件读取格式化数据 |
| format | 控制屏幕显示格式 |
| fprintf | 对屏幕或文件执行格式化的写入 |
| input | 显示提示并等待输入 |
| ; | 禁止打印显示 |
fscanf和fprintf命令的行为类似于C语言中的scanf和printf函数。它们支持以下格式代码 -
| 命令 | 描述说明 |
|---|---|
| %s | 格式化为字符串 |
| %d | 格式化为字符串整数值 |
| %f | 格式化为浮点值 |
| %e | 格式化为科学记数法的浮点值 |
| %g | 格式最紧凑的形式:%f或%e。 |
| \n | 在输出字符串中插入一个换行 |
| \t | 在输出字符串中插入制表符 |
格式化(format)函数具有以下用于数字显示的形式 -
| 命令 | 描述说明 |
|---|---|
| format short | 4位十进制数(默认) |
| format long | 16位数字 |
| format short e | 5位数加上指数 |
| format long e | 16位加上指数 |
| format bank | 两位十进制数字 |
| format + | 正,负或零 |
| format rat | 有理近似 |
| format compact | 禁止一些换行符 |
| format loose | 重置为较不紧凑的显示模式 |
向量,矩阵和数组命令
下表显示了用于处理数组,矩阵和向量的各种命令 -
| 命令 | 描述说明 |
|---|---|
| cat | 连接数组 |
| find | 查找非零元素的索引 |
| length | 计算元素数量 |
| linspace | 创建规则间隔的向量 |
| logspace | 创建对数间隔向量 |
| max | 返回最大的元素 |
| min | 返回最小的元素 |
| prod | 产生的每列 |
| reshape | 改变大小 |
| size | 计算数组大小 |
| sort | 对每列进行排序 |
| sum | 对每列进行求和 |
| eye | 创建一个单位矩阵 |
| ones | 创建一个数组 |
| zeros | 创建一个零的数组 |
| cross | 计算矩阵交叉积 |
| dot | 计算矩阵点积 |
| det | 计算数组的行列式 |
| inv | 计算矩阵的倒数 |
| pinv | 计算矩阵的伪逆 |
| rank | 计算矩阵的秩 |
| rref | 计算简化行阶梯形式 |
| cell | 创建单元格数组 |
| celldisp | 显示单元格数组 |
| cellplot | 显示单元格阵列的图形表示 |
| num2cell | 将数组转换为单元格数组 |
| deal | 匹配输入和输出列表 |
| iscell | 识别单元格数组 |
绘图命令
MATLAB提供了许多用于绘制图形的命令。下表显示了一些常用的绘图命令 -
| 命令 | 描述说明 |
|---|---|
| axis | 设置轴限制 |
| fplot | 智能绘图功能 |
| grid | 显示网格线 |
| plot | 生成xy坐标图 |
| 打印或绘图到文件 | |
| title | 在文字的顶部放置文字 |
| xlabel | 将文本标签添加到x轴 |
| ylabel | 将文本标签添加到y轴 |
| axes | 创建轴对象 |
| close | 关闭当前坐标图 |
| close all | 关闭所有坐标图 |
| figure | 打开一个新的图形窗口 |
| gtext | 通过鼠标启用标签放置 |
| hold | 冻结当前坐标图 |
| legend | 通过鼠标图例位置 |
| refresh | 重新绘制当前图形窗口 |
| set | 指定诸如轴的对象的属性 |
| subplot | 在子窗口中创建图 |
| text | 在图开放置字符串 |
| bar | 创建条形图 |
| loglog | 创建日志记录图 |
| polar | 创建极坐标图 |
| semilogx | 创建半标记图(对数横坐标) |
| semilogy | 创建半标记图(对数纵坐标) |
| stairs | 创建梯形图 |
| stem | 创建茎图 |
Matlab .m脚本文件
到目前为止,我们都是使用MATLAB环境作为计算器。然而,MATLAB也是一种强大的编程语言,也是一个交互式的计算环境。
在前几章中,已经学习了如何从MATLAB命令提示符输入命令。MATLAB还允许将一系列命令写入文件,并将文件作为完整单元执行,如:编写函数并调用它。
M文件
MATLAB允许编写两种程序文件 -
- 脚本 -
脚本文件是以.m扩展名的程序文件。在这些文件中,可以编写一系列要一起执行的命令。脚本不接受输入,不返回任何输出。它们对工作空间中的数据进行操作。 - 函数 - 函数文件也是扩展名为.m的程序文件。函数可以接受输入和返回输出。内部变量是函数的局部变量。
使用MATLAB编辑器或任何其他文本编辑器来创建.m文件。 在本节中,我们将讨论脚本文件。 脚本文件包含多个连续的MATLAB命令行和函数调用。可以通过在命令行中键入其名称来运行脚本。
创建和运行脚本文件
要创建脚本文件,需要使用文本编辑器。可以通过两种方式打开MATLAB编辑器:
- 使用命令提示符
- 使用IDE
如果使用命令提示符,请在命令提示符下键入edit并回车,这将打开编辑器。可以直接键入edit,然后直接输入文件名(扩展名为.m)
edit
%或者%
edit newfile.m在命令行中也可以创建文件夹,如:创建一个名为progs的文件夹。在命令提示符下键入以下命令(>>):
mkdir progs % create directory progs under default directory
chdir progs % changing the current directory to progs
edit prog1.m % creating an m file named prog1.m或者,如果使用IDE,请选择“新建” ->“脚本”。 这也打开编辑器并创建一个名为Untitled的文件。在输入代码后命名并保存文件。
在编辑器中键入以下代码 -
NoOfStudents = 6000;
TeachingStaff = 150;
NonTeachingStaff = 20;
Total = NoOfStudents + TeachingStaff + NonTeachingStaff;
disp(Total);创建并保存文件后,可以通过两种方式运行:
- 单击编辑器窗口上的“运行”按钮
- 只需在命令提示符下键入文件名(无扩展名)即可:>> prog1
命令窗口提示符显示结果 -
示例
创建脚本文件(sdemo.m),并键入以下代码 -
a = 5; b = 7;
c = a + b
d = c + sin(b)
e = 5 * d
f = exp(-d)当上述代码被编译和执行时,它产生以下结果 -
Trial>> sdemo
c =
12
d =
12.6570
e =
63.2849
f =
3.1852e-06
Trial>>Matlab数据类型
MATLAB不需要任何类型声明或维度语句。当MATLAB遇到新的变量名称时,它将创建变量并分配适当的内存空间。
如果变量已经存在,则MATLAB将使用新内容替换原始内容,并在必要时分配新的存储空间。
例如,
total = 136;上述语句创建一个名为total的1x1矩阵,并将值136存储在其中。
MATLAB数据类型
MATLAB提供15种基本数据类型。每种数据类型存储矩阵或数组形式的数据。矩阵或数组的最小值是0到0,并且是可以到任何大小的矩阵或数组。
下表显示了MATLAB中最常用的数据类型 -
| 数据类型 | 描述 |
|---|---|
| int8 | 8位有符号整数 |
| uint8 | 8位无符号整数 |
| int16 | 16位有符号整数 |
| uint16 | 16位无符号整数 |
| int32 | 32位有符号整数 |
| uint32 | 32位无符号整数 |
| int64 | 64位有符号整数 |
| uint64 | 64位无符号整数 |
| single | 单精度数值数据 |
| double | 双精度数值数据 |
| logical | 逻辑值为1或0,分别代表true和false |
| char | 字符数据(字符串作为字符向量存储) |
| 单元格阵列 | 索引单元阵列,每个都能够存储不同维数和数据类型的数组 |
| 结构体 | C型结构,每个结构具有能够存储不同维数和数据类型的数组的命名字段 |
| 函数处理 | 指向一个函数的指针 |
| 用户类 | 用户定义的类构造的对象 |
| Java类 | 从Java类构造的对象 |
示例
使用以下代码创建脚本文件(datatype1.m) -
str = 'Hello World!'
n = 2345
d = double(n)
un = uint32(789.50)
rn = 5678.92347
c = int32(rn)当上述代码被编译和执行时,它产生以下结果 -
Trial>> datatype1
str =
'Hello World!'
n =
2345
d =
2345
un =
uint32
790
rn =
5.6789e+03
c =
int32
5679数据类型转换
MATLAB提供了各种用于将一种数据类型转换为另一种数据类型的函数。 下表显示了数据类型转换函数 -
| 函数 | 描述说明 |
|---|---|
| char | 转换为字符数组(字符串) |
| int2str | 将整数数据转换为字符串 |
| mat2str | 将矩阵转换为字符串 |
| num2str | 将数字转换为字符串 |
| str2double | 将字符串转换为双精度值 |
| str2num | 将字符串转换为数字 |
| native2unicode | 将数字字节转换为Unicode字符 |
| unicode2native | 将Unicode字符转换为数字字节 |
| base2dec | 将基数N字符串转换为十进制数 |
| bin2dec | 将二进制数字串转换为十进制数 |
| dec2base | 将十进制转换为字符串中的N数字 |
| dec2bin | 将十进制转换为字符串中的二进制数 |
| dec2hex | 将十进制转换为十六进制数字 |
| hex2dec | 将十六进制数字字符串转换为十进制数 |
| hex2num | 将十六进制数字字符串转换为双精度数字 |
| num2hex | 将单数转换为IEEE十六进制字符串 |
| cell2mat | 将单元格数组转换为数组 |
| cell2struct | 将单元格数组转换为结构数组 |
| cellstr | 从字符数组创建字符串数组 |
| mat2cell | 将数组转换为具有潜在不同大小的单元格的单元阵列 |
| num2cell | 将数组转换为具有一致大小的单元格的单元阵列 |
| struct2cell | 将结构转换为单元格数组 |
数据类型确定
MATLAB提供了用于识别变量数据类型的各种函数。
下表提供了确定变量数据类型的函数 -
| 函数 | 描述说明 |
|---|---|
| is | 检测状态 |
| isa | 确定输入是否是指定类的对象 |
| iscell | 确定输入是单元格数组 |
| iscellstr | 确定输入是字符串的单元格数组 |
| ischar | 确定项目是否是字符数组 |
| isfield | 确定输入是否是结构数组字段 |
| isfloat | 确定输入是否为浮点数组 |
| ishghandle | 确定是否用于处理图形对象句柄 |
| isinteger | 确定输入是否为整数数组 |
| isjava | 确定输入是否为Java对象 |
| islogical | 确定输入是否为逻辑数组 |
| isnumeric | 确定输入是否是数字数组 |
| isobject | 确定输入是否为MATLAB对象 |
| isreal | 检查输入是否为实数数组 |
| isscalar | 确定输入是否为标量 |
| isstr | 确定输入是否是字符数组 |
| isstruct | 确定输入是否是结构数组 |
| isvector | 确定输入是否为向量 |
| class | 确定对象的类 |
| validateattributes | 检查数组的有效性 |
| whos | 在工作区中列出变量,其大小和类型 |
示例
使用以下代码创建脚本文件 -
x = 3
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
isnumeric(x)
x = 23.54
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
isnumeric(x)
x = [1 2 3]
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
x = 'Hello'
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
isnumeric(x)
MATLAB运行文件后,产生以下结果 -
x = 3
ans = 0
ans = 1
ans = 1
ans = 1
ans = 1
x = 1177/50
ans = 0
ans = 1
ans = 1
ans = 1
ans = 1
x =
1 2 3
ans = 0
ans = 1
ans = 1
ans = 0
x = Hello
ans = 0
ans = 0
ans = 1
ans = 0
ans = 0Matlab运算符
运算符是一个符号,它告诉编译器执行特定的数学或逻辑操作。 MATLAB主要用于整个矩阵和阵列的操作。因此,MATLAB中的运算符既可用于标量数据也可用于非标量数据。MATLAB允许以下类型的基本操作 -
- 算术运算符
- 关系运算符
- 逻辑运算符
- 按位运算符
- 集合运算符
下面我们来一个一个地学习。
算术运算符
MATLAB允许两种不同类型的算术运算 -
- 矩阵算术运算
- 数组算术运算
矩阵算术运算与线性代数中定义的相同。在一维和多维数组中,逐个元素执行数组运算。
矩阵运算符和数组运算符由句点符号(.)区分。 然而,由于对于矩阵和阵列的加减运算是相同的,因此对于这两种情况,运算符相同。下表简要说明了算术运算符 -
算术运算符示例代码
关系运算符
关系运算符也可以用于标量和非标量数据。数组的关系运算符在两个数组之间执行逐个元素的比较,并返回相同大小的逻辑数组,如果为真,则元素设置为逻辑1(true),如果为假,则元素设置为逻辑0(false)。
下表显示了MATLAB中可用的关系运算符:
关系运算符示例代码
| 操作符 | 说明描述 |
|---|---|
| < | 小于 |
| <= | 小于或等于 |
| > | 大于 |
= |
大于或等于 |
| == | 等于 |
| ~= | 不等于 |
逻辑运算符
MATLAB提供两种类型的逻辑运算符和函数:
- 逐元素 - 这些运算符对逻辑阵列的相应元素进行操作。
- 短路 - 这些运算符在标量和逻辑表达式上运行。
元素逻辑运算符在逻辑数组上运行逐个元素。符号&,|和〜是逻辑数组运算符AND,OR和NOT。
短路逻辑运算符允许逻辑运算短路。符号&&和||是逻辑短路运算符AND和OR。
逻辑运算符示例代码
位运算
按位运算符对位执行,并执行逐位运算。&,|和^的真值表如下 -
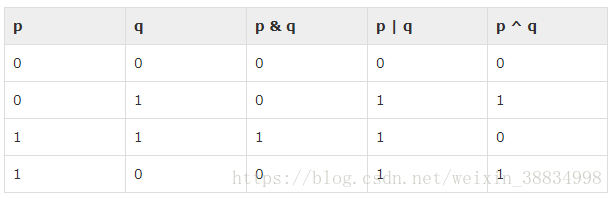
假设A = 60和B = 13; 现在以二进制格式,它们将如下所示:
A = 0011 1100
B = 0000 1101
-----------------
A&B = 0000 1100
A|B = 0011 1101
A^B = 0011 0001
~A = 1100 0011MATLAB提供了诸如“按位与”和“按位或”以及“按位非”操作,移位操作等位操作的各种功能。
下表显示了常用的按位操作:
按位操作示例
| 方法 | 目的 |
|---|---|
| bitand(a, b) | 整数a和b的位与AND操作 |
| bitcmp(a) | a的比特补码 |
| bitget(a,pos) | 在整数数组a中,获取指定的位置pos位字节 |
| bitor(a, b) | 整数a和b的逐位OR操作 |
| bitset(a, pos) | 设置在指定pos处的位字节 |
| bitshift(a, k) | 返回向左移位k字节,相当于乘以2^k。 k的负值对应于向右移位或除以2^ k 并舍入到最接近的整数到负无穷大。任何溢出位都被截断。 |
| bitxor(a, b) | 整数a和b的逐字节位XOR操作 |
| swapbytes | 交换字节排序 |
集合操作
MATLAB为集合操作提供了各种功能,如联合,交集和集合成员的测试等。
下表显示了一些常用的集合操作 -
| 函数 | 描述 |
|---|---|
| intersect(A,B) | 设置两个阵列的交集; 也就是返回A和B共同的值。返回的值按排序顺序排列。 |
| intersect(A,B,’rows’) | 将A的每一行和B的每一行视为单个实体,并返回A和B两者共同的行。返回矩阵的行按排序顺序排列。 |
| ismember(A,B) | 返回与A相同大小的数组,其中包含1(true),其中A的元素位于B中。其他地方返回0(false)。 |
| ismember(A,B,’rows’) | 将A的每行和B的每一行视为单个实体,并返回一个包含1(true)的向量,其中矩阵A的行也是B行。其他返回0(false)。 |
| issorted(A) | 如果A的元素按排序顺序返回逻辑1(真),否则返回逻辑0(假)。输入A可以是一个向量,也可以是N-by-1或1-by-N的字符串数组。 如果A和sort(A)的输出相等,则认为A被排序。 |
| issorted(A, ‘rows’) | 如果二维矩阵A的行按排序顺序返回逻辑1(真),否则返回逻辑0(假)。 如果A和排序(A)的输出相等,则认为矩阵A被排序。 |
| setdiff(A,B) | 设置两个数组的差异; 返回A中不在B中的值。返回的数组中的值按排序顺序排列。 |
| setdiff(A,B,’rows’) | 将A的每一行和B的每一行视为单个实体,并从不在B中的A返回行。返回的矩阵的行按排序顺序排列。’rows’选项不支持单元格数组。 |
| setxor | 设置两个数组的异或 |
| union | 设置两个数组的并集 |
| unique | 使数组中的值唯一 |
Matlab决策
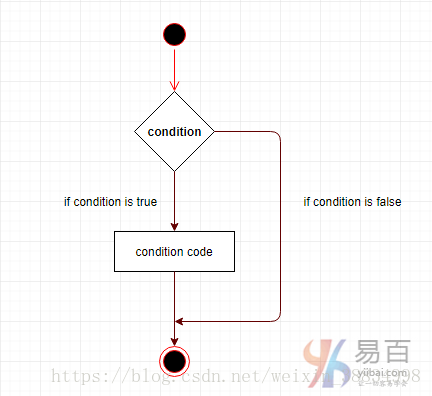
决策结构要求程序员应指定要由程序评估计算或测试的一个或多个条件,以及条件确定为真时要执行的语句或语句,如果条件被确定为假时,可选地如果执行其他语句。
MATLAB提供以下类型的决策语句。点击以下链接来查看它们的详细说明 -
| 语句 | 描述 |
|---|---|
| if…end语句 | if … end语句包含一个布尔表达式,后跟一个或多个语句。 |
| if…else…end语句 | if语句可以跟随一个可选的else语句,当布尔表达式为false时,else语句块将执行。 |
| if…elseif…elseif…else…end语句 | if语句后面可以有一个(或多个)可选elseif …和一个else语句,这对于测试各种条件非常有用。 |
| 嵌套if语句 | 可以在一个if或elseif语句中使用另一个if或elseif语句。 |
| switch语句 | switch语句用来测试一个变量与值列表的相等性。 |
| 嵌套switch语句 | 可以在一个switch语句中使用一个switch语句。 |
Matlab循环
当需要执行一段代码多次时可以使用循环语句。 一般来说,语句是按顺序执行的。首先执行函数中的第一个语句,然后执行第二个语句,依此类推。
编程语言提供了允许更复杂的执行路径的各种控制结构。
循环语句允许多次执行一个语句或一组语句,以下是大多数编程语言中循环语句的一般形式 -
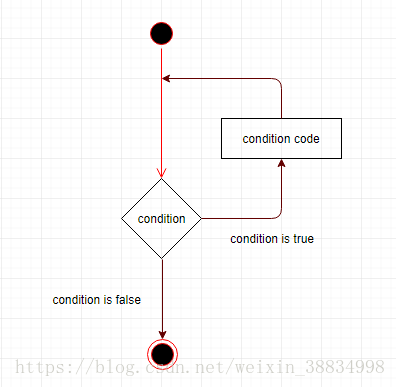
MATLAB提供以下类型的循环来处理循环需求。点击以下链接来查看它们的详细说明和使用 -
| 循环类型 | 描述 |
|---|---|
| while循环 | 在给定条件为真时,重复一个语句或一组语句。它在执行循环体之前测试状态。 |
| for循环 | 多次执行一系列语句,并缩写管理循环变量的代码。 |
| 嵌套循环 | 在任何循环中使用另外一个或多个循环。 |
循环控制语句
循环控制语句从其正常顺序更改执行。当执行离开范围时,在该范围内创建的所有自动对象都将被销毁。
MATLAB支持以下控制语句。点击以下链接来查看它们的详细说明和使用 -
| 控制语句 | 描述 |
|---|---|
| break语句 | 终止循环语句,并将执行转移到循环之后的语句。 |
| continue语句 | 导致循环跳过主体的剩余部分,并在重申之前立即重新测试其状态。 |
Matlab向量
向量是数字的一维数组。在MATLAB中,允许创建两种类型的向量 -
- 行向量
- 列向量
行向量
行向量是通过用方括号中的元素集合来创建的,使用空格或逗号分隔元素。
r = [1 18 19 21 41]MATLAB将执行上述语句并返回以下结果 -
Trial>> r = [1 18 19 21 41]
r =
1 18 19 21 41列向量
列向量是通过用方括号中的元素集合来创建的,分号用于分隔元素。
c = [17; 28; 39; 60; 81]MATLAB将执行上述语句,返回以下结果 -
Trial>> c = [17; 28; 39; 60; 81]
c =
17
28
39
60
81引用向量的元素
可以通过多种方式来引用一个或多个向量的元素。向量v的第i个分量叫作v(i)。 例如 -
v = [ 1; 2; 3; 4; 5; 6]; % creating a column vector of 6 elements
v(3)MATLAB执行上述语句,返回以下结果 -
Trial>> v = [ 1; 2; 3; 4; 5; 6]; % creating a column vector of 6 elements
v(3)
ans =
3引用带冒号的向量(如v(:))时,将列出向量的所有组件。
v = [ 1; 2; 3; 4; 5; 6]; % creating a column vector of 6 elements
v(:)MATLAB执行上述语句,返回以下结果 -
Trial>> v = [ 1; 2; 3; 4; 5; 6]; % creating a column vector of 6 elements
v(:)
ans =
1
2
3
4
5
6MATLAB可从向量中选择一系列元素。
例如,创建一个9个元素的行向量rv,然后通过rv(3:7)引用3到7元素,然后引用来向一个新创建的sub_rv向量赋值。如下代码所示 -
rv = [1 2 3 4 5 6 7 8 9];
sub_rv = rv(3:7)
MATLAB
MATLAB将执行上述语句并返回以下结果 -
Trial>> rv = [1 2 3 4 5 6 7 8 9];
sub_rv = rv(3:7)
sub_rv =
3 4 5 6 7
向量运算
在本节中,让我们讨论和学习以下向量的操作 -
- 向量的加减
- 向量的标量乘法
- 转置向量
- 附加向量
- 向量的幅值大小
- 向量点积
- 具有均匀间隔元素的向量
Matlab矩阵
矩阵是数字的二维数组。
在MATLAB中,可以通过在每行中输入元素来创建一个矩形,以逗号或空格分隔数字,并使用分号标记每一行的结尾。
例如,创建一个4×5矩阵a -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]MATLAB将执行上述语句并返回以下结果 -
Trial>> a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]
a =
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8引用矩阵中的元素
要引用矩阵mx的第m行和第n列中的元素,可以这样书写 -
mx(m, n);例如,要引用矩阵a的第2行和第5列中的元素,如上一节所述,可以这样书写 -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(2,5)MATLAB执行上述语句并返回以下结果 -
Trial>> a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(2,5)
ans =
6要引用第m列中的所有元素,可以使用A(:,m)。
假设要从矩阵a的第4行元素来创建列向量v:
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
v = a(:,4)MATLAB执行上述语句并返回以下结果 -
Trial>> a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
v = a(:,4)
v =
4
5
6
7还可以选择第m至第n列中的元素,代码如下 -
a(:,m:n)下面是创建一个更小的矩阵,从第二和第三列的元素 -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(:, 2:3)MATLAB执行上述语句并返回以下结果 -
Trial>> a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(:, 2:3)
ans =
2 3
3 4
4 5
5 6以同样的方式,可以创建一个矩阵的子部分的子矩阵。
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(:, 2:3)MATLAB执行上述语句并返回以下结果 -
Trial>> a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(:, 2:3)
ans =
2 3
3 4
4 5
5 6以同样的方式,可以创建一个矩阵的子部分的子矩阵。
例如,要创建一个子矩阵sa,其包含以下内容的内部子部分:
3 4 5
4 5 6参考以下实例代码 -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
sa = a(2:3,2:4)MATLAB执行上述语句,返回以下结果 -
sa =
3 4 5
4 5 6删除矩阵中的一行或一列
通过向该行或列分配一组空的方括号[]来删除矩阵的整个行或列。[]表示一个空数组。
例如,删除第四行 -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a( 4 , : ) = []MATLAB执行上述语句,返回以下结果 -
a =
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7接下来,删除第五列 -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(: , 5)=[]MATLAB执行上述语句,返回以下结果 -
a =
1 2 3 4
2 3 4 5
3 4 5 6
4 5 6 7例子
在这个例子中,首先创建一个3x3的矩阵m,然后复制该矩阵的第二行和第三行两次来创建一个4x3的矩阵。
使用以下代码创建脚本文件 -
a = [ 1 2 3 ; 4 5 6; 7 8 9];
new_mat = a([2,3,2,3],:)运行文件时,它产生以下结果 -
new_mat =
4 5 6
7 8 9
4 5 6
7 8 9矩阵运算
在本节中,让我们讨论和学习下面一些常用的矩阵运算 -
- 矩阵的加法和减法
a = [ 1 2 3 ; 4 5 6; 7 8 9];
b = [ 7 5 6 ; 2 0 8; 5 7 1];
c = a + b
d = a - b
c =
8 7 9
6 5 14
12 15 10
d =
-6 -3 -3
2 5 -2
2 1 8- 矩阵除法
a = [ 1 2 3 ; 4 5 6; 7 8 9];
b = [ 7 5 6 ; 2 0 8; 5 7 1];
c = a / b
d = a \ b
c =
-0.52542 0.68644 0.66102
-0.42373 0.94068 1.01695
-0.32203 1.19492 1.37288
d =
-3.27778 -1.05556 -4.86111
-0.11111 0.11111 -0.27778
3.05556 1.27778 4.30556- 矩阵的标量运算
a = [ 10 12 23 ; 14 8 6; 27 8 9];
b = 2;
c = a + b
d = a - b
e = a * b
f = a / b
c =
12 14 25
16 10 8
29 10 11
d =
8 10 21
12 6 4
25 6 7
e =
20 24 46
28 16 12
54 16 18
f =
5.0000 6.0000 11.5000
7.0000 4.0000 3.0000
13.5000 4.0000 4.5000- 矩阵的转置
a = [ 10 12 23 ; 14 8 6; 27 8 9]
b = a'
a =
10 12 23
14 8 6
27 8 9
b =
10 14 27
12 8 8
23 6 9- 矩阵连接
Trial>> a = [ 10 12 23 ; 14 8 6; 27 8 9]
b = [ 12 31 45 ; 8 0 -9; 45 2 11]
c = [a, b]
d = [a; b]
a =
10 12 23
14 8 6
27 8 9
b =
12 31 45
8 0 -9
45 2 11
c =
10 12 23 12 31 45
14 8 6 8 0 -9
27 8 9 45 2 11
d =
10 12 23
14 8 6
27 8 9
12 31 45
8 0 -9
45 2 11
- 矩阵乘法
考虑有两个矩阵A和B,如果A是m×n矩阵,并且B是n×p矩阵,则它们可以相乘以产生m×n矩阵C。仅当A中的列数n等于B中行n数量时,才能进行矩阵乘法 。
在矩阵乘法中,第一矩阵中的行的元素与第二矩阵中的相应列相乘。
所得到的矩阵C中的(i,j)位置中的每个元素是第一矩阵的第i行中的元素的乘积与第二矩阵的第j列中的相应元素的和。
a =
1 2 3
2 3 4
1 2 5
b =
2 1 3
5 0 -2
2 3 -1
prod =
18 10 -4
27 14 -4
22 16 -6- 矩阵的行列式
Trial>> a = [ 1 2 3; 2 3 4; 1 2 5]
det(a)
a =
1 2 3
2 3 4
1 2 5
ans =
-2- 矩阵的逆转
矩阵A的倒数由A-1表示,使得以下关系成立 -
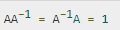
矩阵的倒数并不总是存在。如果矩阵的行列式为零,则不存在逆矩阵,矩阵是单数的。
a = [ 1 2 3; 2 3 4; 1 2 5]
inv(a)
a =
1 2 3
2 3 4
1 2 5
ans =
-3.5000 2.0000 0.5000
3.0000 -1.0000 -1.0000
-0.5000 0 0.5000Matlab数组
MATLAB中所有数据类型的所有变量都是多维数组。向量是一维数组,矩阵是二维数组。
我们前面已经讨论和学习过向量和矩阵。 在本章中,将讨论和学习多维数组。 然而,在此之前,让我们先学习一些特殊类型的数组。
MATLAB中的特殊数组
在本节中,我们将讨论学习一些创建一些特殊数组的函数。对于这些函数,单个参数创建一个正方形数组,双参数创建矩形数组。
zeros()函数是用来创建一个全零的数组 -
例如 -
zeros(5)执行上面示例代码,得到以下结果 -
Trial>> zeros(5)
ans =
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0ones()函数创建一个所有元素为1的数组 -
例如 -
ones(4,3)执行上面示例代码,得到以下结果 -
Trial>> ones(4,3)
ans =
1 1 1
1 1 1
1 1 1
1 1 1eye()函数创建一个单位矩阵。
例如 -
eye(4)执行上面示例代码,得到以下结果 -
Trial>> eye(4)
ans =
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1rand()函数在(0,1) - 上创建均匀分布的随机数的数组 -
例如 -
rand(3, 5)执行上面示例代码,得到以下结果 -
Trial>> rand(3, 5)
ans =
0.8147 0.9134 0.2785 0.9649 0.9572
0.9058 0.6324 0.5469 0.1576 0.4854
0.1270 0.0975 0.9575 0.9706 0.8003魔方
魔方是一个平方,它产生相同的和,它的元素被逐行,逐列或者对角线地添加时。
magic()函数创建一个魔术方阵。这需要一个参数,指定正方形的大小。 参数必须是大于或等于3的标量。
magic(4)
执行上面示例代码,得到以下结果 -
Trial>> magic(4)
ans =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1多维数组
具有二维以上的数组在MATLAB中被称为多维数组。MATLAB中的多维数组是正常二维矩阵的扩展。
通常要生成一个多维数组,首先创建一个二维数组然后再扩展它。
例如,让我们创建一个二维数组a。
a = [7 9 5; 6 1 9; 4 3 2]执行上面示例代码,得到以下结果 -
Trial>> a = [7 9 5; 6 1 9; 4 3 2]
a =
7 9 5
6 1 9
4 3 2数组a是3×3数组; 可以通过提供以下值来添加第三维:
a(:, :, 2)= [ 1 2 3; 4 5 6; 7 8 9]执行上面示例代码,得到以下结果 -
a =
ans(:,:,1) =
0 0 0
0 0 0
0 0 0
ans(:,:,2) =
1 2 3
4 5 6
7 8 9还可以使用ones(),zeros()或rand()函数来创建多维数组。
例如,
b = rand(4,3,2)执行上面示例代码,得到以下结果 -
Trial>> b = rand(4,3,2)
b(:,:,1) =
0.1419 0.9595 0.9340
0.4218 0.6557 0.6787
0.9157 0.0357 0.7577
0.7922 0.8491 0.7431
b(:,:,2) =
0.3922 0.0318 0.8235
0.6555 0.2769 0.6948
0.1712 0.0462 0.3171
0.7060 0.0971 0.9502也可以使用cat()函数来构建多维数组。它沿着指定的维度连接数组列表 -
cat()函数的语法是 -
B = cat(dim, A1, A2...)其中,
B是创建的新阵列
A1,A2,…是要连接的数组
dim是连接数组的大小
例子
创建脚本文件并在其中键入以下代码 -
a = [9 8 7; 6 5 4; 3 2 1];
b = [1 2 3; 4 5 6; 7 8 9];
c = cat(3, a, b, [ 2 3 1; 4 7 8; 3 9 0])执行上面示例代码,得到以下结果 -
c(:,:,1) =
9 8 7
6 5 4
3 2 1
c(:,:,2) =
1 2 3
4 5 6
7 8 9
c(:,:,3) =
2 3 1
4 7 8
3 9 0数组函数
MATLAB提供以下函数来对数组内容进行排序,旋转,排列,重新成形或移位。
| 函数 | 描述 |
|---|---|
| length | 向量的大小或数组的长度 |
| ndims | 数组的维数 |
| numel | 数组的元素数量 |
| size | 数组的维度 |
| iscolumn | 确定输入是否为列向量 |
| isempty | 确定数组是否为空 |
| ismatrix | 确定输入是否为矩阵 |
| isrow | 确定输入是否为行向量 |
| isscalar | 确定输入是否为标量 |
| isvector | 确定输入是否为向量 |
| blkdiag | 从输入参数构造块对角矩阵 |
| circshift | 循环移位 |
| ctranspose | 复共轭转置 |
| diag | 矩阵对角矩阵和对角线 |
| flipdim | 沿着指定的尺寸翻转数组 |
| fliplr | 从左到右翻转矩阵 |
| flipud | 向下翻转矩阵 |
| ipermute | 反转N-D阵列的置换维度 |
| permute | 重新排列N-D数组的维度 |
| repmat | 复制和平铺数组 |
| reshape | 重塑数组 |
| rot90 | 旋转矩阵90度 |
| shiftdim | 移动维度 |
| issorted | 确定设置元素是否按排序顺序 |
| sort | 按升序或降序排列数组元素 |
| sortrows | 按升序排列行 |
| squeeze | 删除单例维度 |
| transpose | 转置 |
| vectorize | 向量化表达式 |
例子
以下的例子说明了上面提到的一些函数。
长度,尺寸和元素数量:
创建脚本文件并键入以下代码 -
x = [7.1, 3.4, 7.2, 28/4, 3.6, 17, 9.4, 8.9];
length(x) % length of x vector
y = rand(3, 4, 5, 2);
ndims(y) % no of dimensions in array y
s = ['Zara', 'Nuha', 'Shamim', 'Riz', 'Shadab'];
numel(s) % no of elements in s运行文件时,显示以下结果 -
ans = 8
ans = 4
ans = 23数组元素的循环移位
创建脚本文件并在其中键入以下代码 -
a = [1 2 3; 4 5 6; 7 8 9] % the original array a
b = circshift(a,1) % circular shift first dimension values down by 1.
c = circshift(a,[1 -1]) % circular shift first dimension values % down by 1
% and second dimension values to the left % by 1.运行文件文件时,显示以下结果 -
a =
1 2 3
4 5 6
7 8 9
b =
7 8 9
1 2 3
4 5 6
c =
8 9 7
2 3 1
5 6 4排序数组
创建脚本文件并在其中键入以下代码 -
v = [ 23 45 12 9 5 0 19 17] % horizontal vector
sort(v) % sorting v
m = [2 6 4; 5 3 9; 2 0 1] % two dimensional array
sort(m, 1) % sorting m along the row
sort(m, 2) % sorting m along the column运行文件文件时,显示以下结果 -
v =
23 45 12 9 5 0 19 17
ans =
0 5 9 12 17 19 23 45
m =
2 6 4
5 3 9
2 0 1
ans =
2 0 1
2 3 4
5 6 9
ans =
2 4 6
3 5 9
0 1 2单元阵列
单元格阵列是索引单元的数组,其中每个单元格可以存储不同维度和数据类型的数组。
单元格函数用于创建单元格数组。单元格函数的语法是 -
C = cell(dim)
C = cell(dim1,...,dimN)
D = cell(obj)其中,
- C是单元阵列;
- dim是一个整数或整数向量,它指定单元格数组C的维数;
- dim1,…,dimN是指定C大小的标量整数;
- obj是以下之一:
- Java数组或对象
- 类型为System.String或System.Object的.NET数组
示例
创建脚本文件并在其中键入以下代码 -
c = cell(2, 5);
c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5}运行文件时,得到以下结果 -
c =
{
[1,1] = Red
[2,1] = 1
[1,2] = Blue
[2,2] = 2
[1,3] = Green
[2,3] = 3
[1,4] = Yellow
[2,4] = 4
[1,5] = White
[2,5] = 5
}访问单元格数组数据
有两种方法来引用单元格数组的元素 -
- 将第一个括号()中的索引包围,以引用单元格集
- 将大括号{}中的索引括起来,以引用单个单元格内的数据
当将索引包围在第一个括号中时,它指的是这组单元格。
括号中的单元格数组索引是指单元格集。
例如:
c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5};
c(1:2,1:2)运行文件时,得到以下结果 -
ans =
{
[1,1] = Red
[2,1] = 1
[1,2] = Blue
[2,2] = 2
}还可以通过用花括号索引来访问单元格的内容。
例如 -
c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5};
c{1, 2:4}运行文件时,得到以下结果 -
ans = Blue
ans = Green
ans = YellowMatlab冒号符号
冒号(:)是MATLAB中最有用的操作符之一。它用于创建向量,下标数组,并为迭代指定。
如果要创建一个包含从1到10的整数的行向量,则书写为 -
1:10MATLAB执行语句并返回一个包含整数的行向量,从1到10 -
ans =
1 2 3 4 5 6 7 8 9 10如果要指定一个增量值,例如 -
100: -5: 50MATLAB执行语句并返回以下结果 -
ans =
100 95 90 85 80 75 70 65 60 55 50再来看看一个例子 -
0:pi/8:piMATLAB执行语句并返回以下结果 -
ans =
Columns 1 through 7
0 0.3927 0.7854 1.1781 1.5708 1.9635 2.3562
Columns 8 through 9
2.7489 3.1416可以使用冒号运算符创建索引向量,以选择数组的行,列或元素。
下表描述了其用于此目的(假设有一个矩阵A) -
| 格式 | 目的 |
|---|---|
| A(:,j) | 是A的第j列 |
| A(i,:) | 是A的第i行 |
| A(:,:) | 是等效的二维数组。对于矩阵,这与A相同。 |
| A(j:k) | 是A(j), A(j+1),…,A(k) |
| A(:,j:k) | 是A(:,j), A(:,j+1),…,A(:,k) |
| A(:,:,k) | 是三维数组A的第k页 |
| A(i,j,k,:) | 是四维数组A中的向量。向量包括A(i,j,k,1),A(i,j,k,2),A(i,j,k,3)等。 |
| A(:) | 是A的所有要素,被视为单列。在赋值语句的左侧,A(:)填充A,从之前保留其形状。在这种情况下,右侧必须包含与A相同数量的元素。 |
示例
创建脚本文件并在其中键入以下代码 -
A = [1 2 3 4; 4 5 6 7; 7 8 9 10]
A(:,2) % second column of A
A(:,2:3) % second and third column of A
A(2:3,2:3) % second and third rows and second and third columns运行文件时,会显示以下结果 -
A =
1 2 3 4
4 5 6 7
7 8 9 10
ans =
2
5
8
ans =
2 3
5 6
8 9
ans =
5 6
8 9Matlab数字
MATLAB支持包括有符号和无符号整数以及单精度和双精度浮点数的各种数字类型。 默认情况下,MATLAB将所有数值存储为双精度浮点数。
可以选择将任何数字或数组的数字存储为整数或单精度数字。
所有数字类型都支持基本的数组运算和数学运算。
转换为各种数值数据类型
MATLAB提供以下函数来将数值转换为各种数字数据类型 -
| 函数 | 描述说明 |
|---|---|
| double | 转换为双精度数 |
| single | 转换为单精度数 |
| int8 | 转换为8位有符号整数 |
| int16 | 转换为16位有符号整数 |
| int32 | 转换为32位有符号整数 |
| int64 | 转换为64位有符号整数 |
| uint8 | 转换为8位无符号整数 |
| uint16 | 转换为16位无符号整数 |
| uint32 | 转换为32位无符号整数 |
| uint64 | 转换为64位无符号整数 |
示例
创建脚本文件并键入以下代码 -
x = single([5.32 3.47 6.28]) .* 7.5
x = double([5.32 3.47 6.28]) .* 7.5
x = int8([5.32 3.47 6.28]) .* 7.5
x = int16([5.32 3.47 6.28]) .* 7.5
x = int32([5.32 3.47 6.28]) .* 7.5
x = int64([5.32 3.47 6.28]) .* 7.5执行上面示例代码,得到以下结果 -
x =
39.900 26.025 47.100
x =
39.900 26.025 47.100
x =
38 23 45
x =
38 23 45
x =
38 23 45
x =
38 23 45示例
让我们再来扩展上面的例子。 创建脚本文件并键入以下代码 -
x = int32([5.32 3.47 6.28]) .* 7.5
x = int64([5.32 3.47 6.28]) .* 7.5
x = num2cell(x)执行上面示例代码,得到以下结果 -
Trial>> x = int32([5.32 3.47 6.28]) .* 7.5
x = int64([5.32 3.47 6.28]) .* 7.5
x = num2cell(x)
x =
1×3 int32 行向量
38 23 45
x =
1×3 int64 行向量
38 23 45
x =
1×3 cell 数组
{[38]} {[23]} {[45]}最小和最大的整数
intmax()和intmin()函数返回可以用所有类型的整数表示的最大值和最小值。
这两个函数将整数数据类型作为参数,例如int_max(int8)或intmin(int64),并返回可以使用整数数据类型表示的最大值和最小值。
示例
以下示例说明如何获取最小和最大的整数值。 创建脚本文件并在其中写下面的代码 -
% displaying the smallest and largest signed integer data
str = 'The range for int8 is:\n\t%d to %d ';
sprintf(str, intmin('int8'), intmax('int8'))
str = 'The range for int16 is:\n\t%d to %d ';
sprintf(str, intmin('int16'), intmax('int16'))
str = 'The range for int32 is:\n\t%d to %d ';
sprintf(str, intmin('int32'), intmax('int32'))
str = 'The range for int64 is:\n\t%d to %d ';
sprintf(str, intmin('int64'), intmax('int64'))
% displaying the smallest and largest unsigned integer data
str = 'The range for uint8 is:\n\t%d to %d ';
sprintf(str, intmin('uint8'), intmax('uint8'))
str = 'The range for uint16 is:\n\t%d to %d ';
sprintf(str, intmin('uint16'), intmax('uint16'))
str = 'The range for uint32 is:\n\t%d to %d ';
sprintf(str, intmin('uint32'), intmax('uint32'))
str = 'The range for uint64 is:\n\t%d to %d ';
sprintf(str, intmin('uint64'), intmax('uint64'))执行上面示例代码,得到以下结果 -
ans =
'The range for int8 is:
-128 to 127 '
ans =
'The range for int16 is:
-32768 to 32767 '
ans =
'The range for int32 is:
-2147483648 to 2147483647 '
ans =
'The range for int64 is:
-9223372036854775808 to 9223372036854775807 '
ans =
'The range for uint8 is:
0 to 255 '
ans =
'The range for uint16 is:
0 to 65535 '
ans =
'The range for uint32 is:
0 to 4294967295 '
ans =
'The range for uint64 is:
0 to 1.844674e+19 '最小和最大的浮点数
realmax()和realmin()函数返回可以用浮点数表示的最大值和最小值。
当使用参数’single’调用这两个函数时,返回使用单精度数据类型表示的最大值和最小值,当使用参数’double’调用时,返回可以表示的最大值和最小值的双精度数据类型。
示例
以下示例说明如何获取最小和最大的浮点数。 创建脚本文件并在其中写下面的代码 -
% displaying the smallest and largest single-precision
% floating point number
str = 'The range for single is:\n\t%g to %g and\n\t %g to %g';
sprintf(str, -realmax('single'), -realmin('single'), ...
realmin('single'), realmax('single'))
% displaying the smallest and largest double-precision
% floating point number
str = 'The range for double is:\n\t%g to %g and\n\t %g to %g';
sprintf(str, -realmax('double'), -realmin('double'), ...
realmin('double'), realmax('double'))执行上面示例代码,得到以下结果 -
ans =
'The range for single is:
-3.40282e+38 to -1.17549e-38 and
1.17549e-38 to 3.40282e+38'
ans =
'The range for double is:
-1.79769e+308 to -2.22507e-308 and
2.22507e-308 to 1.79769e+308'Matlab字符串
在MATLAB中创建一个字符串非常简单。 事实上,在前面的示例中我们已经使用了很多次。 例如,在命令提示符下键入以下内容:
my_string = ‘Yiibai Yiibai’
MATLAB执行上述语句并返回以下结果 -
Trial>> my_string = 'Yiibai Yiibai'
my_string =
'Yiibai Yiibai'MATLAB将所有变量视为数组,并将字符串视为字符数组。使用whos命令来检查上面创建的变量 -
Trial>> whos
Name Size Bytes Class Attributes
ans 1x92 184 char
my_string 1x16 32 char
x 1x3 360 cell有趣的是,可以使用uint8或uint16等数字转换函数将字符串中的字符转换为数字代码。 char函数将整数向量转换回到字符 -
示例
创建脚本文件并在其中键入以下代码 -
my_string = 'Yiibai''s Tutorial';
str_ascii = uint8(my_string) % 8-bit ascii values
str_back_to_char= char(str_ascii)
str_16bit = uint16(my_string) % 16-bit ascii values
str_back_to_char = char(str_16bit)执行上面示例代码,得到以下结果 -
str_ascii =
1×17 uint8 行向量
1 至 15 列
89 105 105 98 97 105 39 115 32 84 117 116 111 114 105
16 至 17 列
97 108
str_back_to_char =
'Yiibai's Tutorial'
str_16bit =
1×17 uint16 行向量
1 至 15 列
89 105 105 98 97 105 39 115 32 84 117 116 111 114 105
16 至 17 列
97 108
str_back_to_char =
'Yiibai's Tutorial'矩形字符数组
到目前为止,我们讨论的字符串是一维字符数组; 然而,我们需要存储更多维度的数据。在程序中存储更多的维度文本数据。这是通过创建矩形字符数组来实现的。
创建矩形字符阵列的最简单的方式是根据需要垂直或水平连接两个或更多个一维字符数组。
通过以下任一方式垂直组合字符串 -
使用MATLAB连接运算符[]并用分号(;)分隔每一行。 请注意,在这种方法中,每行必须包含相同数量的字符。对于不同长度的字符串,应该根据需要填充空格字符。
使用char函数。如果字符串的长度不同,则char将较短的字符串填充到尾部空白处,以使每行具有相同的字符数。
示例
创建脚本文件并在其中键入以下代码 -
doc_profile = ['Bara Tli '; ...
'Sr. Surgeon '; ...
'R N Tagore Cardiology Research Center']
doc_profile = char('Bara Tli', 'Sr. Surgeon', ...
'RN Tagore Cardiology Research Center')运行文件时,会显示以下结果 -
Trial>> doc_profile = ['Bara Tli '; ...
'Sr. Surgeon '; ...
'R N Tagore Cardiology Research Center']
doc_profile = char('Bara Tli', 'Sr. Surgeon', ...
'RN Tagore Cardiology Research Center')
doc_profile =
3×37 char 数组
'Bara Tli '
'Sr. Surgeon '
'R N Tagore Cardiology Research Center'
doc_profile =
3×36 char 数组
'Bara Tli '
'Sr. Surgeon '
'RN Tagore Cardiology Research Center'可以通过以下任一方式水平组合字符串 -
- 使用MATLAB连接运算符 - []并用逗号(;)或空格分隔输入字符串。该方法保留输入数组中的任何尾随空格。
- 使用字符串连接函数 - strcat。 此方法会删除输入中的尾随空格。
示例
创建脚本文件并在其中键入以下代码 -
name = 'Myra Yli ';
position = 'Sr. Surgeon ';
worksAt = 'R N Tagore Cardiology Research Center';
profile = [name ', ' position ', ' worksAt]
profile = strcat(name, ', ', position, ', ', worksAt)执行上面示例代码,得到以下结果 -
Trial>> name = 'Myra Yli ';
position = 'Sr. Surgeon ';
worksAt = 'R N Tagore Cardiology Research Center';
profile = [name ', ' position ', ' worksAt]
profile = strcat(name, ', ', position, ', ', worksAt)
profile =
'Myra Yli , Sr. Surgeon , R N Tagore Cardiology Research Center'
profile =
'Myra Yli,Sr. Surgeon,R N Tagore Cardiology Research Center'将字符串组合成单元格数组
从前面的学习中,很明显,组合不同长度的字符串可能会很痛苦,因为数组中的所有字符串都必须具有相同的长度。在字符串的末尾使用了空格,使其长度相等。
然而,组合字符串的更有效的方法是将生成的数组转换为单元格数组。
MATLAB单元格数组可以在数组中保存不同大小和类型的数据。单元格数组提供了一种更灵活的方法来存储不同长度的字符串。
cellstr函数将字符数组转换为字符串的单元格数组。
示例
创建脚本文件并在其中键入以下代码 -
name = 'Myra Tli ';
position = 'St. Sargeon ';
worksAt = 'R N Tagore Cardiology Research Center';
profile = char(name, position, worksAt);
profile = cellstr(profile);
disp(profile)执行上面示例代码,得到以下结果 -
Trial>> name = 'Myra Tli ';
position = 'St. Sargeon ';
worksAt = 'R N Tagore Cardiology Research Center';
profile = char(name, position, worksAt);
profile = cellstr(profile);
disp(profile)
'Myra Tli'
'St. Sargeon'
'R N Tagore Cardiology Research Center'MATLAB中的字符串函数
MATLAB提供了许多字符串函数来创建,组合,解析,比较和操作字符串。
下表简要介绍了MATLAB中的字符串函数。
用于存储字符数组中的文本,组合字符数组等的函数 -
| 函数 | 描述 |
|---|---|
| blanks | 创建空白字符串 |
| cellstr | 从字符数组创建字符串数组 |
| char | 转换为字符数组(字符串) |
| iscellstr | 确定输入是字符串的单元格数组 |
| ischar | 确定项目是否是字符数组 |
| sprintf | 将数据格式化为字符串 |
| strcat | 水平连接字符串 |
| strjoin | 将单元格中的字符串连接到单个字符串中 |
识别字符串部分,查找和替换子串的函数 -
| 函数 | 描述 |
|---|---|
| ischar | 确定项目是否是字符数组 |
| isletter | 数组元素是否为字母 |
| isspace | 数组元素是空格 |
| isstrprop | 确定字符串是否是指定的类别 |
| sscanf | 从字符串读取格式化数据 |
| strfind | 在另一个字符串中查找一个字符串 |
| strrep | 查找并替换子串 |
| strsplit | 在指定的分隔符处拆分字符串 |
| strtok | 字符串的选定部分 |
| validatestring | 检查文本字符串的有效性 |
| symvar | 确定表达式中的符号变量 |
| regexp | 匹配正则表达式(区分大小写) |
| regexpi | 匹配正则表达式(不区分大小写) |
| regexprep | 用正则表达式替换字符串 |
| regexptranslate | 用正则表达式替换字符串 |
字符串比较的函数 -
| 函数 | 描述 |
|---|---|
| strcmp | 比较字符串(区分大小写) |
| strcmpi | 比较字符串(不区分大小写) |
| strncmp | 比较字符串的前n个字符(区分大小写) |
| strncmpi | 比较字符串的前n个字符(不区分大小写) |
将字符串更改为大写或小写,创建或删除空格的函数 -
| 函数 | 描述 |
|---|---|
| deblank | 从字符串末尾剥去尾随空格 |
| strtrim | 从字符串中删除前导和尾随的空格 |
| lower | 将字符串转换为小写 |
| upper | 将字符串转换为大写字母 |
| strjust | 对齐字符数组 |
例子
以下示例说明了一些上述字符串函数 -
格式化字符串
创建脚本文件并在其中键入以下代码 -
A = pi*1000*ones(1,5);
sprintf(' %f \n %.2f \n %+.2f \n %12.2f \n %012.2f \n', A)执行上面示例代码,得到以下结果 -
ans = 3141.592654
3141.59
+3141.59
3141.59
000003141.59字符串连接
创建脚本文件并在其中键入以下代码 -
%cell array of strings
str_array = {'red','blue','green', 'yellow', 'orange'};
% Join strings in cell array into single string
str1 = strjoin(str_array, "-")
str2 = strjoin(str_array, ",")执行上面示例代码,得到以下结果 -
str1 = red-blue-green-yellow-orange
str2 = red,blue,green,yellow,orange查找和替换字符串
创建脚本文件并在其中键入以下代码 -
students = {'Bara Ali', 'Neha Bhatnagar', ...
'Nonica Malik', 'Madhu Gautam', ...
'Nadhu Sharma', 'Bhawna Sharma',...
'Muha Ali', 'Reva Dutta', ...
'Tunaina Ali', 'Sofia Kabir'};
% The strrep function searches and replaces sub-string.
new_student = strrep(students(8), 'Reva', 'Poulomi')
% Display first names
first_names = strtok(students)执行上面示例代码,得到以下结果 -
Trial>> students = {'Bara Ali', 'Neha Bhatnagar', ...
'Nonica Malik', 'Madhu Gautam', ...
'Nadhu Sharma', 'Bhawna Sharma',...
'Muha Ali', 'Reva Dutta', ...
'Tunaina Ali', 'Sofia Kabir'};
% The strrep function searches and replaces sub-string.
new_student = strrep(students(8), 'Reva', 'Poulomi')
% Display first names
first_names = strtok(students)
new_student =
1×1 cell 数组
{'Poulomi Dutta'}
first_names =
1×10 cell 数组
1 至 7 列
{'Bara'} {'Neha'} {'Nonica'} {'Madhu'} {'Nadhu'} {'Bhawna'} {'Muha'}
8 至 10 列
{'Reva'} {'Tunaina'} {'Sofia'}比较字符串
创建脚本文件并在其中键入以下代码 -
str1 = 'This is test'
str2 = 'This is text'
if (strcmp(str1, str2))
sprintf('%s and %s are equal', str1, str2)
else
sprintf('%s and %s are not equal', str1, str2)
end执行上面示例代码,得到以下结果 -
str1 = This is test
str2 = This is text
ans = This is test and This is text are not equalMatlab函数
一个函数是一组在一起执行任务的语句。 在MATLAB中,函数在单独的文件中定义。文件的名称和函数的名称应该是一样的。
函数在自己的工作空间内的变量上运行,这个变量也称为本地工作空间,与在MATLAB命令提示符下访问的工作区(称为基本工作区)不同。
函数可以接受多个输入参数,并可能返回多个输出参数。
函数语句的语法是 -
function [out1,out2, ..., outN] = myfun(in1,in2,in3, ..., inN)示例
以下名称为mymax的函数应写入名称为mymax.m的文件中。它需要五个数字作为参数,并返回参数数字值的最大值。
创建名为mymax.m的函数文件,从左上角菜单中点击新建->函数,并在其中键入以下代码 -
function max = mymax(n1, n2, n3, n4, n5)
% This function calculates the maximum of the
% five numbers given as input
max = n1;
if(n2 > max)
max = n2;
end
if(n3 > max)
max = n3;
end
if(n4 > max)
max = n4;
end
if(n5 > max)
max = n5;
end上面示例代码中,函数的第一行以关键字function开头。它给出了函数的名称和参数的顺序。在这个例子中,mymax函数有五个输入参数和一个输出参数。
函数语句之后的注释行提供了帮助文本。当键入时,这些行被打印 -
Trial>> help mymax
This function calculates the maximum of the
five numbers given as input现在,我们来调用这个函数 -
mymax(11,22,35,81,198)执行上面代码,得到以下结果 -
Trial>> mymax(11,22,35,81,198)
ans =
198匿名函数
匿名函数就像传统编程语言中的内联函数,在单个MATLAB语句中定义。 它由单个MATLAB表达式和任意数量的输入和输出参数组成。
可以在MATLAB命令行或函数或脚本中定义一个匿名函数。
这样就可以创建简单的函数,而无需为它们创建一个文件。
从表达式创建匿名函数的语法是 -
f = @(arglist)expression示例
在这个例子中,编写一个名为power的匿名函数,它将使用两个数字作为输入,并将第一个数字返回到第二个数字的幂值。
创建脚本文件并在其中键入以下代码 -
power = @(x, n) x.^n;
result1 = power(7, 3)
result2 = power(49, 0.5)
result3 = power(10, -10)
result4 = power (4.5, 1.5)当运行该文件,得到以下结果 -
result1 = 343
result2 = 7
result3 = 1.0000e-10
result4 = 9.5459主函数和次函数
必须在文件中定义除了匿名函数以外的其它任何函数。每个函数文件包含主要出现的必需的主函数,以及主函数之后的任意数量的可选子函数。
可以从命令行或其他函数的文件外部调用主函数,但不能从命令行或函数文件外的其他函数调用子函数。
子函数仅对函数文件中的主函数和其他子函数可见。
示例
下面编写一个名为quadratic的函数来计算二次方程的根。该函数需要三个输入参数:二次系数,线性系数和常数项。计算并会返回根。
函数文件quadratic.m将包含主函数quadratic和次函数和子函数disc,它计算判别式。
创建一个函数文件quadratic.m并在其中键入以下代码 -
function [x1,x2] = quadratic(a,b,c)
%this function returns the roots of
% a quadratic equation.
% It takes 3 input arguments
% which are the co-efficients of x2, x and the
%constant term
% It returns the roots
d = disc(a,b,c);
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end % end of quadratic
function dis = disc(a,b,c)
%function calculates the discriminant
dis = sqrt(b^2 - 4*a*c);
end % end of sub-function可以从命令提示符调用上述函数 -
Trial>> quadratic(2,4,-4)
ans =
0.7321嵌套函数
可以在一个函数的主体内定义另一个函数。这样的函数被称为嵌套函数。嵌套函数包含任何其他函数的部分或全部组件。
嵌套函数在另一个函数的范围内定义,并且它们共享对包含函数的工作空间的访问。
嵌套函数遵循以下语法 -
function x = A(p1, p2)
...
B(p2)
function y = B(p3)
...
end
...
end示例
下面来重写quadratic函数,从上一个例子来看,然而这次disc函数将是一个嵌套函数。
创建一个函数文件quadratic2.m并在其中键入以下代码 -
function [x1,x2] = quadratic2(a,b,c)
function disc % nested function
d = sqrt(b^2 - 4*a*c);
end % end of function disc
disc;
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end % end of function quadratic2在命令行窗口中调用quadratic2.m函数,得到以下结果 -
Trial>> quadratic2(2,4,-4)
ans =
0.7321
私有函数
私有函数是仅在有限的其他函数组中可见的主函数。如果不想公开函数的实现,则可以将其创建为私有函数。
私有函数处在在专用名称为私有的子文件夹中。
它们只对父文件夹中的函数可见。
示例
下面来重写二次函数。这一次,计算判别式的disc函数将是私有函数。
在工作目录中创建一个名为private的子文件夹(F:\worksp\matlab\private)。存储以下函数在文件disc.m中 -
function dis = disc(a,b,c)
%function calculates the discriminant
dis = sqrt(b^2 - 4*a*c);
end % end of sub-function在工作目录中创建一个函数quadratic3.m(对应目录为:F:\worksp\matlab),并在其中键入以下代码:
function [x1,x2] = quadratic3(a,b,c)
%this function returns the roots of
% a quadratic equation.
% It takes 3 input arguments
% which are the co-efficient of x2, x and the
%constant term
% It returns the roots
d = disc(a,b,c);
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end % end of quadratic3在Matlab命令行中,调用以上定义的函数 -
Trial>> quadratic3(2,4,-4)
ans =
0.7321全局变量
全局变量可由多个函数共享。 为此,需要在所有函数中声明变量为全局变量。
如果要从基本工作区访问该变量,则在命令行中声明该变量。
全局声明必须在函数实际使用变量之前进行。 将大写字母用于全局变量的名称是一个很好的做法,以区别于其他变量。
示例
下面创建一个名为average.m的函数文件,并在其中键入以下代码 -
function avg = average(nums)
global TOTAL
avg = sum(nums)/TOTAL;
end创建脚本文件并在其中键入以下代码 -
global TOTAL;
TOTAL = 10;
n = [34, 45, 25, 45, 33, 19, 40, 34, 38, 42];
av = average(n)执行上面示例代码,得到以下结果 -
Trial>> global TOTAL;
TOTAL = 10;
n = [36, 45, 35, 45, 33, 29, 50, 41, 58, 47];
av = average(n)
av =
41.9000Matlab数据导入
在MATLAB中导入数据意味着从外部文件加载数据。importdata函数允许加载不同格式的各种数据文件。它有以下五种形式 -
| 序号 | 函数 | 描述 |
|---|---|---|
| 1 | A = importdata(filename) | 从文件filename中将数据加载到数组A中。 |
| 2 | A = importdata(‘-pastespecial’) | 从系统剪贴板而不是从文件加载数据。 |
| 3 | A = importdata(_, delimiterIn) | 解析delimiterIn作为在ASCII文件,文件名或剪贴板数据中的列分隔符。可以使用delimiterIn与上述语法中的任何输入参数。 |
| 4 | A = importdata(_, delimiterIn, headerlinesIn) | 从ASCII文件,文件名或剪贴板加载数据,从行头标题In + 1开始读取数字数据。 |
| 5 | [A, delimiterOut, headerlinesOut] = importdata(_) | 返回在delimiterOut中检测到的输入ASCII文件的分隔符字符,并使用前面语法中的任何输入参数检测headerlinesOut中检测到的标题行数。 |
默认情况下,Octave不支持importdata()函数,因此必须搜索并安装此软件包,以使以下示例与Octave安装配合使用。
示例 - 1
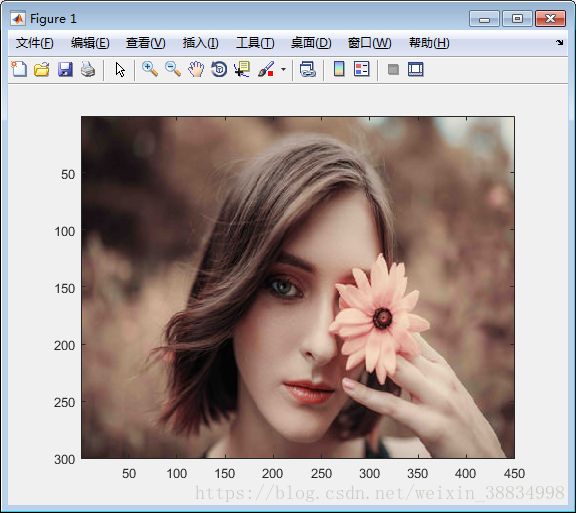
下面加载并显示一个图像文件。 创建脚本文件并在其中键入以下代码:
filename = 'photo1.jpg';
A = importdata(filename);
image(A);运行文件时,MATLAB显示图像文件。但是,必须将其存储在当前工作目录(F:\worksp\matlab)中。
示例 - 2
在这个例子中,导入一个文本文件并使用指定分隔符和列标题。下面用列标题创建一个空格分隔的ASCII文件,名称为weeklydata.txt。
文本文件weeklydata.txt的内容如下 -
周一 周二 周三 周四 周五 周六 周日
95.01 76.21 61.54 40.57 55.79 70.28 81.53
73.11 45.65 79.19 93.55 75.29 69.87 74.68
60.68 41.85 92.18 91.69 81.32 90.38 74.51
48.60 82.14 73.82 41.03 0.99 67.22 93.18
89.13 44.47 57.63 89.36 13.89 19.88 46.60创建脚本文件并在其中键入以下代码 -
Trial>> filename = 'weeklydata.txt';
delimiterIn = ' ';
headerlinesIn = 1;
A = importdata(filename,delimiterIn,headerlinesIn);
% View data
for k = [1:7]
disp(A.colheaders{1, k})
disp(A.data(:, k))
disp(' ')
end
周一
95.0100
73.1100
60.6800
48.6000
89.1300
周二
76.2100
45.6500
41.8500
82.1400
44.4700
周三
61.5400
79.1900
92.1800
73.8200
57.6300
周四
40.5700
93.5500
91.6900
41.0300
89.3600
周五
55.7900
75.2900
81.3200
0.9900
13.8900
周六
70.2800
69.8700
90.3800
67.2200
19.8800
周日
81.5300
74.6800
74.5100
93.1800
46.6000示例 - 3
在这个例子中,从剪贴板中导入数据。
将以下行复制到剪贴板 -
Matlab is simple,I like it.创建脚本文件并键入以下代码 -
A = importdata('-pastespecial')执行上面示例代码,得到以下结果 -
Trial>> A = importdata('-pastespecial')
A =
1×1 cell 数组
{'Matlab is simple,I like it.'}低级文件I/O
importdata函数是一个高级函数。 MATLAB中的低级文件I/O函数允许对文件读取或写入数据控制。但是,这些函数需要更多关于文件的详细信息才能有效地工作。
MATLAB为字节或字符级别的读写操作提供以下函数 -
| 函数 | 描述 |
|---|---|
| fclose | 关闭一个或所有打开的文件 |
| feof | 测试文件结尾 |
| ferror | 有关文件I/O错误的信息 |
| fgetl | 从文件读取行,删除换行符 |
| fgets | 从文件读取行,保留换行符 |
| fopen | 打开文件,或获取有关打开文件的信息 |
| fprintf | 将数据写入文本文件 |
| fread | 从二进制文件读取数据 |
| frewind | 将文件位置指示器移动到打开文件的开头 |
| fscanf | 从文本文件读取数据 |
| fseek | 移动到文件中的指定位置 |
| ftell | 在打开文件中的位置 |
| fwrite | 将数据写入二进制文件 |
导入具有低级别I/O的文本数据文件
MATLAB提供以下函数,用于低级导入文本数据文件 -
- fscanf函数读取文本或ASCII文件中的格式化数据。
- fgetl和fgets函数一次读取文件的一行,换行符分隔每行。
读取函数以字节或位级别读取数据流。
示例
假设有一个文本数据文件myfile.txt保存在工作目录中。此文件存放三个月的降雨资料: 2012年6月,7月和8月降雨量。
myfile.txt中的数据在五个地方包含重复的时间,月份和降雨量测量。标题数据存储月数M; 所以有M个集合测量值。
文件内容看起来如下 -
Rainfall Data
Months: June, July, August
M=3
12:00:00
June-2012
17.21 28.52 39.78 16.55 23.67
19.15 0.35 17.57 NaN 12.01
17.92 28.49 17.40 17.06 11.09
9.59 9.33 NaN 0.31 0.23
10.46 13.17 NaN 14.89 19.33
20.97 19.50 17.65 14.45 14.00
18.23 10.34 17.95 16.46 19.34
09:10:02
July-2012
12.76 16.94 14.38 11.86 16.89
20.46 23.17 NaN 24.89 19.33
30.97 49.50 47.65 24.45 34.00
18.23 30.34 27.95 16.46 19.34
30.46 33.17 NaN 34.89 29.33
30.97 49.50 47.65 24.45 34.00
28.67 30.34 27.95 36.46 29.34
15:03:40
August-2012
17.09 16.55 19.59 17.25 19.22
17.54 11.45 13.48 22.55 24.01
NaN 21.19 25.85 25.05 27.21
26.79 24.98 12.23 16.99 18.67
17.54 11.45 13.48 22.55 24.01
NaN 21.19 25.85 25.05 27.21
26.79 24.98 12.23 16.99 18.67从此文件导入数据并显示此数据。请按照以下步骤 -
- 使用fopen函数打开文件并获取文件标识符。
- 使用格式说明符描述文件中的数据,例如字符串的%s,整数%d或浮点数%f。
- 要跳过文件中的文字,请将其包含在格式说明中。要跳过数据字段,请在说明符中使用星号(*)。例如,要读取头文件并返回M的单个值,可以书写为:
M = fscanf(fid, '%*s %*s\n%*s %*s %*s %*s\nM=%d\n\n', 1);- 默认情况下,fscanf会根据格式描述读取数据,直到找不到数据的匹配,或到达文件的末尾。这里使用for循环读取3组数据,每次读取7行和5列。
- 将在工作空间中创建一个名为mydata的结构来存储从文件读取的数据。这个结构有三个字段 - 时间,月份和雨天数组。
创建脚本文件(readraindata.m)并在其中键入以下代码 -
filename = 'myfile.txt';
rows = 7;
cols = 5;
% open the file
fid = fopen(filename);
% read the file headers, find M (number of months)
M = fscanf(fid, '%*s %*s\n%*s %*s %*s %*s\nM=%d\n\n', 1);
% read each set of measurements
for n = 1:M
mydata(n).time = fscanf(fid, '%s', 1);
mydata(n).month = fscanf(fid, '%s', 1);
% fscanf fills the array in column order,
% so transpose the results
mydata(n).raindata = ...
fscanf(fid, '%f', [rows, cols]);
end
for n = 1:M
disp(mydata(n).time), disp(mydata(n).month)
disp(mydata(n).raindata)
end
% close the file
fclose(fid);执行上面示例代码,得到以下结果 -
Trial>> readraindata
12:00:00
June-2012
17.2100 17.5700 11.0900 13.1700 14.4500
28.5200 NaN 9.5900 NaN 14.0000
39.7800 12.0100 9.3300 14.8900 18.2300
16.5500 17.9200 NaN 19.3300 10.3400
23.6700 28.4900 0.3100 20.9700 17.9500
19.1500 17.4000 0.2300 19.5000 16.4600
0.3500 17.0600 10.4600 17.6500 19.3400
09:10:02
July-2012
12.7600 NaN 34.0000 33.1700 24.4500
16.9400 24.8900 18.2300 NaN 34.0000
14.3800 19.3300 30.3400 34.8900 28.6700
11.8600 30.9700 27.9500 29.3300 30.3400
16.8900 49.5000 16.4600 30.9700 27.9500
20.4600 47.6500 19.3400 49.5000 36.4600
23.1700 24.4500 30.4600 47.6500 29.3400
15:03:40
August-2012
17.0900 13.4800 27.2100 11.4500 25.0500
16.5500 22.5500 26.7900 13.4800 27.2100
19.5900 24.0100 24.9800 22.5500 26.7900
17.2500 NaN 12.2300 24.0100 24.9800
19.2200 21.1900 16.9900 NaN 12.2300
17.5400 25.8500 18.6700 21.1900 16.9900
11.4500 25.0500 17.5400 25.8500 18.6700Matlab数据导出
MATLAB中的数据导出(或输出)可以理解为写入文件。 MATLAB允许在其他应用程序中使用读取ASCII文件的数据。 为此,MATLAB提供了几个数据导出选项。
可以创建以下类型的文件:
来自数组的矩形,有分隔符的ASCII数据文件。
日记(或日志)文件的按键和结果文本输出。
使用fprintf等低级函数的专用ASCII文件。
MEX文件访问写入特定文本文件格式的C/C++或Fortran例程。
除此之外,还可以将数据导出到电子表格(Excel)。
将数字数组导出为有分隔符的ASCII数据文件有两种方法 -
使用save函数并指定-ascii限定符
使用dlmwrite函数
使用save函数的语法是:
save my_data.out num_array -ascii
其中,my_data.out是创建的分隔ASCII数据文件,num_array是一个数字数组,-ascii是说明符。
使用dlmwrite函数的语法是:
dlmwrite(‘mydata.out’,num_array,’\n’)
其中,my_data.out是分隔的ASCII数据文件,num_array是数组,dlm_char是分隔符。
示例
以下示例演示了这个概念。创建脚本文件并键入以下代码 -
num_array = [ 1 2 3 4 ; 4 5 6 7; 7 8 9 0];
save array_data1.out num_array -ascii;
type array_data1.out
dlmwrite('array_data2.out', num_array, ' ');
type array_data2.out执行上面示例代码,得到以下结果 -
Trial>> num_array = [ 1 2 3 4 ; 4 5 6 7; 7 8 9 0];
save array_data1.out num_array -ascii;
type array_data1.out
dlmwrite('array_data2.out', num_array, ' ');
type array_data2.out
1.0000000e+00 2.0000000e+00 3.0000000e+00 4.0000000e+00
4.0000000e+00 5.0000000e+00 6.0000000e+00 7.0000000e+00
7.0000000e+00 8.0000000e+00 9.0000000e+00 0.0000000e+00
1 2 3 4
4 5 6 7
7 8 9 0请注意,保存save -ascii命令和dlmwrite函数不能使用单元格数组作为输入。要从单元格数组的内容创建一个分隔的ASCII文件,可以 -
使用cell2mat函数将单元阵列转换为矩阵
或使用低级文件I/O函数导出单元格数组。
如果使用save函数将字符数组写入ASCII文件,则会将ASCII等效字符写入该文件。
例如,把一个单词hello写到一个文件 -
h = 'hello';
save textdata.out h -ascii
type textdata.outMATLAB执行上述语句并显示以下结果。这是8位ASCII格式的字符串“hello”的字符。
1.0400000e+02 1.0100000e+02 1.0800000e+02 1.0800000e+02 1.1100000e+02写到日记文件
日记文件是MATLAB会话的活动日志。diary函数在磁盘文件中创建会话的精确副本,不包括图形。
打开diary函数,键入 -
diary
或者,可以给出日志文件的名称,比如 -
diary diary.log
关闭日记函数 -
可以在文本编辑器中打开日记文件。
将数据导出到具有低级I/O的文本数据文件
到目前为止,我们已经导出数组。 但是,您可能需要创建其他文本文件,包括数字和字符数据的组合,非矩形输出文件或具有非ASCII编码方案的文件。为了实现这些目的,MATLAB提供了低级别的fprintf函数。
在低级I/O文件活动中,在导出之前,需要使用fopen函数打开或创建一个文件,并获取文件标识符。 默认情况下,fopen会打开一个只读访问的文件。所以应该指定写入或附加的权限,例如’w’或’a’。
处理文件后,需要用fclose(fid)函数关闭它。
以下示例演示了这一概念 -
示例
创建脚本文件并在其中键入以下代码 -
% create a matrix y, with two rows
x = 0:10:100;
y = [x; log(x)];
% open a file for writing
fid = fopen('logtable.txt', 'w');
% Table Header
fprintf(fid, 'Log Function\n\n');
% print values in column order
% two values appear on each row of the file
fprintf(fid, '%f %f\n', y);
fclose(fid);
% display the file created
type logtable.txt运行文件时,会显示以下结果 -
Log Function
0.000000 -Inf
10.000000 2.302585
20.000000 2.995732
30.000000 3.401197
40.000000 3.688879
50.000000 3.912023
60.000000 4.094345
70.000000 4.248495
80.000000 4.382027
90.000000 4.499810
100.000000 4.605170Matlab绘图
要使用plot函数来绘制图形,需要执行以下步骤:
- 通过指定要绘制函数的变量x的值的范围来定义x。
- 定义函数,y = f(x)
- 调用plot命令,如下:plot(x,y)
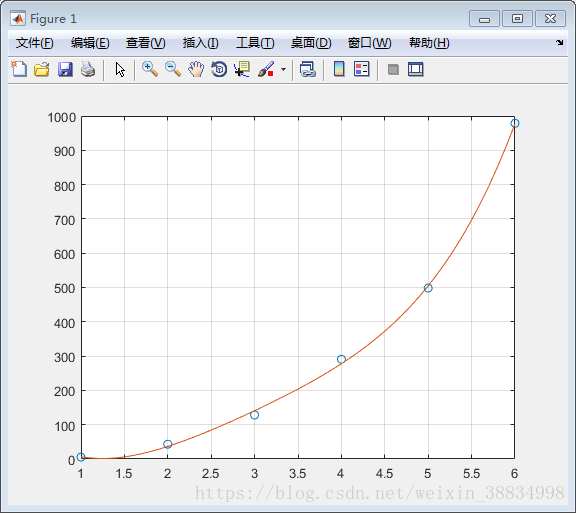
以下示例将演示该概念。下面绘制x的值范围是从0到100,使用简单函数y = x,增量值为5。
创建脚本文件并键入以下代码 -
x = [0:5:100];
y = x;
plot(x, y)下面再来一个例子来绘制函数y = x^2。 在这个例子中,将绘制两个具有相同函数的图,但是在第二次,将减小增量的值。请注意,当减少增量时,图形变得更平滑。
创建脚本文件并键入以下代码 -
x = [1 2 3 4 5 6 7 8 9 10];
x = [-100:10:100];
y = x.^2;
plot(x, y)在图上添加标题,标签,网格线和缩放
MATLAB允许沿x轴和y轴,网格线添加标题,标签,并且还可以调整轴来绘制图形。
- xlabel和ylabel命令沿x轴和y轴生成标签。
- title命令用于在图表上设置标题。
- grid on命令用于将网格线放在图形上。
- axis equal命令允许生成具有相同比例因子的绘图和两个轴上的空格。
- axis square命令生成一个方形图。
示例
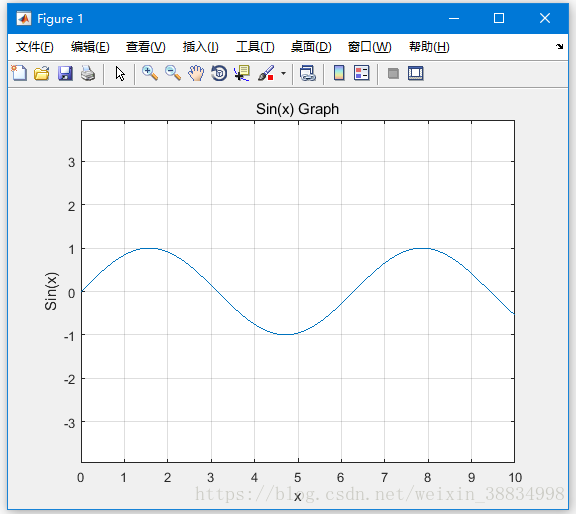
创建脚本文件并键入以下代码 -
x = [0:0.01:10];
y = sin(x);
plot(x, y), xlabel('x'), ylabel('Sin(x)'), title('Sin(x) Graph'),
grid on, axis equal在同一个图上绘制多个函数
可以在同一个图上绘制多个图形。以下示例演示了这一概念 -
示例
创建脚本文件并键入以下代码 -
x = [0 : 0.01: 10];
y = sin(x);
g = cos(x);
plot(x, y, x, g, '.-'), legend('Sin(x)', 'Cos(x)')MATLAB生成以下图表 -
在图上设置颜色
MATLAB提供了八个基本的颜色选项来绘制图形。 下表显示了颜色及其代码 -
| 代码 | 颜色 |
|---|---|
| w | White |
| k | Black |
| b | Blue |
| r | Red |
| c | Cyan |
| g | Green |
| m | Magenta |
| y | Yellow |
示例
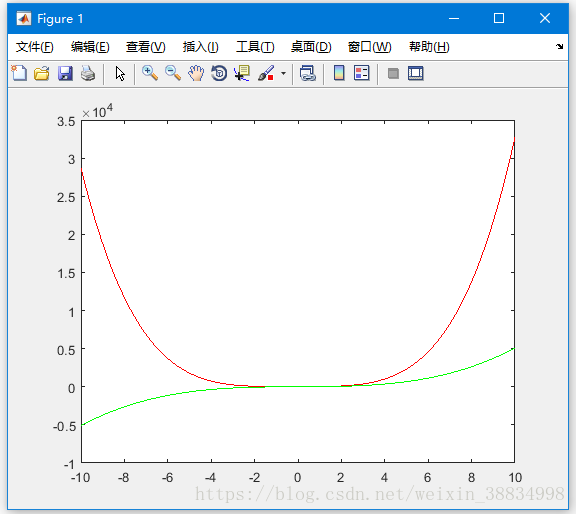
下面我们来绘制两个多项式的图形 -
y = 3*x.^4 + 2 * x.^3 + 7 * x.^2 + 2 * x + 9;
g = 5 * x.^3 + 9 * x + 2;
创建脚本文件并键入以下代码 -
x = [-10 : 0.01: 10];
y = 3*x.^4 + 2 * x.^3 + 7 * x.^2 + 2 * x + 9;
g = 5 * x.^3 + 9 * x + 2;
plot(x, y, 'r', x, g, 'g')作者:初生不惑 Java技术QQ群:227270512 / Linux QQ群:479429477
linuxprobe官方网站
要使用plot函数来绘制图形,需要执行以下步骤:
通过指定要绘制函数的变量x的值的范围来定义x。
定义函数,y = f(x)
调用plot命令,如下:plot(x,y)
以下示例将演示该概念。下面绘制x的值范围是从0到100,使用简单函数y = x,增量值为5。
创建脚本文件并键入以下代码 -
x = [0:5:100];
y = x;
plot(x, y)
MATLAB
执行上面示例代码,得到以下结果 -
下面再来一个例子来绘制函数y = x^2。 在这个例子中,将绘制两个具有相同函数的图,但是在第二次,将减小增量的值。请注意,当减少增量时,图形变得更平滑。
创建脚本文件并键入以下代码 -
x = [1 2 3 4 5 6 7 8 9 10];
x = [-100:10:100];
y = x.^2;
plot(x, y)
MATLAB
执行上面示例代码,得到以下结果 -
更改代码,减少增量为2 -
在图上添加标题,标签,网格线和缩放
MATLAB允许沿x轴和y轴,网格线添加标题,标签,并且还可以调整轴来绘制图形。
xlabel和ylabel命令沿x轴和y轴生成标签。
title命令用于在图表上设置标题。
grid on命令用于将网格线放在图形上。
axis equal命令允许生成具有相同比例因子的绘图和两个轴上的空格。
axis square命令生成一个方形图。
示例
创建脚本文件并键入以下代码 -
x = [0:0.01:10];
y = sin(x);
plot(x, y), xlabel(‘x’), ylabel(‘Sin(x)’), title(‘Sin(x) Graph’),
grid on, axis equal
MATLAB
MATLAB生成以下图表 -
在同一个图上绘制多个函数
可以在同一个图上绘制多个图形。以下示例演示了这一概念 -
示例
创建脚本文件并键入以下代码 -
x = [0 : 0.01: 10];
y = sin(x);
g = cos(x);
plot(x, y, x, g, ‘.-‘), legend(‘Sin(x)’, ‘Cos(x)’)
MATLAB
MATLAB生成以下图表 -
在图上设置颜色
MATLAB提供了八个基本的颜色选项来绘制图形。 下表显示了颜色及其代码 -
代码 颜色
w White
k Black
b Blue
r Red
c Cyan
g Green
m Magenta
y Yellow
示例
下面我们来绘制两个多项式的图形 -
创建脚本文件并键入以下代码 -
x = [-10 : 0.01: 10];
y = 3*x.^4 + 2 * x.^3 + 7 * x.^2 + 2 * x + 9;
g = 5 * x.^3 + 9 * x + 2;
plot(x, y, ‘r’, x, g, ‘g’)
MATLAB
执行上面示例代码,MATLAB生成以下图表 -
设置轴刻度
axis命令用来设置轴刻度。可以通过以下方式使用axis命令为x和y轴提供最小和最大值:
axis ( [xmin xmax ymin ymax] )示例
创建脚本文件并键入以下代码 -
x = [0 : 0.01: 10];
y = exp(-x).* sin(2*x + 3);
plot(x, y,'m'), axis([0 10 -1 1])生成子图
当在同一个图中创建一个绘图数组时,这些图中的每一个图称为子图。 subplot命令用于创建子图。
该命令的语法是 -
subplot(m, n, p)MATLAB
其中,m和n是绘图数组的行数和列数,p表示放置指定图形的位置。
使用subplot命令创建的每个曲线都可以有自己的特点。 以下示例演示了这一概念 -
示例
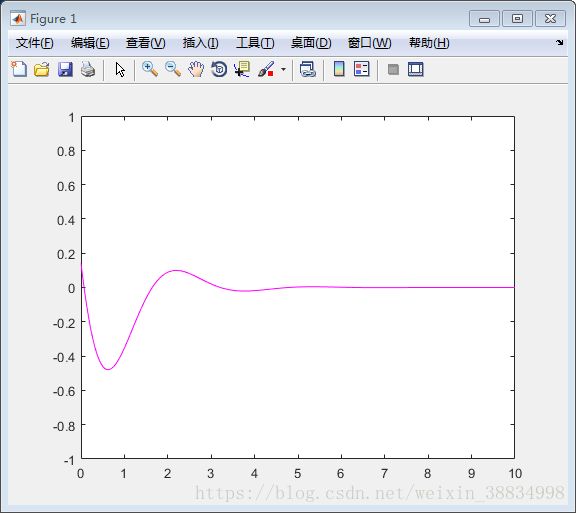
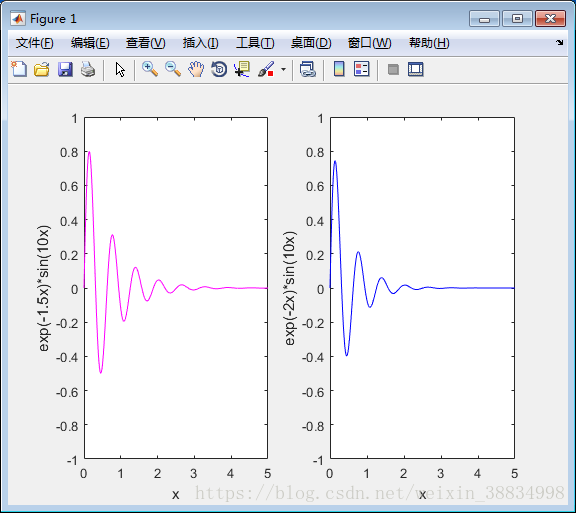
下面示例将生成两个区域块 -
y = exp(-1.5*x).*sin(10*x);
y = exp(-2*x).*sin(10*x);
创建脚本文件并键入以下代码 -
x = [0:0.01:5];
y = exp(-1.5*x).*sin(10*x);
subplot(1,2,1)
plot(x,y,'m'),xlabel('x'),ylabel('exp(-1.5x)*sin(10x)'),axis([0 5 -1 1])
y = exp(-2*x).*sin(10*x);
subplot(1,2,2)
plot(x,y,'b'), xlabel('x'),ylabel('exp(-2x)*sin(10x)'),axis([0 5 -1 1])Matlab图形
本章将继续探讨MATLAB的绘图和图形函数功能。下面将会讨论 -
- 绘制条形图
- 绘制轮廓
- 三维图
绘制条形图
bar命令绘制二维条形图,下面举个例子来演示如何使用。
示例
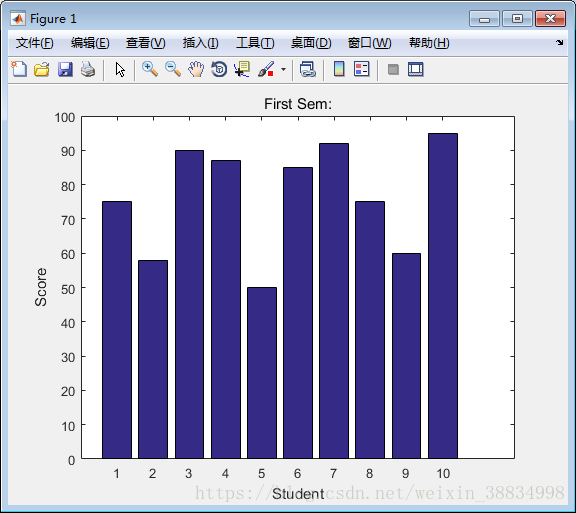
假设有10名学生,这些学生某次考试获得分数是:75,58,90,87,50,85,92,75,60和95,使用这此分数来绘制条形图如下。
创建脚本文件并键入以下代码 -
x = [1:10];
y = [75, 58, 90, 87, 50, 85, 92, 75, 60, 95];
bar(x,y), xlabel('Student'),ylabel('Score'),
title('First Sem:')
print -deps graph.eps运行文件时,MATLAB显示以下条形图 -
绘制等高线
两个变量的函数的轮廓线是一个曲线,函数有一个恒定值。等高线用于通过连接等于高于某一水平的点(如平均海平面)来创建轮廓图。
MATLAB提供了绘制轮廓图的contour函数。
示例
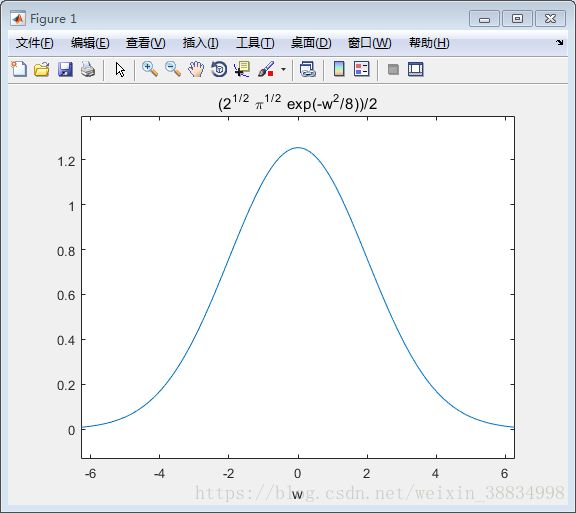
下面演示如何生成一个轮廓图,显示给定函数g = f(x,y)的轮廓线。该函数有两个变量。 所以,必须生成两个独立的变量,即两个数据集x和y。 这可以通过调用meshgrid命令完成。
meshgrid命令用于生成在每种情况下给出x和y范围以及增量规范的元素矩阵。
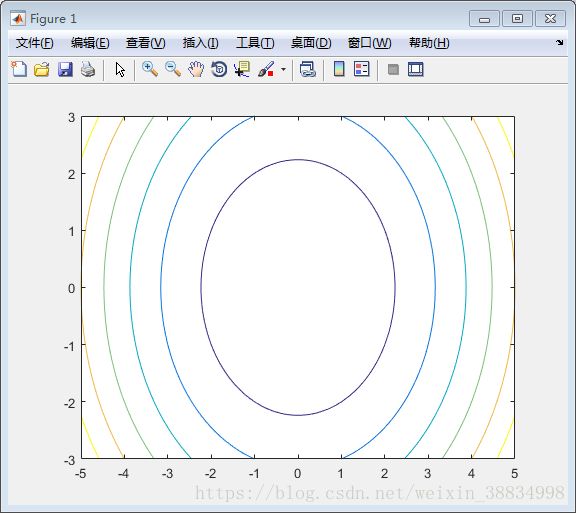
绘制函数g = f(x,y),其中-5≤x≤5,-3≤y≤3。对于这两个值,递增0.1。变量设置为 -
[x,y] = meshgrid(–5:0.1:5, –3:0.1:3);最后,需要分配这个函数。使用函数为:x^2 + y^2(注:x和y的平方之和)
创建脚本文件并键入以下代码 -
[x,y] = meshgrid(-5:0.1:5,-3:0.1:3); %independent variables
g = x.^2 + y.^2; % our function
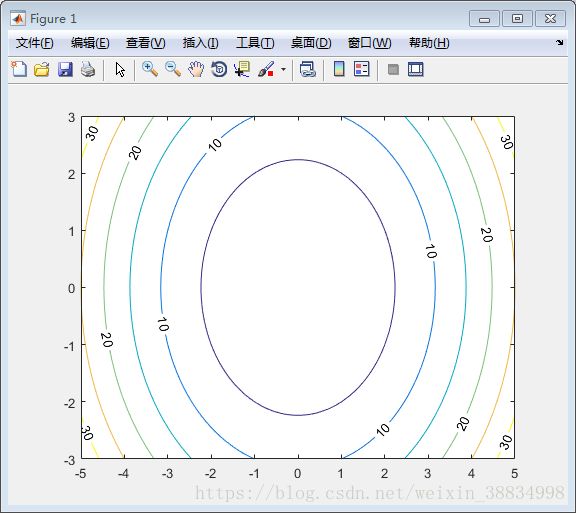
contour(x,y,g) % call the contour function
print -deps graph.eps执行上面示例代码,得到以下结果 -
下面再修改一下代码,使地图上变得有数据标识 -
[x,y] = meshgrid(-5:0.1:5,-3:0.1:3); %independent variables
g = x.^2 + y.^2; % our function
[C, h] = contour(x,y,g); % call the contour function
set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2)
print -deps graph.eps执行上面示例代码,得到以下结果 -
三维图
三维图基本上显示的是由两个变量g = f(x,y)中的函数定义的表面。
像之前一样,要定义g,首先使用meshgrid命令在函数的域上创建一组(x,y)点。 接下来,分配函数本身。 最后,使用surf命令创建一个曲面图。
以下示例演示了这一概念 -
示例
为以下函数创建一个3D曲面图 -
创建脚本文件并键入以下代码 -
[x,y] = meshgrid(-2:.2:2);
g = x .* exp(-x.^2 - y.^2);
surf(x, y, g)
print -deps graph.eps运行文件时,MATLAB显示以下三维图 -
也可以使用mesh命令生成三维表面。 但是,surf命令显示连接线和表面的颜色,而mesh命令创建一个线框表面,带有连接定义点的彩色线。
改成mesh显示如下
mesh(x, y, g)Matlab代数(方程求解)
到目前为止,我们已经看到所有的例子都在MATLAB以及它的GNU,或者称为Octave。 但是,为了求解基本代数方程,MATLAB和Octave都不同,所以这里将分别介绍MATLAB和Octave。
我们还将讨论代数表达式的分解和简化。
在MATLAB中求解基本代数方程
solve函数用于求解代数方程。 在其最简单的形式中,solve函数将引用中的方程式作为参数。
例如,在等式x-5 = 0中求解x,参考以下代码实现 -
solve('x-178=0')MATLAB将执行上述语句并返回以下结果 -
Trial>> solve('x-178=0')
ans =
178也可以这样调用solve函数 -
Trial>> solve('x-110 = 0')
ans =
110甚至可以不用包括方程的右侧部分 -
Trial>> solve('x-110')
ans =
110如果方程式涉及多个符号,则默认情况下,MATLAB假定正在求解x,但是,solve函数具有另一种形式 -
solve(equation, variable)其中,也可以涉及到变量。
例如,要求解v - u - 3t^2 = 0(这里为t的平方),对于v,在这种情况下,应该书写为 -
solve('v-u-3*t^2=0', 'v')MATLAB执行上述语句将返回以下结果 -
ans =
3*t^2 + u求解代数中的基本代数方程
roots函数用于求解代数中的代数方程,可以重写上面的例子如下:
例如,要在等式x-5 = 0中求解x的值 -
roots([1, -5])执行上面示例代码,得到以下结果 -
Trial>> roots([1, -5])
ans =
5也可以这样调用roots函数 -
y = roots([1, -5])执行上面示例代码,得到以下结果 -
Trial>> y = roots([1, -5])
y =
5在MATLAB中求解二次方程
solve函数也可以用来求解高阶方程。通常用于求解二次方程。 该函数返回数组中方程的根。
以下示例求解二次方程x^2 -7x +12 = 0(注:x^2表示x的平方)。创建脚本文件并键入以下代码 -
eq = 'x^2 -7*x + 12 = 0';
s = solve(eq);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));执行上面示例代码,得到以下结果 -
Trial>> eq = 'x^2 -7*x + 12 = 0';
s = solve(eq);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));
The first root is:
3
The second root is:
4在Octave中求解二次方程
以下示例解决Octave中的二次方程x^2-7x +12 = 0。创建脚本文件并键入以下代码 -
s = roots([1, -7, 12]);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));执行上面示例代码,得到以下结果 -
Trial>> s = roots([1, -7, 12]);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));
The first root is:
4
The second root is:
3求解MATLAB中的高阶方程
solve函数也可以解决高阶方程。例如,下面演示求解(x-3)^2(x-7)= 0(注:(x-3)^2表示(x-3)的平方)的三次方程 -
MATLAB执行上述语句将返回以下结果 -
ans =
3
3
7在较高阶方程的情况下,根很长,包含很多项。可以通过将这些根的数值转换为double来获得数值。 以下示例解决四阶方程x^4 - 7x^3 + 3x^2 - 5x + 9 = 0(注:x^4表示x的4次方)。
创建脚本文件并键入以下代码 -
eq = 'x^4 - 7*x^3 + 3*x^2 - 5*x + 9 = 0';
s = solve(eq);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));
disp('The third root is: '), disp(s(3));
disp('The fourth root is: '), disp(s(4));
% converting the roots to double type
disp('Numeric value of first root'), disp(double(s(1)));
disp('Numeric value of second root'), disp(double(s(2)));
disp('Numeric value of third root'), disp(double(s(3)));
disp('Numeric value of fourth root'), disp(double(s(4)));MATLAB执行上述语句将返回以下结果 -
The first root is:
root(z^4 - 7*z^3 + 3*z^2 - 5*z + 9, z, 1)
The second root is:
root(z^4 - 7*z^3 + 3*z^2 - 5*z + 9, z, 2)
The third root is:
root(z^4 - 7*z^3 + 3*z^2 - 5*z + 9, z, 3)
The fourth root is:
root(z^4 - 7*z^3 + 3*z^2 - 5*z + 9, z, 4)
Numeric value of first root
1.0598
Numeric value of second root
6.6304
Numeric value of third root
-0.3451 - 1.0778i
Numeric value of fourth root
-0.3451 + 1.0778i请注意,最后两个根是复数。
在Octave中求解高阶方程
以下示例示解四阶方程:x^4 - 7x3 + 3x^2 - 5x + 9 = 0。
创建脚本文件并键入以下代码 -
v = [1, -7, 3, -5, 9];
s = roots(v);
% converting the roots to double type
disp('Numeric value of first root'), disp(double(s(1)));
disp('Numeric value of second root'), disp(double(s(2)));
disp('Numeric value of third root'), disp(double(s(3)));
disp('Numeric value of fourth root'), disp(double(s(4)));MATLAB执行上述语句将返回以下结果 -
Trial>> v = [1, -7, 3, -5, 9];
s = roots(v);
% converting the roots to double type
disp('Numeric value of first root'), disp(double(s(1)));
disp('Numeric value of second root'), disp(double(s(2)));
disp('Numeric value of third root'), disp(double(s(3)));
disp('Numeric value of fourth root'), disp(double(s(4)));
Numeric value of first root
6.6304
Numeric value of second root
1.0598
Numeric value of third root
-0.3451 + 1.0778i
Numeric value of fourth root
-0.3451 - 1.0778iMATLAB中求解方程组
solve函数也可用于生成包含多个变量的方程组的解。下面来看一个简单的例子来说明这一点。
下面来求解方程式 -
5x + 9y = 5
3x – 6y = 4
创建脚本文件并键入以下代码 -
s = solve('5*x + 9*y = 5','3*x - 6*y = 4');
x = s.x
y = s.yMATLAB执行上述语句将返回以下结果 -
x =
22/19
y =
-5/57同样,可以示解决更大的线性系统。 考虑以下一组方程式 -
x + 3y -2z = 5
3x + 5y + 6z = 7
2x + 4y + 3z = 8在Octave中求解方程组
还可以使用不同的方法来示解n未知数的n线性方程组。下面来看一个简单的例子来说明这一点。
假设要示解方程式 -
5x + 9y = 5
3x – 6y = 4这种线性方程组可以写成单矩阵方程Ax = b,其中A是系数矩阵,b是包含线性方程右边的列向量,x是表示解的方法的列向量。如下图所示 -
创建脚本文件并键入以下代码 -
A = [5, 9; 3, -6];
b = [5;4];
A \ b执行上面示例代码,得到以下结果 -
ans =
1.157895
-0.087719同样,可以示解下面给出的较大的方程组 -
x + 3y -2z = 5
3x + 5y + 6z = 7
2x + 4y + 3z = 8A = [1,3,-2;3,5,6;2,4,3];
b = [5;7;8];
A\b结果
ans =
-15.0000
8.0000
2.0000在MATLAB中扩展和集合方程
expand 和 collect函数分别扩展和集合方程。以下示例演示了这些概念 -
当使用许多符号功能时,应该声明变量为符号。
创建脚本文件并键入以下代码 -
syms x %symbolic variable x
syms y %symbolic variable x
% expanding equations
expand((x-5)*(x+9))
expand((x+2)*(x-3)*(x-5)*(x+7))
expand(sin(2*x))
expand(cos(x+y))
% collecting equations
collect(x^3 *(x-7))
collect(x^4*(x-3)*(x-5))执行上面示例代码,得到以下结果 -
ans =
x^2 + 4*x - 45
ans =
x^4 + x^3 - 43*x^2 + 23*x + 210
ans =
2*cos(x)*sin(x)
ans =
cos(x)*cos(y) - sin(x)*sin(y)
ans =
x^4 - 7*x^3
ans =
x^6 - 8*x^5 + 15*x^4在Octave扩展和集合方程
需要有symbolic包,它提供了expand和collect函数来分别扩展和集合方程。 以下示例演示了这些概念 -
当使用许多符号功能时,应该声明变量是符号,但是Octave具有不同的方法来定义符号变量。注意使用的是Sin和Cos,它们是定义在symbolic包中的。
创建脚本文件并键入以下代码 -
% first of all load the package, make sure its installed.
pkg load symbolic
% make symbols module available
symbols
% define symbolic variables
x = sym ('x');
y = sym ('y');
z = sym ('z');
% expanding equations
expand((x-5)*(x+9))
expand((x+2)*(x-3)*(x-5)*(x+7))
expand(Sin(2*x))
expand(Cos(x+y))
% collecting equations
collect(x^3 *(x-7), z)
collect(x^4*(x-3)*(x-5), z)
Shell
运行文件时,会显示以下结果 -
ans =
-45.0+x^2+(4.0)*x
ans =
210.0+x^4-(43.0)*x^2+x^3+(23.0)*x
ans =
sin((2.0)*x)
ans =
cos(y+x)
ans =
x^(3.0)*(-7.0+x)
ans =
(-3.0+x)*x^(4.0)*(-5.0+x)代数表达式的因式分解和简化
因子函数将表达式分解,简化函数简化表达式。 以下示例演示了这一概念 -
示例
创建脚本文件并键入以下代码 -
syms x
syms y
factor(x^3 - y^3)
f = factor(y^2*x^2,x)
simplify((x^4-16)/(x^2-4))执行上面示例代码,得到以下结果 -
Trial>> factorization
ans =
[ x - y, x^2 + x*y + y^2]
f =
[ y^2, x, x]
ans =
x^2 + 4Matlab微积分
MATLAB提供了解决微分和积分微积分的各种方法,求解任何程度的微分方程和极限计算。可以轻松绘制复杂功能的图形,并通过求解原始功能以及其衍生来检查图形上的最大值,最小值和其他固定点。
本章将介绍微积分问题。在本章中,将讨论预演算法,即计算功能限制和验证限制属性。
在下一章微分中,将计表达式的导数,并找到一个图的局部最大值和最小值。我们还将讨论求解微分方程。
最后,在“整合/集成”一章中,我们将讨论积分微积分。
计算极限
MATLAB提供计算极限的limit函数。在其最基本的形式中,limit函数将表达式作为参数,并在独立变量为零时找到表达式的极限。
例如,要计算函数f(x)=(x^3 + 5)/(x^4 + 7)的极限,因为x趋向于零。
syms x
limit((x^3 + 5)/(x^4 + 7))执行上面示例代码,得到以下结果 -
Trial>> syms x
limit((x^3 + 5)/(x^4 + 7))
ans =
5/7limit函数落在符号计算域; 需要使用syms函数来告诉MATLAB正在使用的符号变量。还可以计算函数的极限,因为变量趋向于除零之外的某个数字。要计算 -
![]()
可使用带有参数的limit命令。第一个是表达式,第二个是数字 - x表示接近,这里它是a。
例如,要计算函数f(x)=(x-3)/(x-1)的极限,因为x倾向于1。
limit((x - 3)/(x-1),1)执行上面示例代码,得到以下结果 -
ans =
NaN下面再看另外一个例子,
limit(x^2 + 5, 3)执行上面示例代码,得到以下结果 -
ans =
14使用Octave计算极限
以下是Octave版本的上述示例使用symbolic包,尝试执行并比较结果 -
pkg load symbolic
symbols
x=sym("x");
subs((x^3+5)/(x^4+7),x,0)执行上面示例代码,得到以下结果 -
ans =
0.7142857142857142857验证极限的基本属性
代数极限定理提供了极限的一些基本属性。这些属性如下 -
下面来考虑两个函数 -
f(x) = (3x + 5)/(x - 3)
g(x) = x^2 + 1.下面计算函数的极限,这两个函数的x趋向于5,并使用这两个函数和MATLAB验证极限的基本属性。
例子
创建脚本文件并在其中键入以下代码 -
syms x
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1 = limit(f, 4)
l2 = limit (g, 4)
lAdd = limit(f + g, 4)
lSub = limit(f - g, 4)
lMult = limit(f*g, 4)
lDiv = limit (f/g, 4)执行上面示例代码,得到以下结果 -
l1 =
17
l2 =
17
lAdd =
34
lSub =
0
lMult =
289
lDiv =
1使用Octave验证极限的基本属性
以下是Octave版本的上述示例使用symbolic包,尝试执行并比较结果 -
pkg load symbolic
symbols
x = sym("x");
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1=subs(f, x, 4)
l2 = subs (g, x, 4)
lAdd = subs (f+g, x, 4)
lSub = subs (f-g, x, 4)
lMult = subs (f*g, x, 4)
lDiv = subs (f/g, x, 4)执行上面示例代码,得到以下结果 -
l1 =
17.0
l2 =
17.0
lAdd =
34.0
lSub =
0.0
lMult =
289.0
lDiv =
1.0左右边界极限
当函数对变量的某个特定值具有不连续性时,该点不存在极限。 换句话说,当x = a时,函数f(x)的极限具有不连续性,当x的值从左侧接近x时,x的值不等于x从右侧接近的极限值。
对于x
f(x) = (x - 3)/|x - 3|下面将显示
![]()
不存在。MATLAB帮助我们以两种方式说明事实 -
- 通过绘制函数图并显示不连续性。
- 通过计算极限并显示两者都不同。
通过将字符串“left”和“right”作为最后一个参数传递给limit命令来计算左侧和右侧的极限。
例子
创建脚本文件并在其中键入以下代码 -
f = (x - 3)/abs(x-3);
ezplot(f,[-1,5])
l = limit(f,x,3,'left')
r = limit(f,x,3,'right')MATLAB
执行上面示例代码,得到以下结果 -
显示以下输出结果 -
Trial>>
Trial>> f = (x - 3)/abs(x-3);
ezplot(f,[-1,5])
l = limit(f,x,3,'left')
r = limit(f,x,3,'right')
l =
-1
r =
1Matlab微分和导数
MATLAB提供用于计算符号导数的diff命令。 以最简单的形式,将要微分的功能传递给diff命令作为参数。
例如,计算函数的导数的方程式 -
例子
创建脚本文件并在其中键入以下代码 -
syms t
f = 3*t^2 + 2*t^(-2);
diff(f)执行上面示例代码,得到以下结果 -
Trial>> syms t
f = 3*t^2 + 2*t^(-2);
diff(f)
ans =
6*t - 4/t^3以下是使用Octave 计算的写法 -
pkg load symbolic
symbols
t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)执行上面示例代码,得到以下结果 -
ans =
6*t - 4/t^3基本微分规则的验证
下面简要说明微分规则的各种方程或规则,并验证这些规则。 为此,我们将写一个第一阶导数f’(x)和二阶导数f“(x)。
以下是微分的规则 -
规则 - 1
对于任何函数f和g,任何实数a和b是函数的导数:
h(x) = af(x) + bg(x)相对于x,由h’(x) = af’(x) + bg’(x)给出。
规则 - 2
sum和subtraction规则表述为:如果f和g是两个函数,则f’和g’分别是它们的导数,如下 -
(f + g)’ = f’ + g’
(f - g)’ = f’ - g’
规则 - 3
product规则表述为:如果f和g是两个函数,则f’和g’分别是它们的导数,如下 -
(f.g)’ = f’.g + g’.f
规则 - 4
quotient规则表明,如果f和g是两个函数,则f’和g’分别是它们的导数,那么 -
规则 - 5
多项式或基本次幂规则表述为:如果y = f(x)= x^n,则 -
这个规则的直接结果是任何常数的导数为零,即如果y = k,那么为任何常数 -
f’ = 0
规则 - 6
chain规则表述为 - 相对于x的函数h(x)= f(g(x))的函数的导数是 -
h'(x)= f'(g(x)).g'(x)例子
创建脚本文件并在其中键入以下代码 -
syms x
syms t
f = (x + 2)*(x^2 + 3)
der1 = diff(f)
f = (t^2 + 3)*(sqrt(t) + t^3)
der2 = diff(f)
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = diff(f)
f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = diff(f)
f = (x^2 + 1)^17
der5 = diff(f)
f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = diff(f)执行上面示例代码,得到 以下结果 -
f =
(x^2 + 3)*(x + 2)
der1 =
2*x*(x + 2) + x^2 + 3
f =
(t^(1/2) + t^3)*(t^2 + 3)
der2 =
(t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3)
f =
(x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 =
(2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1)
f =
(2*x^2 + 3*x)/(x^3 + 1)
der4 =
(4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2
f =
(x^2 + 1)^17
der5 =
34*x*(x^2 + 1)^16
f =
1/(t^3 + 3*t^2 + 5*t - 9)^6
der6 =
-(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7以下是对上面示例的Octave写法 -
pkg load symbolic
symbols
x=sym("x");
t=sym("t");
f = (x + 2)*(x^2 + 3)
der1 = differentiate(f,x)
f = (t^2 + 3)*(t^(1/2) + t^3)
der2 = differentiate(f,t)
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = differentiate(f,x)
f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = differentiate(f,x)
f = (x^2 + 1)^17
der5 = differentiate(f,x)
f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = differentiate(f,t)指数,对数和三角函数的导数
下表提供了常用指数,对数和三角函数的导数,
例子
创建脚本文件并在其中键入以下代码 -
syms x
y = exp(x)
diff(y)
y = x^9
diff(y)
y = sin(x)
diff(y)
y = tan(x)
diff(y)
y = cos(x)
diff(y)
y = log(x)
diff(y)
y = log10(x)
diff(y)
y = sin(x)^2
diff(y)
y = cos(3*x^2 + 2*x + 1)
diff(y)
y = exp(x)/sin(x)
diff(y)执行上面示例代码,得到以下结果 -
y =
exp(x)
ans =
exp(x)
y =
x^9
ans =
9*x^8
y =
sin(x)
ans =
cos(x)
y =
tan(x)
ans =
tan(x)^2 + 1
y =
cos(x)
ans =
-sin(x)
y =
log(x)
ans =
1/x
y =
log(x)/log(10)
ans =
1/(x*log(10))
y =
sin(x)^2
ans =
2*cos(x)*sin(x)
y =
cos(3*x^2 + 2*x + 1)
ans =
-sin(3*x^2 + 2*x + 1)*(6*x + 2)
y =
exp(x)/sin(x)
ans =
exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2以下代码是上面代码的Octave写法 -
pkg load symbolic
symbols
x = sym("x");
y = Exp(x)
differentiate(y,x)
y = x^9
differentiate(y,x)
y = Sin(x)
differentiate(y,x)
y = Tan(x)
differentiate(y,x)
y = Cos(x)
differentiate(y,x)
y = Log(x)
differentiate(y,x)
% symbolic packages does not have this support
%y = Log10(x)
%differentiate(y,x)
y = Sin(x)^2
differentiate(y,x)
y = Cos(3*x^2 + 2*x + 1)
differentiate(y,x)
y = Exp(x)/Sin(x)
differentiate(y,x)计算高阶导数
要计算函数f的较高导数,可使用diff(f,n)。
计算函数的二阶导数公式为 -
![]()
f = x*exp(-3*x);
diff(f, 2)MATLAB执行上面代码将返回以下结果 -
ans =
9*x*exp(-3*x) - 6*exp(-3*x)以下是使用Octave重写上面示例,代码如下 -
pkg load symbolic
symbols
x = sym("x");
f = x*Exp(-3*x);
differentiate(f, x, 2)例子
在这个例子中,要解决一个问题。由给定函数y = f(x)= 3sin(x)+ 7cos(5x),来找出方程f“+ f = -5cos(2x)是否成立。
创建脚本文件并在其中键入以下代码 -
syms x
y = 3*sin(x)+7*cos(5*x); % defining the function
lhs = diff(y,2)+y; %evaluting the lhs of the equation
rhs = -5*cos(2*x); %rhs of the equation
if(isequal(lhs,rhs))
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);运行文件时,会显示以下结果 -
No, the equation does not hold true
Value of LHS is:
-168*cos(5*x)以上是上面示例的Octave写法 -
pkg load symbolic
symbols
x = sym("x");
y = 3*Sin(x)+7*Cos(5*x); % defining the function
lhs = differentiate(y, x, 2) + y; %evaluting the lhs of the equation
rhs = -5*Cos(2*x); %rhs of the equation
if(lhs == rhs)
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);查找曲线的最大和最小值
如果正在搜索图形的局部最大值和最小值,基本上是在特定地点的函数图上或符号变量的特定值范围内查找最高点或最低点。
对于函数y = f(x),图形具有零斜率的图上的点称为固定点。 换句话说,固定点是f’(x)= 0。
要找到微分的函数的固定点,需要将导数设置为零并求解方程。
示例
要找到函数f(x)= 2x3 + 3x2 - 12x + 17的固定点
可参考以下步骤 -
首先输入函数并绘制图,代码如下 -
syms x
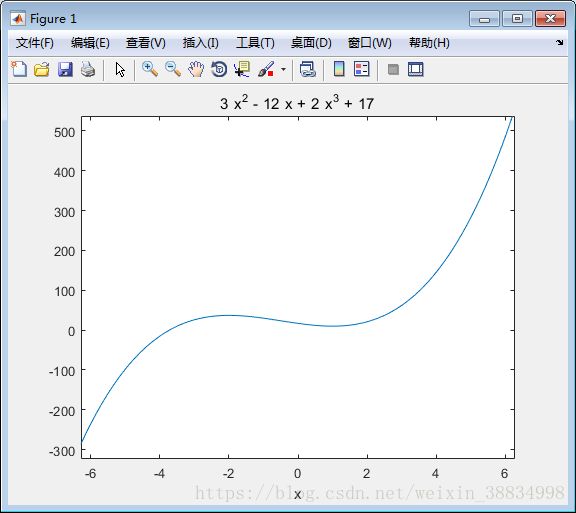
y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function
ezplot(y)执行上面示例代码,得到以下结果 -
以上是上面示例的Octave写法 -
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y)
print -deps graph.eps我们的目标是在图上找到一些局部最大值和最小值,假设要找到图中间隔在[-2,2]的局部最大值和最小值。参考以下示例代码 -
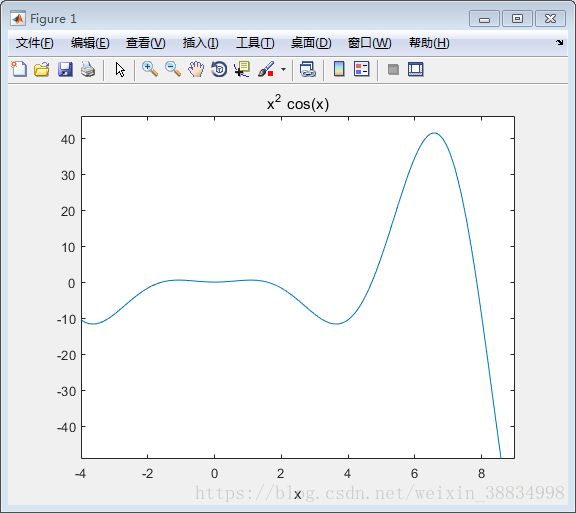
syms x
y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function
ezplot(y, [-2, 2])执行上面示例代码,得到以下结果 -
以下是上面示例的Octave写法 -
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y, [-2, 2])
print -deps graph.eps接下来,需要计算导数。
g = diff(y)MATLAB执行代码并返回以下结果 -
g =
6*x^2 + 6*x - 12以下是上面示例的Octave写法 -
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)接下来求解导数函数g,得到它变为零的值。
s = solve(g)MATLAB执行代码并返回以下结果 -
s =
1
-2以下是上面示例的Octave写法 -
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])这与我们设想情节一致。 因此,要评估临界点x = 1,-2处的函数f。可以使用subs命令替换符号函数中的值。
subs(y, 1), subs(y, -2)MATLAB执行代码并返回以下结果 -
ans =
10
ans =
37以下是上面示例的Octave写法 -
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])
subs(y, x, 1), subs(y, x, -2)因此,在间隔[-2,2]中函数f(x)= 2x^3 + 3x^2 - 12x + 17的最小值和最大值分别为10和37。
求解微分方程
MATLAB提供了用于求解微分方程的dsolve命令。
找到单个方程的解的最基本的dsolve命令形式是 -
dsolve('eqn')其中eqn是用于输入方程式的文本串。
它返回一个符号解,其中包含一组任意常量,MATLAB标记C1,C2等等。
还可以为问题指定初始和边界条件,以逗号分隔的列表遵循以下公式:
dsolve('eqn','cond1', 'cond2',…)为了使用dsolve命令,导数用D表示。例如,像f’(t)= -2 * f + cost(t)这样的等式输入为 -
'Df = -2*f + cos(t)'较高阶导数由D导数的顺序表示。
例如,方程f”(x) + 2f’(x) = 5sin3x应输入为 -
'D2y + 2Dy = 5*sin(3*x)'下面来看一个一阶微分方程的简单例子:y’= 5y。
s = dsolve('Dy = 5*y')MATLAB执行代码并返回以下结果 -
s =
C2*exp(5*t)再来一个二阶微分方程的例子:y“-y = 0,y(0)= -1,y’(0)= 2。
dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')MATLAB执行代码并返回以下结果 -
ans =
exp(t)/2 - (3*exp(-t))/2Matlab整合集成
整合(或也叫作集成)涉及两种本质上不同类型的问题。
- 第一种类型问题是给出了函数的导数,并且想要找到该函数。所以基本上扭转了差异化的过程。
这种反向过程被称为抗分化,或者找到原始函数,或者找到不确定的积分。 - 第二种类型问题是涉及相当多的非常小的数量,然后随着数量的大小接近于零,而术语的数量趋向于无穷大。这个过程导致了定积分的定义。
确定的积分用于查找区域,体积,重心,转动惯量,由力完成的工作以及许多其他应用。
使用MATLAB找到不确定的积分
根据定义,如果函数f(x)的导数是f’(x),那么可以说f’(x)相对于x的不确定积分是f(x)。 例如,由于x^2的导数(相对于x)为2x,可以说2x的不确定积分是x^2。
在符号中 -
![]()
因此可相当于 -
不确定积分并不是唯一的,因为对于常数c的任何值,x^2 + c的导数也将是2x。
这用符号表示为 -
其中,c被称为“任意常数”。
MATLAB提供了一个用于计算表达式积分的int命令。 为了得出一个函数的无限积分的表达式,它的写法为 -
int(f);例如,引用之前的例子 -
syms x
int(2*x)MATLAB执行上述语句将返回以下结果 -
ans =
x^2示例1
在这个例子中,有一些常用表达式的积分。 创建脚本文件并在其中键入以下代码 -
syms x n
int(sym(x^n))
f = 'sin(n*t)'
int(sym(f))
syms a t
int(a*cos(pi*t))
int(a^x)MATLAB执行上述语句将返回以下结果 -
ans =
piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)])
f =
sin(n*t)
ans =
-cos(n*t)/n
ans =
(a*sin(pi*t))/pi
ans =
a^x/log(a)示例2
创建脚本文件并在其中键入以下代码 -
syms x n
int(cos(x))
int(exp(x))
int(log(x))
int(x^-1)
int(x^5*cos(5*x))
pretty(int(x^5*cos(5*x)))
int(x^-5)
int(sec(x)^2)
pretty(int(1 - 10*x + 9 * x^2))
int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2)
pretty(int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2))请注意,pretty函数返回表达式的更可读格式。
MATLAB执行上述语句将返回以下结果 -
ans =
sin(x)
ans =
exp(x)
ans =
x*(log(x) - 1)
ans =
log(x)
ans =
(24*cos(5*x))/3125 + (24*x*sin(5*x))/625 - (12*x^2*cos(5*x))/125 + (x^4*cos(5*x))/5 - (4*x^3*sin(5*x))/25 + (x^5*sin(5*x))/5
2 4
24 cos(5 x) 24 x sin(5 x) 12 x cos(5 x) x cos(5 x)
----------- + ------------- - -------------- + ----------- -
3125 625 125 5
3 5
4 x sin(5 x) x sin(5 x)
------------- + -----------
25 5
ans =
-1/(4*x^4)
ans =
tan(x)
2
x (3 x - 5 x + 1)
ans =
- (7*x^6)/12 - (3*x^5)/5 + (5*x^4)/8 + x^3/2
6 5 4 3
7 x 3 x 5 x x
- ---- - ---- + ---- + --
12 5 8 2MATLAB执行上述语句将返回以下结果 -
Shell
使用MATLAB查找定积分
根据定义,定积分基本上是一个总和的极限。 我们使用定积分来查找曲线和x轴之间的面积以及两条曲线之间的面积。定量积分也可用于其他情况,其中所需数量可以表示为总和的极限。
通过传递要计算积分的极限,int函数可用于定积分。
参考公式 -
它的写法是 -
int(x, a, b)例如,要计算的值是 -
因此,可以书写为 -
int(x, 4, 9)MATLAB执行上述语句将返回以下结果 -
ans =
65/2以下是以上示例的Octave写法 -
pkg load symbolic
symbols
x = sym("x");
f = x;
c = [1, 0];
integral = polyint(c);
a = polyval(integral, 9) - polyval(integral, 4);
display('Area: '), disp(double(a));可以使用Octave提供的quad()函数编写另一个替代求解代码,如下所示:
pkg load symbolic
symbols
f = inline("x");
[a, ierror, nfneval] = quad(f, 4, 9);
display('Area: '), disp(double(a));示例1
下面来计算x轴和曲线y = x^3-2x + 5和纵坐标x = 1和x = 2之间的面积。
所需面积由公式计算 -
创建脚本文件并键入以下代码 -
f = x^3 - 2*x +5;
a = int(f, 1, 2)
display('Area: '), disp(double(a));MATLAB执行上述语句将返回以下结果 -
a =
23/4
Area:
5.7500以下是上面示例的Octave写法 -
pkg load symbolic
symbols
x = sym("x");
f = x^3 - 2*x +5;
c = [1, 0, -2, 5];
integral = polyint(c);
a = polyval(integral, 2) - polyval(integral, 1);
display('Area: '), disp(double(a));可以使用Octave提供的quad()函数给出一个替代求解代码,如下所示:
pkg load symbolic
symbols
x = sym("x");
f = inline("x^3 - 2*x +5");
[a, ierror, nfneval] = quad(f, 1, 2);
display('Area: '), disp(double(a));MATLAB执行上述语句将返回以下结果 -
Area:
5.7500示例2
查找曲线下面积:f(x)= x^2 cos(x),对于-4≤x≤9。
创建一个脚本文件并写下面的代码 -
f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp(‘Area: ‘), disp(double(a));
MATLAB
MATLAB执行上述语句将返回以下结果 -
同时也会输出以下内容 -
a =
8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9)
Area:
0.3326以下是上面示例的Octave写法 -
pkg load symbolic
symbols
x = sym("x");
f = inline("x^2*cos(x)");
ezplot(f, [-4,9])
print -deps graph.eps
[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));Matlab多项式
MATLAB表示多项式为包含由下降幂排列的系数的行向量。 例如,方程式
![]()
可以表示为 -
p = [1 7 0 -5 9];评估计算多项式
多值函数用于评估计算指定值的多项式。 例如,要评估前面的多项式p,在x = 4,可使用以下代码 -
p = [1 7 0 -5 9];
polyval(p,4)MATLAB执行上述语句返回以下结果 -
ans = 693MATLAB还提供polyvalm函数用于评估矩阵多项式。 矩阵多项式是以矩阵为变量的多项式。
例如,下面创建一个方阵X并评估求值多项式p,在X -
p = [1 7 0 -5 9];
X = [1 2 -3 4; 2 -5 6 3; 3 1 0 2; 5 -7 3 8];
polyvalm(p, X)MATLAB执行上述代码语句返回以下结果 -
ans =
2307 -1769 -939 4499
2314 -2376 -249 4695
2256 -1892 -549 4310
4570 -4532 -1062 9269计算多项式的根
roots函数计算多项式的根。 例如,要计算多项式p的根,可参考以下语法 -
p = [1 7 0 -5 9];
r = roots(p)MATLAB执行上述代码语句返回以下结果 -
r =
-6.8661 + 0.0000i
-1.4247 + 0.0000i
0.6454 + 0.7095i
0.6454 - 0.7095ipoly函数是roots函数的逆,并返回到多项式系数。 例如 -
p = [1 7 0 -5 9];
r = roots(p)
p2 = poly(r)MATLAB执行上述代码语句返回以下结果 -
Trial>> p = [1 7 0 -5 9];
r = roots(p)
p2 = poly(r)
r =
-6.8661 + 0.0000i
-1.4247 + 0.0000i
0.6454 + 0.7095i
0.6454 - 0.7095i
p2 =
1.0000 7.0000 0.0000 -5.0000 9.0000多项式曲线拟合
polyfit函数用来查找一个多项式的系数,它符合最小二乘法中的一组数据。 如果x和y包含要拟合到n度多项式的x和y数据的两个向量,则得到通过拟合数据的多项式,参考代码 -
p = polyfit(x,y,n)示例
创建脚本文件并键入以下代码 -
x = [1 2 3 4 5 6]; y = [5.5 43.1 128 290.7 498.4 978.67]; %data
p = polyfit(x,y,4) %get the polynomial
% Compute the values of the polyfit estimate over a finer range,
% and plot the estimate over the real data values for comparison:
x2 = 1:.1:6;
y2 = polyval(p,x2);
plot(x,y,'o',x2,y2)
grid onMATLAB执行上述代码语句返回以下结果 -
Trial>> x = [1 2 3 4 5 6]; y = [5.5 43.1 128 290.7 498.4 978.67]; %data
p = polyfit(x,y,4) %get the polynomial
% Compute the values of the polyfit estimate over a finer range,
% and plot the estimate over the real data values for comparison:
x2 = 1:.1:6;
y2 = polyval(p,x2);
plot(x,y,'o',x2,y2)
grid on
p =
4.1056 -47.9607 222.2598 -362.7453 191.1250同时还输出一个图形 -
Matlab转换
MATLAB提供了处理转换的命令,如拉普拉斯和傅里叶变换。转换在科学和工程中被用作简化分析和从另一个角度看待数据的工具。
例如,傅里叶(Fourier)转换允许我们将表示为时间的函数的信号转换为频率的函数。 拉普拉斯变换允许我们将微分方程转换为代数方程。
MATLAB提供了laplace,fourier和fft命令来处理拉普拉斯,傅立叶和快速傅里叶转换。
拉普拉斯变换
时间f(t)函数的拉普拉斯转换由以下积分 -
拉普拉斯变换也表示为f(t)到F(s)的变换。 可以看到此变换或集成过程将f(t),符号变量t的函数转换为另一个函数F(s)与另一个变量s。
拉普拉斯变换将微分方程转换为代数方程。要计算函数f(t)的拉普拉斯变换,参考以下代码 -
laplace(f(t))示例
在这个例子中,我们将计算一些常用函数的拉普拉斯变换。
创建脚本文件并键入以下代码 -
syms s t a b w
laplace(a)
laplace(t^2)
laplace(t^9)
laplace(exp(-b*t))
laplace(sin(w*t))
laplace(cos(w*t))MATLAB运行文件代码时,得到以下结果 -
Trial>> syms s t a b w
laplace(a)
laplace(t^2)
laplace(t^9)
laplace(exp(-b*t))
laplace(sin(w*t))
laplace(cos(w*t))
ans =
1/s^2
ans =
2/s^3
ans =
362880/s^10
ans =
1/(b + s)
ans =
w/(s^2 + w^2)
ans =
s/(s^2 + w^2)逆拉普拉斯变换
MATLAB中可使用命令ilaplace来计算逆拉普拉斯变换。
例如,
ilaplace(1/s^3)MATLAB执行上述代码语句得到以下结果 -
ans =
t^2/2示例
创建脚本文件并键入以下代码 -
syms s t a b w
ilaplace(1/s^7)
ilaplace(2/(w+s))
ilaplace(s/(s^2+4))
ilaplace(exp(-b*t))
ilaplace(w/(s^2 + w^2))
ilaplace(s/(s^2 + w^2))MATLAB执行上述代码语句得到以下结果 -
ans =
t^6/720
ans =
2*exp(-t*w)
ans =
cos(2*t)
ans =
ilaplace(exp(-b*t), t, x)
ans =
sin(t*w)
ans =
cos(t*w)傅里叶变换
傅里叶变换通常将时间f(t)的数学函数转换成有时由F表示的新函数,其参数是以周期/ s(赫兹)或每秒弧度为单位的频率。新功能被称为傅立叶变换和/或函数f的频谱。
示例
创建脚本文件并在其中键入以下代码 -
syms x
f = exp(-2*x^2); %our function
ezplot(f,[-2,2]) % plot of our function
FT = fourier(f) % Fourier transformMATLAB执行上述代码语句得到以下结果 -
同时也会输出以下结果 -
Trial>> syms x
f = exp(-2*x^2); %our function
ezplot(f,[-2,2]) % plot of our function
FT = fourier(f) % Fourier transform
FT =
(2^(1/2)*pi^(1/2)*exp(-w^2/8))/2绘制傅里叶变换为 -
syms x
f = exp(-2*x^2); %our function
% ezplot(f,[-2,2]) % plot of our function
FT = fourier(f) % Fourier transform
ezplot(FT)MATLAB执行上述代码语句得到以下结果 -
逆傅里叶变换
MATLAB提供了用于计算函数的逆傅里叶变换的ifourier命令。 例如,
f = ifourier(-2*exp(-abs(w)))MATLAB将执行上述语句并显示结果 -
f =
-2/(pi*(x^2 + 1))