检测模型中的边框回归(Bounding Box Regression)
1、为什么要边框回归?

对于上图,绿色的框表示Ground Truth,红色的框为Selective Search提取的Region Proposal。那么即便红色的框被分类器识别为飞机,但是由于红色的框定位不准(IoU<0.5),那么这张图相当于没有正确的检测出飞机。如果我们能对红色的框进行微调,那么经过微调后的窗口跟Ground Truth更接近,这样岂不是定位会更准确。确实,Bounding-box regression 就是用来微调这个窗口的。
2、边框回归是什么?
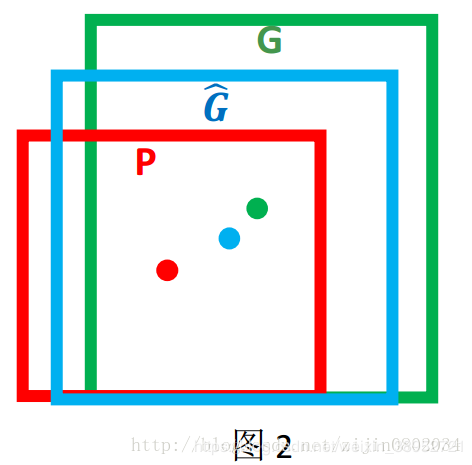
对于窗口一般使用四维向量 ( x , y , w , h ) (x,y,w,h) (x,y,w,h)来表示,分别表示矿口的中心点坐标和宽高。对于图2,红色框P代表原始的Proposal,绿色的框G代表目标的Ground Truth,我们的目标是寻找一种关系使得输入原始的窗口P经过映射得到一个跟真实窗口G更接近的回归窗口 G ^ \hat{G} G^。
边框回归即:给定 ( P x , P y , P w , P h ) \left ( P_{x},P_{y}, P_{w},P_{h}\right ) (Px,Py,Pw,Ph)寻找一种映射 f f f,使得 f ( P x , P y , P w , P h ) = ( G x ^ , G y ^ , G w ^ , G h ^ ) f \left ( P_{x},P_{y}, P_{w},P_{h}\right ) =\left ( \hat{G_{x}},\hat{G_{y}},\hat{G_{w}},\hat{G_{h}}\right ) f(Px,Py,Pw,Ph)=(Gx^,Gy^,Gw^,Gh^)并且 ( G x ^ G y ^ , G w ^ , G h ^ , ) ≈ ( G x , G y , G w , G h ) \left ( \hat{G_{x}} \hat{G_{y}},\hat{G_{w}},\hat{G_{h}},\right )\approx \left ( {G_{x}}, G_{y},G_{w},G_{h}\right ) (Gx^Gy^,Gw^,Gh^,)≈(Gx,Gy,Gw,Gh)
3、边框回归怎么做呢?
平移+尺度放缩
(1)对边框的中心位置进行平移 ( Δ x , Δ y ) \left ( \Delta x,\Delta y \right ) (Δx,Δy),则修正后的中心位置变为: G x ^ = P x + Δ x \hat{G_{x}}=P_{x}+\Delta x Gx^=Px+Δx G y ^ = P y + Δ y \hat{G_{y}}=P_{y}+\Delta y Gy^=Py+Δy
(2)对边框的宽高进行缩放 ( S w , S h ) \left ( S_{w} ,S_{h}\right ) (Sw,Sh),则修正后的边框的宽和高为: G w ^ = P w ∗ S w \hat{G_{w}}=P_{w}* S_{w} Gw^=Pw∗Sw G h ^ = P h ∗ S h \hat{G_{h}}=P_{h}* S_{h} Gh^=Ph∗Sh