IMU和GPS数据融合估计位置与速度(MATLAB实现)
简介
假设小车在一个方向上以 2cm/s2 的加速度运动了 100s,使用加速度计和GPS测量小车位置。GPS定位误差为高斯分布,方差为4m;加速度计的误差也为高斯分布,方差为0.01m/s2,并且由于加速度计放置不是完全水平的,有 0.03m/s2 的偏移。采用卡尔曼滤波,融合加速度计和GPS数据,估计小车的位置与速度。
1. 问题
如果只使用GPS数据估计,卡尔曼滤波器MATLAB实现(从一维到三维)一文给出了基本理论与测试效果。如果只使用加速度计数据,理论上系统是不可观的,也即不能稳定估计小车的速度[1],偏移误差将不断累积。
在小车运动中,已知加速度计数据和GPS定位数据,加速度计和GPS数据都有一定误差,如何融合数据,估算出小车的位置与速度?融合传感器数据真的能提高数据精确度吗?本文将作简单测试验证。
2. 卡尔曼滤波及参数
2.1 定义系统:
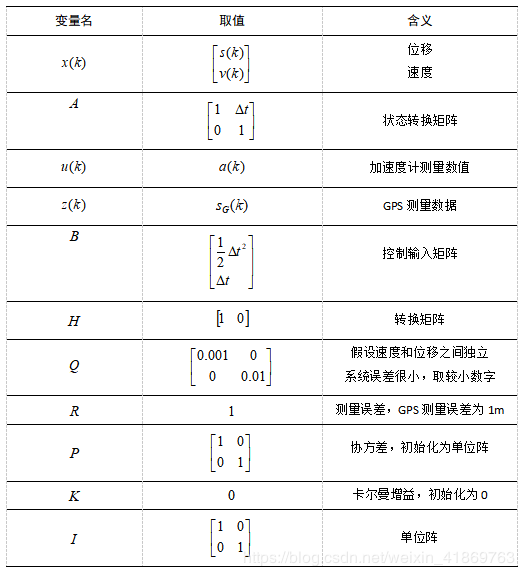
可见,在预测过程使用加速度计获取的数据,在滤波过程使用GPS数据。
3. 代码与效果
% ==================== 系统描述 ====================
% GPS精度为4m
% 加速度计的精度为 1cm/s^2,且有 3cm/s^2 的偏移
% 真实的加速度为 2cm/s^2
% 数据采集频率皆为 10Hz
% ================== 模拟产生数据 ==================
clear all
rng(0); % 设置随机数种子
dt = 0.1; % 0.1s采集一次数据
T = 0:dt:100; % 0~100s
N = length(T); % 采样点数
a = 2e-2; % 真实加速度
s = 1/2 * a * T.^2; % 真实位移(实际上不可知)
aa = a + 1e-2*randn(size(s)) + 3e-2; % 加速度计测量数据,有噪声,有偏移1
R = 4; % GPS 测量精度
z = s + sqrt(R)*randn(size(s)); % GPS 测量数据,开根号得到
% ================= 变量定义与初始化 =================
A = [1 dt; 0 1]; % 状态转移矩阵
H = [1 0]; % 转换矩阵
B = [1/2*dt^2; dt]; % 输入控制矩阵
Q = [0.001 0; 0 0.01]; % 过程噪声协方差,估计一个
P = eye(2); % 初始值为 1(可为非零任意数)
x = zeros(2, N); % 存储滤波后的数据,分别为位移、速度信息
k = 1; % 采样点计数
% ================= 卡尔曼滤波过程 ==================
for t = dt:dt:100
k = k + 1;
x(:,k) = A * x(:,k-1) + B*aa(k); % 卡尔曼公式1
P = A * P * A' + Q; % 卡尔曼公式2
K = P*H' * inv(H*P*H' + R); % 卡尔曼公式3
x(:,k) = x(:,k) + K * (z(:,k)-H*x(:,k)); % 卡尔曼公式4
P = (eye(2)-K*H) * P; % 卡尔曼公式5
end
% ==================== 结果绘图 =====================
figure(1);
plot(T, z(1,:),'b.');hold on; % GPS测量数据
plot(T, x(1,:),'r.'); % 滤波后数据
plot(T, s ,'k-'); % 绘制真实值
legend('滤波前','滤波后','理想值'); % 标注
xlabel('时间: s');
ylabel('距离: m');hold off;
axis([0 100 -20 120])
text(2, 110, ['滤波前方差: ' num2str(var(z - s))]) % 滤波前方差
text(2, 100, ['滤波后方差: ' num2str(var(x(1,:) - s))]) % 滤波后方差
figure(2);
plot(T(1:end-1), (x(1,2:end)-x(1,1:end-1))/dt, 'b.');hold on% 将滤波后位移差分结果
plot(T, x(2,:), 'r.'); % 滤波估计速度
plot(T, a*T, 'k-'); % 真实速度
legend('滤波位移差分','卡尔曼估计值','真实值')
xlabel('时间: s');
ylabel('速度: m');hold off;
axis([0 100 -8 10])
text(2, 9, ['位移差分方差: ' ...
num2str(var((x(1,2:end)-x(1,1:end-1))/dt - a*T(1:end-1)))]) % 滤波前方差
text(2, 7.6, ['速度滤波方差: ' ...
num2str(var(x(2,:) - a*T))]) % 滤波后方差
位移结果如下,滤波后方差变为原来 1/10.

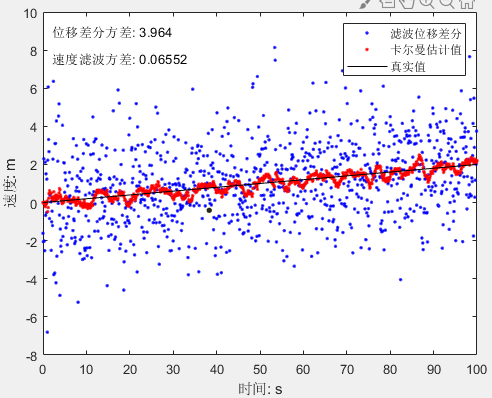
速度估计结果如下图。图中蓝色点为使用滤波后位移直接差分得到的结果,但是误差很大。其实,这样是不科学的,因为随着采样频率增加,单位时间内位移 dt 滤波的误差不会变化,但是 v=ds/dt,dt 随采样频率减小,误差会越大。而采用卡尔曼滤波的结果,误差较小。
4. 比较
只使用GPS数据或者加速度计的计算会如何呢?只使用GPS时,程序直接将矩阵 B 变为零矩阵即可。最终结果如下:
| 位移 | 速度 |
|---|---|
 |
 |
效果和GPS与IMU数据融合结果几乎没有差异。
只使用加速度计结果暂未写出,直观感受是有很大偏移。因为小车真实加速度为 2cm/s2,但是偏移量为3cm/s2,误差累加严重。
参考文献
[1]《多旋翼飞行器设计与控制》第八讲:可观性与卡尔尔曼滤波. 全权著.


