2019美赛B题PSO算法
本文参考网上算法学习PSO算法时,自己改变的一个例子
算法有PSO算法,还有自己变得一个可以求一组数中的第k个最大值的函数。
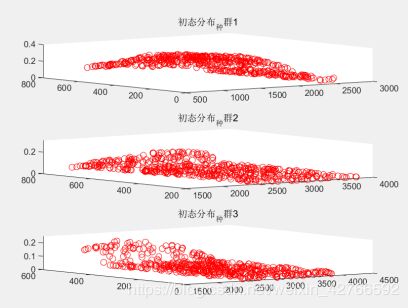
这是自己运行后的一个结果:
clear;clc;close all;
%% PSO
%选址:计算各个城市在扫描半径内的重要性
%% 参数输入
%城市
nc=520; %总城市
ncm=20;%药箱城市
ns=3; %选址个数
r=400; %扫描半径
d=0.8*r; %选点距离
da=d/2; %增加距离
lon=[20,40];
lat=[10,15];
longeur=(lon(2)-lon(1))*110; %km
large=(lat(2)-lat(1))*110; %km
r_route=10; %路长限制
%城市位置
xc(:,1)=longeur*rand(nc,1);
xc(:,2)=large*rand(nc,1);
%% 归一化自身重要性:GDP+药箱
level_self=50*rand(nc,1); %GDP
city_m=find( 100*rand(ncm,1)>=60 );%配有药箱城市
level_self(city_m)=floor(100*rand(length(city_m),1)); %药箱
level_self=level_self/sum(level_self);
%城市道路重要性
level_route=floor(rand(nc,1)*120);
level_route=level_route/sum(level_route);
%城市总重要性归一化
level_total=level_self+level_route;
level=level_total/sum(level_total);
%% 扫描半径内重要性计算: cas1 以城市为选址点的定态计算
p=level_read(xc,r,xc,level);
[cas11max,cas11nmax]=max(p);
[cas12max,cas12nmax]=maxn(p,2);
[cas13max,cas13nmax]=maxn(p,3);
cas1=[cas11max,xc(cas11nmax,1),xc(cas11nmax,2);cas12max,xc(cas12nmax,1),xc(cas12nmax,2);cas13max,xc(cas13nmax,1),xc(cas13nmax,2)];
figure(1);
%cas1输出
subplot(1,2,1);
plot(level,'b');
title('城市自身重要性');
xlabel('latitude/x');
ylabel('longitude/y');
zlabel('Level/z');
subplot(1,2,2);
plot(p,'r');
xlabel('latitude/x');
ylabel('longitude/y');
zlabel('Level/z');
title('城市总重要性');
%% 扫描半径内重要性计算:连续型计算
%PSO参数输入
N=500; %初始种群个数
np=ns; %种群数
d=2; %空间维数
ger=1000; %最大迭代次数
limit=[0,0;longeur,large]; %设置位置参数限制
vlimit=[-1,-1;1,1]; %设置速度限制
w=0.8; %惯性权重
c1=0.4; %自我学习因子
c2=0.6; %群体学习因子
x=zeros(N,d,np); %初始种群的位置
%% 寻找最优
%初始种群位置
x0(:,1)=longeur*rand(3,1);
x0(:,2)=large*rand(3,1);
for n=1:np
for k=1:d
x(:,k,n)=x0(n,k) + (limit(2,k) - limit(1,k)) * rand(N,1);
end
end
v=rand(N,d,np); %初始种群的速度
xm=x; %每个个体的历史最佳位置
%种群的历史最佳位置
ym(:,1)=longeur*rand(np,1);
ym(:,2)=large*rand(np,1);
fxm=zeros(N,np); %每个个体的历史最佳适应度
fym=repmat(-inf,np,1); %种群历史最佳适应度
%初态图
figure(2);
for k=1:np
subplot(3,1,k);
plot3(xm(:,1,k),xm(:,2,k),level_read(xm(:,:,k),r,xc,level),'ro');
title(['初态分布_种群',num2str(k)]);
end
%% 群体更新
record=zeros(3,ger); %记录器
fx=zeros(N,np);
distance=zeros(np,np);
xcn=zeros(np,2);
for iter=1:ger
%个体处理
for k=1:np
xcn(k,:)=mean(x(:,:,k));
end
%中心距离计算
for k=1:np
distance(k,:)= sqrt((xcn(k,1)-xcn(:,1)).^2+(xcn(k,2)-xcn(:,2)).^2);
end
%种群位置调整
for k=1:np
pop_n=find(0<distance(k,:)<d);
x(:,:,pop_n)=x(:,:,pop_n)+da;
end
%计算每个种群的最大值
for npk=1:np
fx(:,npk)=level_read(x(:,:,npk),r,xc,level); %个体当前适应度
for i=1:N
if fxm(i,npk)<fx(i,npk)
fxm(i,npk)=fx(i,npk); %更新个体历史最佳适应度
xm(i,:,npk)=x(i,:,npk); %更新个体历史最佳位置
end
end
%种群处理
[fym(npk),nmax]=max(fxm(:,npk)); %更新群体历史最佳适应度
ym(npk,:)=xm(nmax,:,npk); %更新群体历史最佳位置
% 速度更新
v(:,:,npk)= w*v(:,:,npk) + c1*rand*(xm(:,:,npk)-x(:,:,npk)) + c2*rand*(repmat(ym(npk,:),N,1)-x(:,:,npk));
% 边界速度处理
for k=1:d
vv=v(:,k,npk);
vv(vv<vlimit(1,d)) = vlimit(1,d);
vv(vv>vlimit(2,d)) = vlimit(2,d);
v(:,k,npk)=vv;
end
x(:,:,npk)=x(:,:,npk)+v(:,:,npk);% 位置更新
% 边界位置处理
for k=1:d
xx=x(:,k,npk);
xx(xx<limit(1,d)) = limit(1,d);
xx(xx>limit(2,d)) = limit(2,d);
x(:,k,npk)=xx;
end
end
record(:,iter)=fym; %最大值记录
end
cas2=[fym,ym];
%% 输出动态结果
figure(3);
for n=1:np
subplot(3,1,n);
plot(record(n,:),'r');
title(['收敛过程',num2str(n)]);
xlabel('代数');
ylabel('Level');
end
disp(cas1(:,1)');
disp(cas1(:,[2 3])');
disp(cas2(:,1)');
disp(cas2(:,[2 3])');
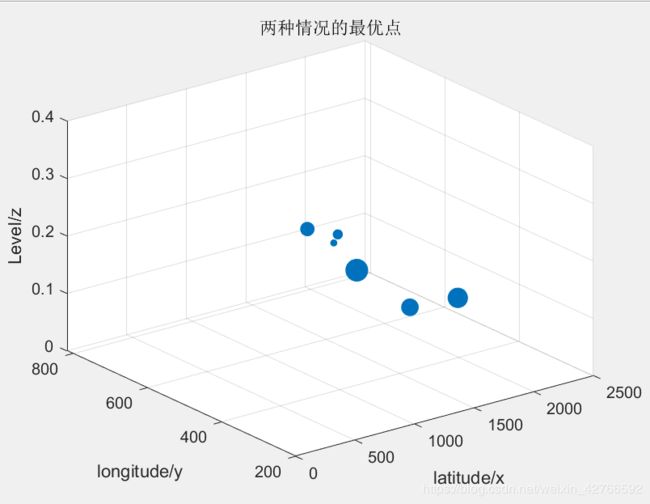
figure(4)
s=[80 40 20 200 160 120];
cas=[cas1;cas2];
sx=cas(:,2)';sy=cas(:,3)';sz=cas(:,1)';
scatter3(sx,sy,sz,s,'filled');
xlabel('latitude/x');
ylabel('longitude/y');
zlabel('Level/z');
title('两种情况的最优点');
function level_r=level_read(x,r,xc,level)
%% 重要性读取函数 level_r=level_read(x,level)
%x(long,large):计算位置矩阵 r:扫描半径 xc:城市位置 level:重要性 level_r:计算重要性
level_r=zeros(size(x,1),1); %记录器
for n=1:size(x,1)
xx=x(n,:);
for k=1:length(level)
rr=sqrt( sum( (xx-xc(k,:)).^2 ) ); %计算比较半径
if rr<=r
level_r(n,1)=level_r(n,1)+level(k);
end
end
end
end
function [maxnn,nmax]=maxn(x,n)
%% 提取d第n个最大值
%x:数组 maxn:第n个最大值 nmax:nmax的位置
xx=x; %数组转存
for k=1:n
maxnn=max(xx);
xx((xx>=maxnn))=[]; %去除第k个最大值
end
mut=find(maxnn==x);
nmax=mut(1);
end

