能用三角函数表示声音吗——正弦模型综述

摘要：正弦模型(Sinusoidal Modeling)指的是用一系列振幅、频率和相位不断变化的正弦波来拟合音频。其有非常丰富的应用场合。相比于非常成熟的线性预测模型(Linear Prediction)，中文技术社区对于正弦模型的介绍并不足够。本文参考了十余篇英文文献，阐述这一模型的思想和实现思路，解释其中的技术细节。

---

本文由@EthanLifeGreat/@EthanUnbeaten原创发表于CSDN

1.前言

模型的目的在于用相对熟悉的属性来描绘未知的事物。而将音频看作是不同的正弦信号的叠加是一个看起来比较自然的想法（其中存在的不合理之处将会在后面提及）。

如果能够实现，那么建模者对于音频的整体属性就能形成直观的理解，同时有利于对音频进行想要的调整。

在介绍模型之前，请允许笔者先对相关概念进行简单介绍。

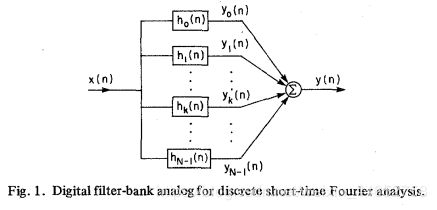
1.1.声码器(The Digital Phase Vocoder)

用正弦波来拟合声波的办法最早在70年代由Moor提出¹。后来经过完善，发展出了声码器²。

声码器将声音信号与多个滤波器相卷积（其本质是离散傅里叶变换）得到多个频率的子带(subband / DFT bin)，以及子带上的振幅和相位。

后来发明的MPEG音频编码方式也是基于这个思想——对不同的子带分配不同比特（信息计量单位）。清晰记录音频中人耳敏感的部分；模糊记录不敏感的部分。

尽管声码器的实践和正弦模型的实践方式接近，其本质的思维方式是不同的。DPV注重于固定频率通道(channel)的内容，没法沟通相邻的频率通道，故对刻画跨通道变化的频率并不完美。

对此，Smith等人³和McAulay等人⁴独立地提出峰值跟踪(Peak Tracking)的解决方案，正式地将正弦波的概念引进模型。这将是本文讨论的重点。

---

2. 分析(Analysis)

2.1. 短时傅里叶变换(STFT)

如前面所言，需要用正弦波来表示音频信号，必须找到正弦波们的频率、对应的振幅和对应的相位。对此，我们需要的频率分析工具是傅里叶变换(Fourier Transform, FT)，具体而言，是离散傅里叶变换(DFT)。后者是前者在计算机上的版本。

然而仅仅进行一次DFT是不足够的，我们首先需要对音频在时间上进行分帧(frame)，对每一帧独立地进行DFT，这被称为短时傅里叶变换(STFT)/离散短时傅里叶变换(DSTFT). 这么做的原因在于：我们希望在每一个帧里，具有平稳性——例如（在语音分析里）最多存在一个音素(phone). 夸张地讲，如果含有两个字的音频片段被同时送入DFT进行分析，我们便难以分析字的内容，也难以辨别两个字的先后顺序。

由于稳定性的影响，我们需要让每一帧尽可能短。然而对于DFT而言，过短的信号意味着更少的信息，将会使频谱的分辨率下降，使得我们难以区分频率相近的成分。其中，FT的时间分辨率和频率分辨率满足反比例关系：分析帧时间越短(时间分辨率高)，则频率分辨度越低；反之亦然。这被称为Gabor极限(Gabor–Heisenberg Limit)⁵.

因此，对帧率（每秒分割的帧数）的选择也是STFT的一门艺术。新竹清华大学的劉奕汶教授⁶对此有一句总结：“（窗长）尽量长，不能太长。”

其中的窗长等于帧长，由于截取分析帧后通常要加分析窗，而分析窗的长度与帧长相等。对于分析窗的介绍，可以参考Harris的文章⁷. 对此我之前的 文章 也有简要论述。

更详尽地了解STFT，或可参见Matlab官方封装的函数 stft.m . 受篇幅限制，本文不再赘述。

2.1.1.零延拓(Zero-padding)

进行离散傅里叶变换前，为了提高变换后的频率分辨率——即更接近的DTFT的连续的结果——我们需要对加窗后的信号进行零延拓，即在信号后面补零。

由于FFT的运算性质，一般将补零后的长度为2的某次方（视情况而定，如1024，4096等）。

另外，为了使得相位一致，应使加窗信号居于DFT输入的正中间（x取0处），其余部分为补足的零。如下图（图源⁸）：

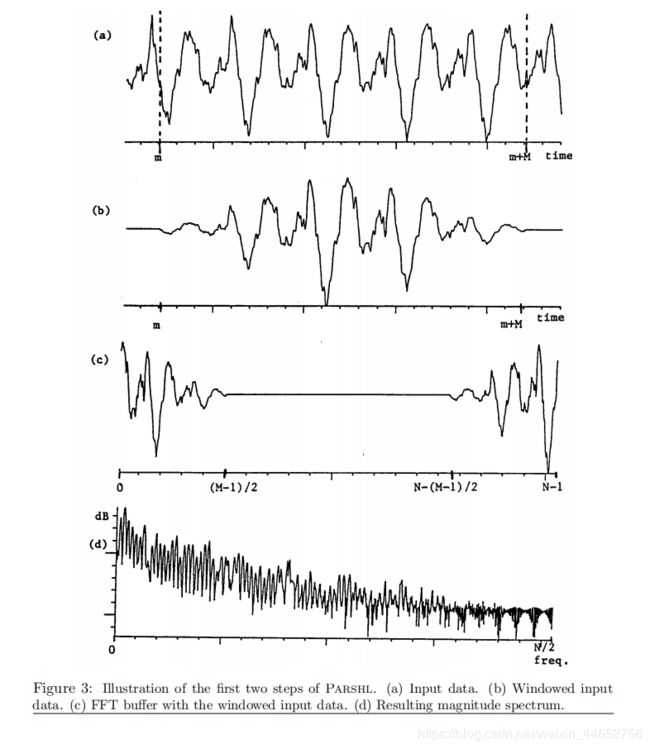
从上至下以次为：(a)原信号 (b)加窗信号 (c)延拓信号 (d)信号频谱。

2.2.峰值检测与估计(Peak Detection and Estimation)

对帧内容进行N点DFT/FFT后，可以得到一个自变量为频率的离散的复值函数。函数值的绝对值为频率处对应振幅，虚部与实部之比的反正切值为相角。

峰值指的是对于振幅谱上的极大值点。

一般认为，只有较大的峰值才是频谱中有价值的内容。而那些较最大峰值低80dB以上的峰值，将难以被听到且其分辨率很低⁹。对存在这些峰值的音频分析结果进行调整（如变调）可能带来音频质量下降。

同时，某些峰值可能并非真正存在于原本的音频内容中，而是源于离散傅里叶变换过程。例如一个被正弦窗截断的正弦波，经过DFT后会出现许多的峰值：

因此，峰值检测的流程并不仅仅包括找到极大值点，还在于对找到的极大值点进行筛选，即：

• 删掉不重要的极大值点
• 删掉本身不存在于音频中的峰值等

一个峰值检测的结果例子如下图，叉为峰值（图源⁹）：

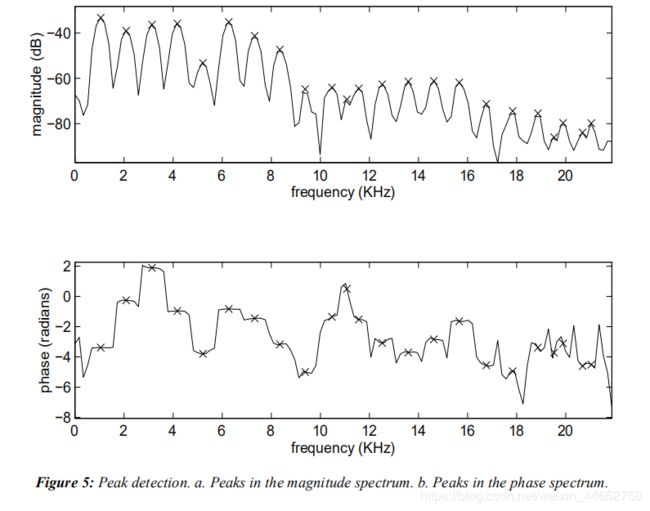
然而如第一段所言，尽管此函数在图上看起来连续，但其仍是离散函数，要高效地找到隐藏的极大值点（即峰值估计），可以使用插值法(interpolation).

2.2.1. 二次曲线/抛物线插值(Quadratic/Parabolic Interpolation)

在对数谱上取振幅最值点附近三点，进行二次曲线/抛物线插值(Quadratic/Parabolic Interpolation)，得到估计出的最值点¹⁰，再据此对相位进行线性拟合。二次插值示意图如下（图源新竹清华大学课件⁶）：

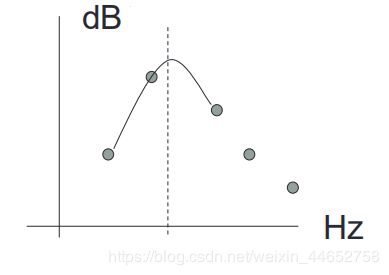
注意插值进行的纵坐标是分贝dB（对数谱），经验证明，在对数谱上进行二次插值的精确度比在线性谱上的精确率高一倍⁸。

另外，除了使用DFT分析出频率成分，还有学者使用最优化的思想，迭代计算出音频中主要成分的振幅、频率和相位，这被称为“使用合成来分析”¹¹(Analysis-by-synthesis, ABS)¹²。

2.3. 音高检测(Pitch Detection)

找到了峰值之后，我们可以选择进行音高检测。这可以对之后的分析带来某些方便。

在此之前我们需要先介绍一些音乐方面的概念。

音高(Pitch)的是音乐领域里比较模糊的一个概念，笔者比较认同的一个解释是——听感上最相近的纯音的频率（a percept that can be compared against that of a pure tone）⁶。

音高通常被直观地定义为基频(Fundamental Frequency)，基频可以被定义为泛音/谐波(partial/harmonic)序列里的公因数。例如，钢琴键C4的基频是261.6Hz，但其频谱成分却包含许多（近似于¹³）261.6的倍数的成分，如下（图源¹⁴）：

基于以上知识，我们不难想象检测音高（基频）的算法设计过程。但是，音高检测又有什么好处呢？

• 判断噪音。如果某个峰值离基频的任何倍数都较远，那么这个峰值很可能不属于这个音。
• 改善分析窗的长度。知道了某个帧中的音的音高，便可以设置合适的分析窗长度，以获得更好的时间-频率效益取舍⁹。这种分析法也被称为“音高-同步分析”¹¹(Pitch-synchronous Analysis).
• 便于调整音高。如果对音频音高进行调整时直接将所有的频率成分乘以某一倍数，则会放大谐波与基频倍数之间的差距¹³，使得改变后音频变得更加不和谐¹²。

2.4. 峰值连接(Peak Continuation/Peak Matching)

峰值连接的本质是把相邻帧内的峰值相连，更确切地说是将相邻帧内对应频率的峰值相连，因此也被称为峰值匹配(matching). 而对应频率一般意味着彼此在各自帧内的频率最接近。

这么做的理论基础在于，我们确信一个稳定的声音由多个频率近似稳定，而振幅不断变化的成分构成。那么，为了得到对声音的更连续的描述，我们可以基于这个假设，对相邻帧内的峰值内插，也相当于去掉了“帧”这个离散的存在。以下是连接的示意图（图源¹⁵）：

其操作大致流程是，为帧内的每一个峰值在下一个帧内找一个最相近的峰值。在满足相连接的峰值频率差小于一个给定值的前提下，对产生的冲突（多连一、一连多）按照一定规则进行解决。如果一个峰值在下一个帧找不到对应的连接，则被视为是一个轨道(track/trajectory)的死亡(death)；而如果一个峰值没有被前一个帧中的峰值对应，则被视为是一个轨道的诞生(birth)。

关于峰值连接中类似的概念表述有许多，其最终功能近似，不一一列举。

2.5. “正弦+噪声+暂态”模型(Sinusoidal+Noise+Transient)

本节简要解决一下音频中正弦波不能很好拟合的部分。

前面提到，正弦波只适合于拟合一个稳定的声音（如乐音）。而对于噪声（如雨声）或者暂态声音（如打击音/Attack）都没办法很好地拟合。

例如，以下是一段人声的峰值连接结果（图源¹⁵）：

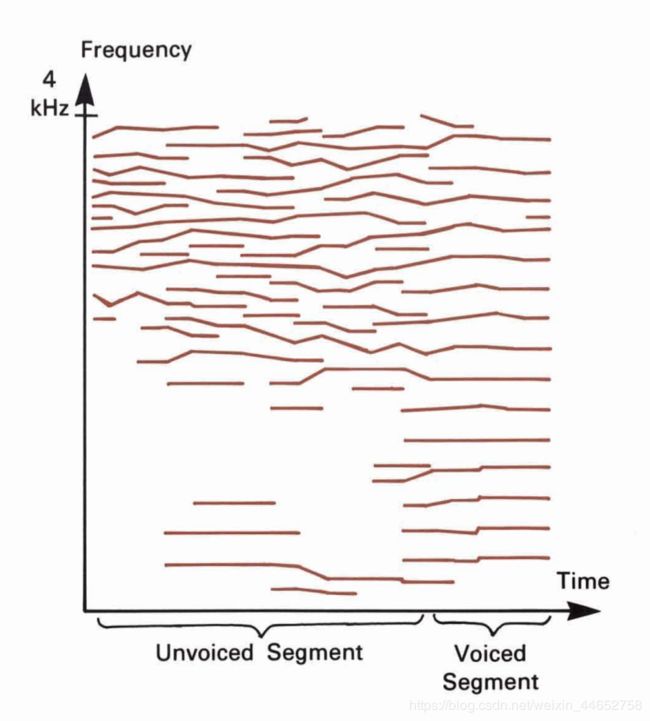
其中的清音部分(Unvoiced Segment)峰值多、轨道短，这样模型拟合效率低、效果差。而相比下浊音部分(Voiced Segment)显得合适很多。

2.5.1. “正弦+噪声”模型(Sinusoidal+Noise)

了解过语音识别的同学可能知道，清音其实就近似于噪音。于是，我们有了“正弦+噪声”模型，或叫“决定+随机”模型(Deterministic+Stochastic)¹⁶。

它首先拟合出正弦波成分，又叫确定性(Determinisitic)成分，剩下的部分称为剩余(Residual)。

对于正弦波拟合不好的剩余，该模型视其为在不同频率部分能量不同的噪声¹⁷。我们只记录其大致位置的振幅，也就是描绘出它频谱的包络，如下图b子图中的折线（图源⁹）。

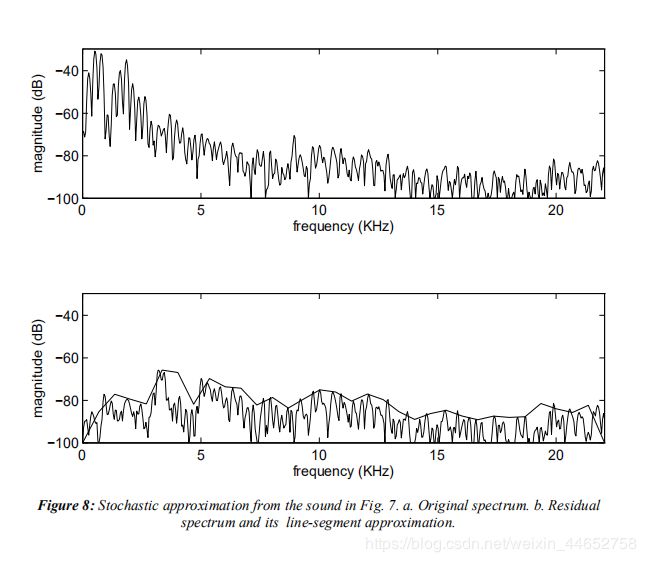
这种做法会模糊频率的精度，同时丢失相位信息，但好处是可以用较少的数据量表示正弦波无法拟合的噪声。

2.5.2. 暂态模型(Transient Model)

暂态主要指敲击瞬间发出的声音，即ADSR包络中的（时间很短的）Attack。

这一部分无法很好地用正弦波或噪声的办法拟合¹⁸。有一种解决办法是先把暂态时间段剥离出来，不对之进行分析，等合成的时候直接给拼回来¹⁹。

Verma等人¹⁸则认为这种做法不符合正弦模型的“变通精神”(the flexible spirit)，同时这种在时域上剥离暂态也会带走某些噪声。因此，他们提出了对暂态建模的办法。

Verma等人的做法是，对暂态部分先进行离散余弦变换(Discrete Cosine Transform, DCT)²⁰，定义如下：
$$C[k]=\beta [k]\cdot x[n]\cdot cos[\frac{(2n+1)k\pi }{2N}]$$
其中 $k=1$ 时 $\beta [k]=\sqrt{\frac{1}{N}}$，否则 $\beta [k]=\sqrt{\frac{2}{N}}$.

简单而言，DCT可以将冲激信号转换为余弦函数。进而便于进行正弦拟合。如，一个指数速度衰减的信号和其经DCT变换后形式如：

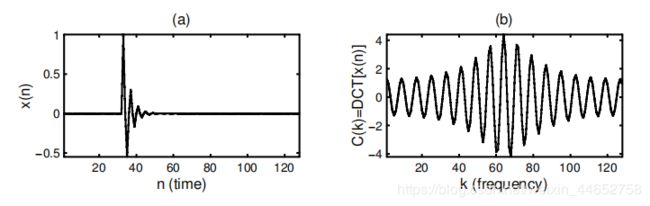
暂态模型分析/合成流程如下：

与“正弦+噪声”模型相结合时，可以按暂态、正弦、噪声的顺序，也可以按正弦、暂态、噪声的顺序进行分析。

其实写完这一节才发现有许多的暂态模型，可以参考斯坦福大学CCRMA²¹的网页了解更多

---

3. 合成(Synthesis)

合成的意思是用分析得到的参数化表示，合成出近似于原来的 或 任何想要的音频。

为了印证“声音能用三角函数来表示”，我们当然需要用正余弦波来合成信号。所使用的正余弦波参数（频率、振幅和相位）就是我们在分析中得到的数据。

在此，我们主要探讨正弦部分的合成（即不讨论2.5.中的“噪声”和“暂态”部分）。介绍三种合成办法，它们分别是：“仅振幅合成法”¹¹(Magnitude-Only Synthesis)、相位内插合成法(Phase Interpolation Synthesis)和帧重叠相加法(Overlap-Add Synthesis)。

3.1. “仅振幅合成法”(Magnitude-Only Synthesis)

顾名思义，这个办法仅使用分析得到的频率和对应的振幅（不用相位）进行合成。

这个办法（相较于相位内插）可以大大简化合成的流程，理解起来也比较直观——

比如做实验的时候，我们想生成一个频率为f的正弦波，我们一般会忽略相位：

t = linspace(0,1,44100);		% 时间线(s)
A = 1;							% 振幅
f = 1000;						% 频率(Hz)
signal = A*sin(2*pi*f.*t);		% 频率1000Hz，相位为0的正弦波

但其实相位(0)隐藏在了里面。

在许多场合下，人耳对于相位是不敏感的，例如你基本没法用耳朵区分这两个信号：

signal1 = A*sin(2*pi*f.*t)
signal2 = A*cos(2*pi*f.*t)

这就赋予了只用振幅合成法的现实意义。

“仅振幅合成”的具体的操作办法是：对于2.4.中连接好的每一条轨迹，设其初始相位为0（或者其它某值，效果相同），逐采样点迭代相位并内插振幅后，取各点正弦值，最后按时间顺序将所有轨迹的正弦值对应相加。 其表达式为：

$$\sum _{所有轨迹j}{A}_j[n]\cdot cos({\varphi }_{j,n})$$
其中，（省略 $j$）
$${\varphi }_n={\varphi }_{n-1}+\frac{2\pi }{f_s}\cdot f[n]$$
其中，n表示时域顺序，即n=0表示该轨迹的起点，${\varphi }_0$=0，$f_s$表示采样频率（下同）.

A[n]与f[n]是由分析结果（A[m]与f[m]）线性内插而来的振幅和频率序列，满足：
$$A[n]=A[m]+\frac{A[m+1]-A[m]}{\Delta t\cdot f_s}\cdot n$$
$$f[n]=f[m]+\frac{f[m+1]-f[m]}{\Delta t\cdot f_s}\cdot n$$
这两条等式非常直观，就是直线的两点式，其中$\Delta t$为相邻分析帧的中心位置时间差。

关于不考虑相位的弊端和适用场合的讨论将放在下一节进行。

3.2. 相位内插合成法(Phase Interpolation Synthesis)

这节我们讨论考虑相位的合成办法。

考虑相位的合成法需要将相位也进行内插，即确定帧与帧间各点的相位信息。

3.2.1. 三次多项式内插法(Cubic Polynomial Interpolation)⁴

不同于振幅内插和3.1.中的频率内插的线性办法，相位内插所使用的内插办法是三次方(cubic)的。

为什么是三次？首先我们讲讲为什么不能是线性（一次）或二次的。这是因为：

• 频率是相位的导数，要保证相位曲线在两端的导数值是对应的频率。
• 分析时得到的相位只是对 $2\pi$ 取模的结果，在 $[-\pi ,\pi ]$ 间。

这时我们需要对相位进行加 $M\cdot 2\pi$ 展开(unwrap)，M 为某待定整数。再用其它先验知识来求出最合适的M。

例如⁴文中的图6，展示了五种可能 M 带来的内插结果：

如何从中选择最合适的M呢？作者McAulay等人提出的办法是，找一个“最平滑的”(maximally smooth)曲线，也就是曲线的二次导数的平方的线积分最小。即求整数M，使得

$$f(M)={\int }_0^T[{\theta }^{\prime \prime }(t;M){]}^{2}dt$$
最小。

得到相位后取余弦，点乘线性内插后的振幅即可，再把所有轨迹相加即可：⁴

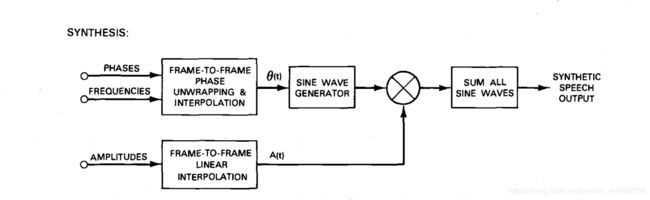
3.2.2 相位的意义

尽管我们听不出正弦波和余弦波的差别，在许多的情况下，人对于相位是敏感的，这些情况是：

• 对象分析过程不当⁹
• 非常低沉的乐器声音(低于30Hz⁹，低于100Hz⁴)
• 某些人声(含有较高的泛音)⁹
• 含有噪音的语音片段(会导致合成的噪音部分有一种不真实和令人厌烦的音效)⁴

一个大提琴波形、带相位和不带相位合成的结果对比图如下：¹⁶

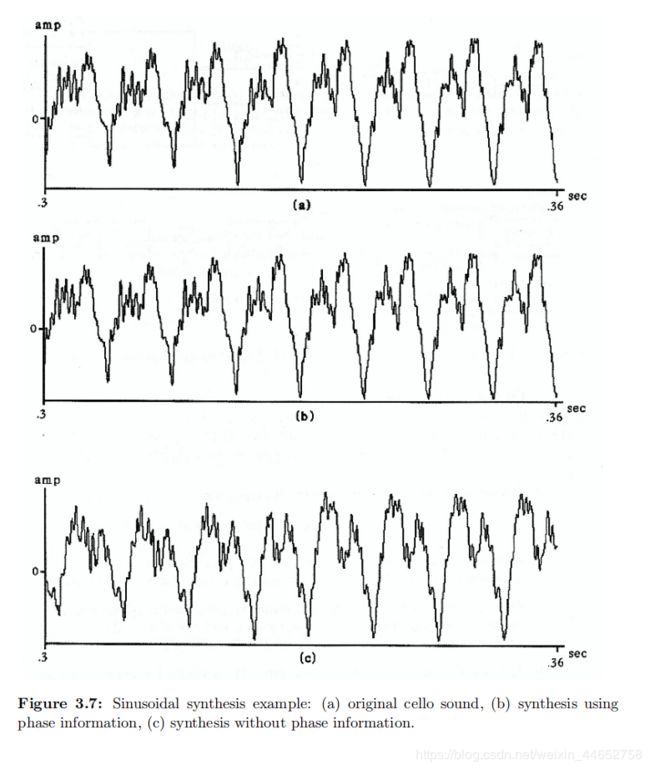
可以看出带相位的合成法基本保持了原来的波形（而且几乎完美复刻），反观不带相位的就不知道是哪跟哪了（虽然听起来可能差不多）。

3.3. 帧重叠相加法(Overlap-Add/OLA Synthesis)

这种办法事实上并没有进行峰值连接，它只是单纯地把每一帧的内容合成出来，再按一定规则拼加在一起。其中叠加的意义在于使帧和帧之间过度自然。

每个帧内的每个峰值对应一段正弦波，其振幅、频率恒定，相位由中心相位和频率共同决定，也是用频率逐点迭代。

方便起见，这里直接写代码了，毕竟够短。

leftHalf = floor(N/2);	  % N是帧内的采样点数
startPha = pha - (leftHalf+1)*freq;	% pha是分析得到的相位，freq是分析得到的频率，均视作中心相位、频率。
phas = startPha + freq.*(1:N);
y = sum(amp.*cos(phas), 1);       % 所有正弦波相加

合成好了帧内的内容便可以进行叠加了。叠加前要进行加窗，这里要保证窗叠加的结果是常数，这被称为常数叠加(Constant Overlap-Add, COLA).

关于COLA，中文社区里已经有很多介绍了，不再赘述。

4. 结语

本文主要介绍了Sinusoidal Modeling的分析、合成过程。讨论了实践中的一些细节。

关于本文的编程实现，可以参考笔者的Gitee项目基于Matlab的正弦模型项目。到底能不能用三角函数表示声音？运行代码听听区别就知道啦。

下一篇文章我们将讨论正弦模型的一些实际应用场合。

欢迎读者就文章及相关内容留言探讨。

---

注脚

---

1. Moorer, J. A. 1973. “The Hetrodyne Filter as a Tool for Analysis of Transient Waveforms.” MemoAIM-208, Stanford Artificial Intelligence Laboratory, Computer Science Dept., Stanford University. ↩︎

2. Portnoff, M.R. 1976. “Implementation of the Digital Phase Vocoder Using the Fast Fourier
   Transform.” IEEE Transactions on Acoustics, Speech and Signal Processing 24(3):243–248. ↩︎

3. Smith, J.O. and X. Serra. 1987. “PARSHL: An Analysis/Synthesis Program for Non-HarmonicSounds based on a Sinusoidal Representation.” Proceedings of the 1987 International Computer Music Conference. San Francisco: Computer Music Association. ↩︎

4. McAulay, R.J. and T.F. Quatieri. 1986. “Speech Analysis/Synthesis based on a Sinusoidal Representation.” IEEE Transactions on Acoustics, Speech and Signal Processing 34(4):744–754. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎

5. GABOR, D. Acoustical Quanta and the Theory of Hearing. Nature 159, 591–594 (1947). https://doi.org/10.1038/159591a0 ↩︎

6. http://ocw.nthu.edu.tw/ocw/index.php?page=course&cid=130& ↩︎ ↩︎ ↩︎

7. F.J. Harris, On the use of windows for harmonic analysis with the discrete Fourier transform, Proc. IEEE 66 (1) (1978) 51–83. ↩︎

8. Smith, Julius & Serra, Xavier. (2005). PARSHL: An Analysis/Synthesis Program for Non-Harmonic Sounds Based on a Sinusoidal Representation. Proceedings of the International Computer Music Conference. ↩︎ ↩︎

9. Serra, X. . Musical Sound Modeling with Sinusoids plus Noise. Musical Signal Processing. 1997. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎

10. M. Abe and J. Smith, “Design criteria for simple sinusoidal parameter estimation based on quadratic interpolation of FFT magnitude peaks”, (AES 2004) ↩︎

11. 未找到对应中文译名，笔者译。 ↩︎ ↩︎ ↩︎

12. George, E. Bryan, Smith, Mark J. T. An Analysis-by-Synthesis Approach to Sinusoidal Modeling Applied to the Analysis and Synthesis of Musical Tones[J]. journal of the audio engineering society, 1991. ↩︎ ↩︎

13. 声音的泛音/谐波频率通常并非基频的完美倍数。例如本文图6中，钢琴C4音的频谱的前五个谐波的频率比是1.0000 : 2.0000 : 3.0033 : 4.0075 : 5.0163¹⁴。导致这种非整数的原因是琴弦僵硬的弯折²²。 ↩︎ ↩︎

14. Szeto, Wai Man , and K. H. Wong . “Sinusoidal modeling for piano tones.” Signal Processing, Communication and Computing (ICSPCC), 2013 IEEE International Conference on IEEE, 2013. ↩︎ ↩︎

15. McAulay, R. J., & Quatieri, T. F. (1988). Speech Processing Based on a Sinusoidal Model. The Lincoln Laboratory Journal, 1(2), 153–168. ↩︎ ↩︎

16. Serra, X. 1989. “A System for Sound Analysis/Transformation/Synthesis Based on a Deterministic Plus Stochastic Decomposition.” PhD thesis, Stanford University. ↩︎ ↩︎

17. 注：如果一个噪声在所有频率成分上能量都相等，则是白噪声(white noise)；否则为有色噪声。相关内容参见百科词条“有色噪声”。 ↩︎

18. Verma, T. S. , & Meng, T. H. Y. . (2000). Extending spectral modeling synthesis with transient modeling synthesis. Computer Music Journal, 24(2), 47-59. ↩︎ ↩︎

19. Scott Nathan. Levine, Smith, & Julius Orion. (1998). Audio representations for data compression and compressed domain processing /. ↩︎

20. Rao, Kamisetty & Yip, P… (1990). Discrete cosine transform. Algorithms, advantages, applications. ↩︎

21. https://ccrma.stanford.edu/ ↩︎

22. A. Askenfelt, Ed., Five Lectures on the Accoutics of the Piano. Royal Swedish Academy of Music, 1990, available online at http://www.speech.kth.se/music/5_lectures/. ↩︎