AI-语音处理理论和应用-HMM
学习目标
• 了解语音处理的基础知识及应用
• 掌握语音处理的基本步骤
• 掌握语音处理的主要技术
• 了解语音处理的难点与展望
HMM
马尔科夫链
• 某同类商品A,B,C的宣传力度不同,顾客在广告宣传的效应下第一次尝试选择购买商品A,B,C的概率分别是0.2,0.4,0.4。顾客的购买倾向为下表,求某顾客第4购买各商品的概率。

• 三要素:
• 初始概率:π=(0.2,0.4,0.4)
• 转移概率:p_AA=0.8,p_AB=0.1, p_AC=0.1, p_BA=0.5,……
• 转移概率矩阵:
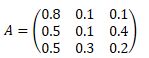
• 求解:
• 马尔科夫链模型:
• P(X_(n+1)=x│X_1=x_1,X_2=x_2,…,X_n=x_n )=P(X_(n+1)=x|X_n=x_n)
• 第三次概率: P_AAA= ?
• 马尔可夫链,是指数学中具有马尔可夫性质的离散时间随机过程。该过程中,在给定当前知识或信息的情况下,过去对于预测将来是无关的,只与当前状态有关。
• 在马尔可夫链的每一步,系统根据概率分布,可以从一个状态变到另一个状态,也可以保持当前状态。状态的改变叫做转移,与不同的状态改变相关的概率叫做转移概率。
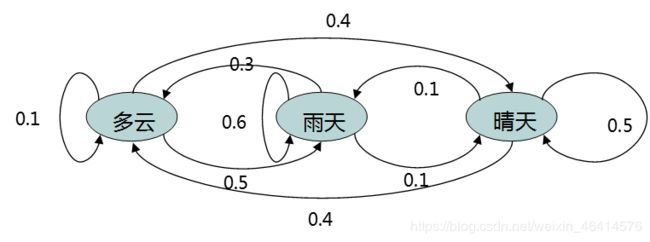
• 原理:
• 马尔可夫链描述了一种状态序列,其每个状态值取决于前面有限个状态。马尔可夫链是具有马尔可夫性质的随机变量的一个数列。这些变量的范围,即它们所有可能取值的集合,被称为“状态空间”。
• 性质:
• 正定性:状态转移矩阵中的每一个元素被称为状态转移概率,由概率论知识可知,每个状态转移概率皆为正数,公式可表示为:p_ij (k)≥0
• 有限性:根据概率论知识,状态转移矩阵中的每一行相加皆为1,用公式可表示为:∑▒p_ij =1
可观测马尔科夫模型
• 对弈一个问题而言,我们有初始分布π,转移概率矩阵A,在给定的任意一个时刻t,我们都有一个状态Q_t;一个状态随着时间的变化转移到另一个状态,由此便能得到一个观测序列,即为状态序列O=[q_1,q_2,q_3,q_4,…,q_n]。且整个问题中总共有n个观察状态。
• 出现这样的序列的概率为:
P ( O ∣ A , π ) = P ( q 1 ) ∏ t = 2 m P ( q t ∣ q t − 1 ) P\left ( O\mid A,\pi \right )=P(q_{1})\prod_{t=2}^{m}P(q_{t}\mid q_{t-1}) P(O∣A,π)=P(q1)t=2∏mP(qt∣qt−1)
• 所以一个可观测的马尔科夫模型由一个三元组描述: (A,π,n),一般情况下可以简写为:(A,π)。
穷举法
• 如果我们穷举了所有的观测序列……
• π_i=以状态i开始的序列的数目/序列总数
• p_ij=从状态i转移到状态j的序列的数目/从状态i序列总数
• [红,红,红][红,红,蓝][红,蓝,红][蓝,红,红]
• π={0.75,0.25}
• p_红蓝=1/3〖, p〗红红 〖=2/3,p〗蓝蓝=0,p_蓝红=1
隐马尔科夫模型
• 隐马尔可夫模型(Hidden Markov Model,HMM)是马尔可夫链的一种,它的状态不能直接观察到,但能通过观测向量序列观察到,每个观测向量都是通过某些概率密度分布表现为各种状态,每一个观测向量是由一个具有相应概率密度分布的状态序列产生。所以,隐马尔可夫模型是一个双重随机过程----具有一定状态数的隐马尔可夫链和显示随机函数集。
• HMM可以用5个元素来描述:
• 观测集合:R={R_1 〖,R〗2,R(3,…,) R_m }
• 观测序列:O={o_1 〖,o〗2,o(3,…,) o_l }
• 状态集合:S={S_1 〖,S〗2,S(3,…,) S_n }
• 状态序列:Q={q_1 〖,q〗2,q(3,…,) q_l }
• 观测概率:P{o_j=R_k ├|q_t=S_j ┤}=b_j (i),记B=[b_j (i)]
• 所以,HMM可以由一个五元组描述λ=(A,B,π,R,S),也可简写为λ=(A,B,π,)。
• 隐马尔可夫模型实际上是标准马尔科夫模型的扩展,添加了可观测状态集合和这些状态与隐含状态之间的概率关系。
HMM三个主要问题
• 评价问题:给定了马尔科夫模型后,去计算观测序列出现的可能性
• 前向算法
• 所谓评价问题便是去计算HMM关于某一特定观测序列的似然比 (likelihood),具体来说便是:给定一个HMM模型,参数为λ=(A,B)和一个观测序列O=o_1 o_2…o_T,计算观测序列的似然比P(O│λ)。
• 算法步骤:
• 初始化:α_1 (j)=α_0j×b_j (o_1 ) (其中1≤j≤N)
• 递归:α_t (j)=∑(i=1)^N▒〖a(t-1) (i)×a_ij×b_j (o_t ) 〗 (其中1≤j≤N,1≤t≤T)
• 终止:P(O│λ)=α_T (qF)=∑_(i=1)^N▒〖α_T (i)×α_i F〗
• 后向算法
• 后向算法与前向算法类似,它定义了一个概念叫后向概率:给定隐马尔科夫模型λ,定义在时刻t状态为q_i的条件下,从t+1到T的部分观测序列为o_(t+1),o_(t+2),…〖,o〗T的概率为后向概率,记为:
β t ( i ) = P ( o t + 1 , o t + 2 , . . . , o T ∣ i t = q i , λ ) \beta _{t}(i)=P(o_{t+1},o_{t+2},...,o_{T}\mid i_{t}=q_{i},\lambda ) βt(i)=P(ot+1,ot+2,...,oT∣it=qi,λ)
• 同样也可以用递推的方法求得后向概率β_t (i)及观测概率P(O│λ)。
• 解码问题:给定HMM情况下,给出观测序列,去寻找产生这个观测序列的最有可能的隐藏序列
• 动态规划算法
• Viterbi算法
• 维特比算法(Viterbi)是一个特殊但应用最广的动态规划算法,它是针对篱笆网络的有向图的最短路径问题而提出的。凡是使用隐含马尔可夫模型描述的问题都可以用维特比算法来解码,包括今天的数字通信、语音识别、机器翻译等。
• 步骤:
• 初始化
• 递归
• 终止
• 最优路径回溯
• 学习问题:根据已有的数据去学习HMM中的参数
• 监督式算法
• 观察序列和状态序列都给出,求HMM。
• 利用大数定理用频率来估算HMM的三种概率。
• 初始概率:(π_i ) ̂=(|q_i |)/(∑_i▒〖|q_i |〗)
• 转移概率:(a_ij ) ̂=(|q_ij |)/(∑(j=1)^N▒〖|q_ij |〗)
• 观测概率:(b_ij ) ̂=(|S_ik |)/(∑_(k=1)^M▒〖|q_ij |〗)
• 非监督式Baum-Welch算法
• 观察序列,没有给出状态序列,求HMM。
• 其实该算法的本质就是EM算法,因为它解决的问题就是:有了观测值X,而观测值有个隐变量Z时,求在HMM参数λ下的联合概率 P(X,Z|λ)。
• 求解步骤:
• 确定完全数据的对数似然函数
• EM算法E步:求Q函数Q(λ,λ ̂)
• EM算法M步:极大化Q函数求参数
HMM在语音识别中的应用
• EM算法E步:求Q函数Q(λ,λ ̂)
• EM算法M步:极大化Q函数求参数
• 对于输入语音,用Viterbi算法查出对应哪个HMM模型概率最大,由此得到最佳序列。
• 根据最佳序列对应组合出音素和单词。
• 根据语言模型形成词和句子。