控制教程 —— 巡航控制篇：2.PID控制器设计

系统模型及参数

前面教程已经得出了定速巡航系统的传递函数模型：
$$P(s)=\frac{V(s)}{U(s)}=\frac{1}{ms+b}[\frac{m/s}{N}]$$本教程采用的系统参数如下：
m 车辆质量 1000 kg
b 阻尼系数 50 N.s/m
u 额定控制力 500 N

控制性能目标

• 上升时间 < 5s
• 超调 < 10%
• 稳态误差 < 2%

PID概述

典型的反馈系统的框图如下所示：

回顾控制教程 —— 介绍篇：3.PID控制器设计，PID控制器的传递函数为：
$$C(s)=K_p+\frac{K_i}{s}+K_{d}s=\frac{K_d{s}^2+K_{p}s+K_i}{s}$$我们可以使用传递函数直接在MATLAB中定义PID控制器：

Kp = 1;
Ki = 1;
Kd = 1;

s = tf('s');
C = Kp + Ki/s + Kd*s

或者，我们可以使用MATLAB的pid控制器对象生成等效的连续时间控制器，如下所示：

C = pid(Kp,Ki,Kd)

比例控制

解决定速巡航的首要事情是找到添加比例控制($C=K_p$)的闭环传递函数。
通过简化单位反馈框图，带有比例控制器的闭环传递函数为：
$$T(s)=\frac{Y(s)}{R(s)}=\frac{P(s)C(s)}{1+P(s)C(s)}=\frac{K_p}{ms+b+K_p}$$
从控制教程 —— 介绍篇：3.PID控制器设计中可以得出，比例控制器 $K_p$ 可以减少上升时间。
现在，使用 $K_p=100$ 并给定参考速度为 $10m/s$。

m = 1000;
b = 50;
r = 10;

s = tf('s');
P_cruise = 1/(m*s + b);

Kp = 100;
C = pid(Kp);

T = feedback(C*P_cruise,1)

t = 0:0.1:20;
step(r*T,t)
axis([0 20 0 10])

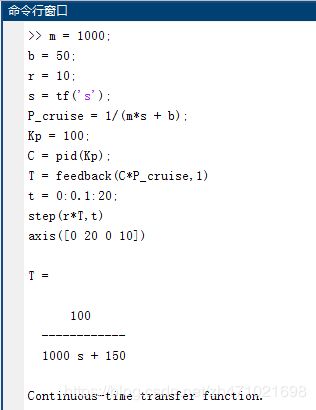
注意，我们已使用MATLAB的feedback命令简化闭环系统的框图，请亲自确认结果是否与上述推导的闭环传递函数T一致。
从图中可以看出，稳态误差和上升时间均未达到我们的设计标准。
您可以增加比例增益 $K_p$ 来减少上升时间和稳态误差。使 $K_p$ 等于5000，重新运行可以得到：

Kp = 5000;
C = pid(Kp);
T = feedback(C*P_cruise,1);

step(r*T,t)
axis([0 20 0 10])

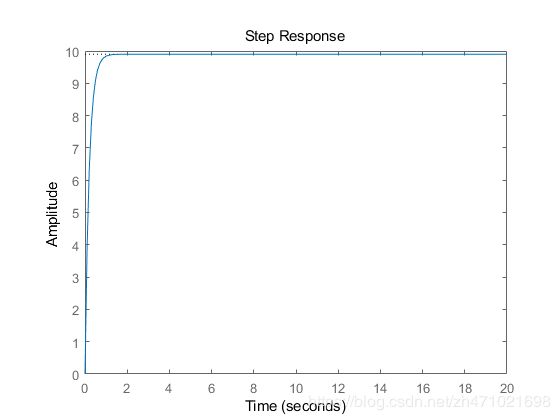
稳态误差现在基本上为0，并且上升时间已大大减少。然而，这种响应是不现实的，因为由于发动机和传动系统的功率限制，实际的巡航控制系统通常不能在不到0.5s 的时间内将车辆的速度从0改变到 10m/s。
在控制系统工程中，执行器限制在实践中经常遇到，因此，在提出新控制器时必须始终考虑所需的控制动作，我们将在后续教程中讨论该问题。
在这种情况下，该问题的解决方案是选择一个较低的比例增益 $K_p$ ，该比例增益将给出合理的上升时间，并添加一个积分控制器来消除稳态误差。

PI 控制器

具有PI控制器($C=K_p+K_i/s$)的巡航控制系统的闭环传递函数为：
$$T(s)=\frac{Y(s)}{R(s)}=\frac{P(s)C(s)}{1+P(s)C(s)}=\frac{K_{p}s+K_i}{m{s}^2+(b+K_p)s+K_i}$$从控制教程 —— 介绍篇：3.PID控制器设计中可以得出，系统中增加了一个积分控制器，从而消除了稳态误差。现在，让 $K_p$ 等于 600 和 $K_i$ 等于 1，看看响应发生了什么变化。

Kp = 600;
Ki = 1;
C = pid(Kp,Ki);

T = feedback(C*P_cruise,1);

step(r*T,t)
axis([0 20 0 10])

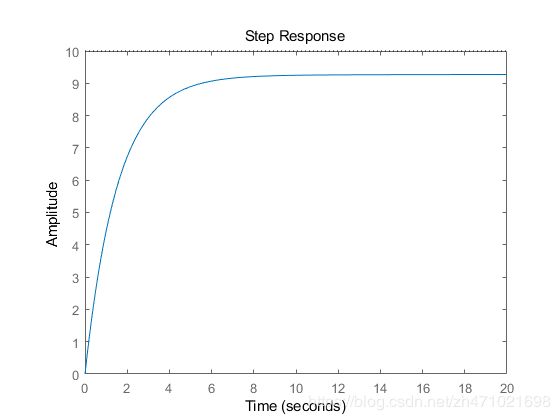
现在调整比例增益 $K_p$ 和积分增益 $K_i$ ，以获得所需的响应，调整积分增益 $K_i$ 时，建议您从一个较小的值开始，因为较大的 $K_i$ 可能会使响应不稳定。当$K_p$ 等于 800 而 $K_i$ 等于 40 时，阶跃响应将如下所示。

Kp = 800;
Ki = 40;
C = pid(Kp,Ki);

T = feedback(C*P_cruise,1);

step(r*T,t)
axis([0 20 0 10])

PID 控制器

在本示例中，不需要额外的微分控制器即可实现理想的性能，但是，您可能想了解加入微分控制器后的表现。具有PID控制器($C=K_p+K_i/s+K_{d}s$)的巡航控制系统的闭环传递函数为：
$$T(s)=\frac{Y(s)}{R(s)}=\frac{P(s)C(s)}{1+P(s)C(s)}=\frac{K_d{s}^2+K_{p}s+K_i}{(m+K_d)s^2+(b+K_p)s+K_i}$$假设 $K_p=1$，$K_i=1$，$K_d=1$，如下：

Kp = 1;
Ki = 1;
Kd = 1;
C = pid(Kp,Ki,Kd);

T = feedback(C*P_cruise,1);

绘制阶跃响应并调整所有 $K_p,K_i,K_d$，直到获得满意的结果。
建议，通常为满足所需要的性能需要反复调整PID控制器各项增益，解决这一繁琐过程的最佳方法是每次仅调整一个变量($K_p,K_i$或$K_d$)，并观察这种改变下响应的变化。控制教程 —— 介绍篇：3.PID控制器设计中已经描述了各项的特性。